Зміст
Вступ
Теоретична частина
1.1. Методика синтезу і дослідження аналогових фільтрів 1.2. Апроксимація АЧХ активних RC-фільтрів Баттервортівська апроксимація 1.3. Фільтри Бесселя 1.4. Еліптичні фільтри 1.5. Технічне завдання 2.Технічне завдання 2
2.1.Табличка істиності мультиплексора 16:1 2.2. Реалізація мультиплексора 16:1 на елементні базі Висновок
Вступ Електронні пристрої поділяються сьогодні на дві великі групи – аналогові і цифрові. Аналогові пристрої в своїй роботі використовують в основному неперервні сигнали, а цифрові пристрої сигнали, які мають перервну структуру, тобто мають імпульсну форму. Вони або є, або їх нема. На початку розвитку електроніки переважали аналогові пристрої, тому що на той час вони були більш швидкодіючими і мали менші габарити. В більшості своїй вони використовували для своєї реалізації електронні лампи, і тому знання їх роботи було необхідне спеціалісту з електронних схем. Поряд цим розроблялись схеми на лампах або реле, де уже використовувались цифрові сигнали, як правило в вигляді появи або відсутності напруги або струму на їх входах і виходах. З часом цифрові пристрої знаходили все більше застосувань, а їх елементна база все більш покращувалась. Спочатку почали використовувати транзистори, потім невеликі інтегральні схеми, а далі мікропроцесори, які дозволили сконструювати сучасні комп’ютери.
Крім того, різні підсилювачі, особливо потужні, потребують для своєї реалізації аналогових пристроїв. Також є застосування електронних пристроїв, де аналогові схеми будуть більш ефективними, чим цифрові. Наприклад, там, де необхідна велика швидкодія, а точність не має особливого значення. В зв’язку з розвитком як аналогових так цифрових пристроїв з’явилась необхідність в спеціальних навчальних наукових дисциплінах, яка б навчала ефективній розробці тих і інших схем. Тому від кваліфікації розробників цифрових схем – схемотехніків багато що залежить в ньому і, в першу чергу, його швидкодія і надійність.
СИНТЕЗ АНАЛОГОВИХ ФІЛЬТРІВ
З ВИКОРИСТАННЯМ СИСТЕМИ SCILAB
Мета: освоєння методики апроксимації АЧХ і ФЧХ, групового часу затримки аналогових фільтрів в частотній області з допомогою функцій системи SciLab
Теоретична частина
Пристрої фільтрації сигналів (фільтри) є одними з найбільш поширених і важливих компонент електронних схем, що використовуються для обробки сигналів. Фільтром називається пристрій, який реалізує необхідну залежність зміни параметрів сигналу (амплітуди, фазової і часової затримки) від частоти. Метою розробки фільтрів є знаходження алгоритму фільтрації сигналу у відповідності з задачею, для розв’язання якої призначений фільтр, вибір структури і параметрів пристрою, який реалізує такий фільтр. Процедура розробки фільтрів достатньо добре формалізована і піддається автоматизації. Підсистеми проектування фільтрів включають до складу сучасних систем автоматизованого проектування (САПР) електронних пристроїв. Але основною задачею таких систем є отримання готового пристрою, внутрішня структура якого недоступна розробнику. Це не дозволяє оцінити степінь оптимальності пропонованого системою проектного рішення, а також вияснити причини цілого ряду небажаних ефектів, які часто виникають при використанні пропонованих САПР пристроїв. По цій причині розробник повинен розуміти фізичні принципи, які реалізуються при побудові аналогових методів фільтрації сигналів і добре представляти собі технологію проектування відповідних фільтрів. Одним з потужних і надійних інструментів для розробки алгоритмів фільтрації сигналів і їх дослідження є пакет програм SciLab.
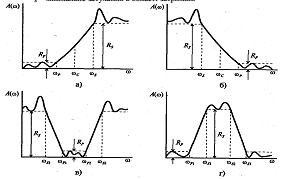
Рис. 1.1. Амплітудно - частотні характеристики: а) фільтра нижніх частот;
б) фільтра верхніх частот; в) смугового фільтра; г) режекторного фільтра
При
розробці фільтра необхідну характеристику
затухання апроксимують
деякими
передаточними функціями, АЧХ у яких
наближається до однієї з
ідеальних
характеристик. Така передаточна функція
характеризує стійку фізично
реалізовану
ланку фільтрації.
Математичні моделі
фільтрів. Математичною моделлю фільтра
є його
представлення в формі
деякої математичної функції або
рівняння. Від такої
моделі залежить
форма і спосіб реалізації фільтра і
можуть залежати його деякі
характеристики,
важливі для його реалізації. Тому
потрібно вміти переходити
від однієї
математичної моделі до іншої.
Найбільш
поширеною формою математичних моделей
фільтрів є їх представлення своїми
передаточними функціями (tf -
представлення). Для аналогових фільтрів
передаточна функція має вигляд:
де
1.1. Методика синтезу і дослідження аналогових фільтрів
Методика проектування аналогових фільтрів:
1) вибирається тип функції, що апроксимує частотну характеристикуфільтра (Баттервортівська,Чебишевська,Бесселівська і т.д.); 2) розраховується порядок ФНЧ - прототипу фільтра, його нулі, полюса і коефіцієнти передаточної функції; 3) виконується процедура частотного перетворення ФНЧ - прототипа в необхідний тип фільтра (ФНЧ-ФНЧ, ФНЧ-ФВЧ, ФНЧ-ПФ, ФНЧ-РФ); 4) передатна функція фільтра перетвориться до вигляду, зручного для його реалізації; 5) реалізація передаточної функції у вигляді електронної схеми активного RC-фільтра. Процедура синтезу електронних фільтрів включає декілька основних етапів. Першим етапом є апроксимація – процедура отримання передаточної функції,яка із заданою точністю відтворює задані частотні або часові характеристики. Передаточна функція, знайдена на етапі апроксимації, потім реалізується у вигляді електронної схеми активного RC-фільтра.
1.2 Апроксимація ачх активних rc-фільтрів Баттервортівська апроксимація:
Функція
Баттерворта - математична функція, яка
використовується для отримання
максимально гладкою АЧХ фільтру. АЧХ
фільтрів на основі функції Баттерворта,
не має пульсацій ні в смузі пропускання,
ні в смузі затримки. При фіксованому
порядку фільтри Баттерворта мають
найширшу перехідну смугу в порівнянні
з фільтрами, які використовують інші
апроксимуючі функції. Цей пристрій
одержав дуже широке поширення. Фільтр
має АЧХ, яка в середині смуги пропускання
дуже близька до плоскої і дещо закруглюється
в околі частоти зрізу. За межами смуги
пропускання швидкість загасання
збільшується і в деяких випадках досягає
6n децибел на октаву, де n - порядок фільтра.
Передаточна функція фільтра має
вигляд:
Баттервортівські
фільтри мають частотну характеристику,
яка описується
функцією:
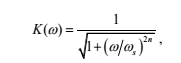де
ωr – частота зрізу фільтра, n – ціле
число, яке отримало назву порядку
фільтра.
Передаточна функція фільтра
нижніх частот n-го порядку
з
баттервортівською апроксимацією
описується виразом:
Амплітудо-частотна
характеристика баттервортівського
фільтра має
властивості:
- при довільному порядку n
-
при частоті зрізу ωp
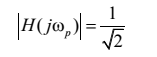
Коефіцієнт
передачі фільтра на нульовій частоті
дорівнює 1, на частоті зрізу≈ 0,707 =-3
дБ незалежно від порядку фільтра.
АЧХ такого фільтра є
максимально
плоскою при ω = 0 і ω → ∞ і монотонно
спадає від 1 до 0 зізростанням частоти
ω. На рис. Показані графіки
амплітудо-частотних
характеристик
фільтрів Баттерворта 3 та 5 порядків.
Очевидно, що чим більше порядок фільтра,
тим точніше апроксимується АЧХ ідеального
ФНЧ.
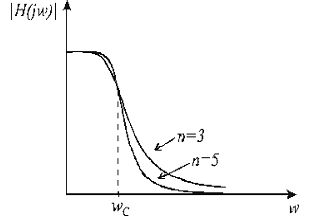Вигляд
АЧХ баттервортівського фільтра для
різних порядків n.
Порядок передаточної
функції визначається наближеною
формулою:
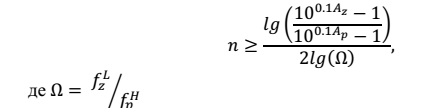
1.3. Фільтри Бесселя
Особливістю фільтрів Баттерворта і Чебишева є те, що спектральні складові вхідного сигналу при проходженні через них відчувають різну часову затримку.
Зміна часу затримки в середині смуги пропускання фільтра називається спотворенням, обумовленим затримкою сигналу. Таке спотворення збільшується зі зростанням порядку фільтра та рівня пульсацій. Якщо вхідний сигнал не є синусоїдальний, а містить коливання з кратними частотами, то через різні часові
затримки цих коливань фільтром форма вихідного сигналу спотворюється.
Існують фільтри, які всередині смуги пропускання забезпечують по стійну затримку для всіх спектральних складових сигналу. Але в цьому випадку характер зміни затухання в області частоти зрізу АЧХ сильно відрізняється від форми АЧХ фільтрів Чебишева і Баттерворта. У межах однієї з двох октав за частотою зрізу загасання змінюється дещо повільніше, ніж у інших типів фільтрів. Такі пристрої називаються фільтрами Бесселя. Вони застосовуються
головним чином у тих випадках, коли важливіше передати сигнал без спотворень.
Функція Бесселя - математична функція, яка використовується для
отримання найбільш лінійної ФЧХ фільтра без врахування вимог до АЧХ.
Фільтри, спроектовані на основі функцій Бесселя, мають майже постійний час
групової затримки. Але у таких фільтрів при перетворенні ФНЧ в ФВЧ, СФ або
РФ постійність часу затримки всередині смуги пропускання не зберігається.