
- •Завдання на екзамен з предмету “Диференціальні рівн’яння’’ Теоретичні завдання
- •Практичні завдання
- •1.Загальні поняття та означення диференціальних рівнянь першого порядку
- •2.Теорема Коші
- •3. Рівняння, що зводяться до рівнянь зі змінними, що розділяються.
- •4. Однорідні диференціальні рівняння. Загальні поняття.
- •5. Рівняння, що зводяться до однорідних
- •6. Лінійні диференціальні рівняння першого порядку
- •7. Рівняння Бернуллі
- •8. Рівняння Рікатті
- •9. Рівняння в повних диференціалах
- •10. Інтегруючий множник
- •11. Частинні випадки інтегруючих множників
- •15. Рівняння Лагранжа
- •16. Рівняння Клеро
- •17. Диференціальні рівняння вищих порядків
- •18. Задача Коші для диференціальних рівнянь вищих порядків.
- •19. Теорема Коші
- •20. Загальний розв’язок диференціальних рівнянь вищих порядків
- •21. Частинний розв’язок диференціальних рівнянь вищих порядків.
Завдання на екзамен з предмету “Диференціальні рівн’яння’’ Теоретичні завдання
Загальні поняття та означення диференціального рівняння першого порядку.
Теорема Коші (про існування та єдиність розв’язків).
Рівняння, що зводяться до рівнянь зі змінними, що розділяються.
Однорідні диференціальні рівняння.
Рівняння, що зводяться до однорідних.
Лінійні рівняння першого порядку
Рівняння Бернуллі
Рівняння Рікатті
Рівняння в повних диференціалах
Інтегруючий множник
Частинні випадки інтегруючих множників
Частинні випадки рівнянь, що інтегруються в квадратурах (F(у´)=0;
Частинні випадки рівнянь, що інтегруються в квадратурах F(х,у´)=0).
Частинні випадки рівнянь, що інтегруються в квадратурах (F(у,у´)=0).
Рівняння Лагранжа
Рівняння Клеро
Диференціальні рівняння вищих порядків.
Задача Коші для диференціальних рівнянь вищих порядків.
Теорема Коші
Загальний розв’язок диференціальних рівнянь вищих порядків
Частинний розв’язок диференціальних рівнянь вищих порядків.
Диференціальні рівняння вищих порядків, що інтегруються в квадратурах, виду: у(п)=f(x)
Диференціальні рівняння вищих порядків, що інтегруються в квадратурах, виду: F(x, у(п))=0
Диференціальні рівняння вищих порядків, що інтегруються в квадратурах, виду:
F(у(п-1), у(п))=0
Практичні завдання
Знайти загальний розв’язок рівняння
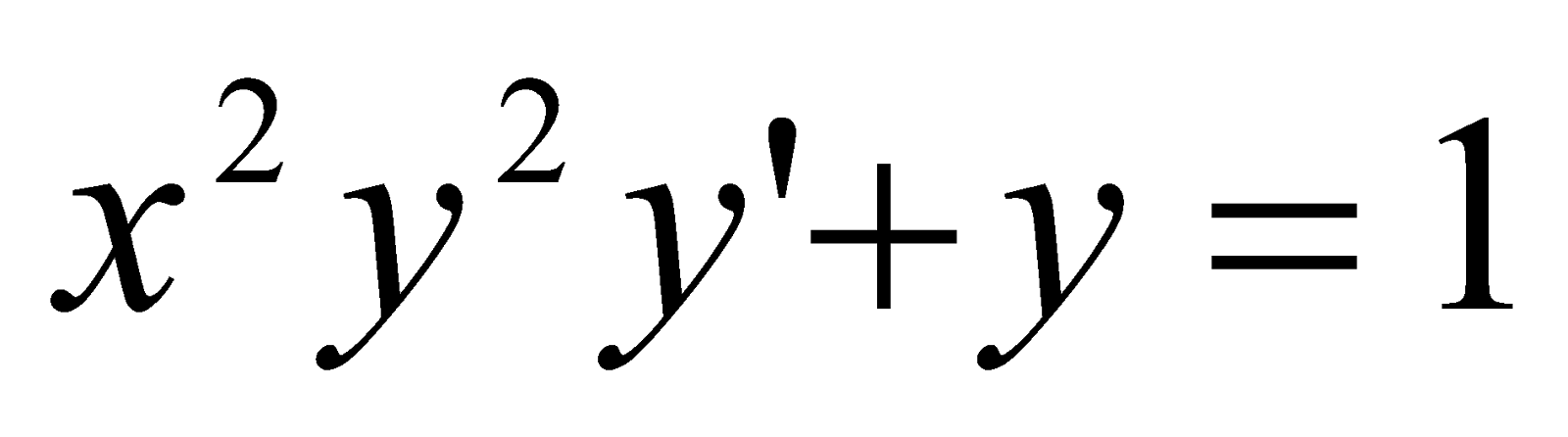 ;
;Знайти загальний розв’язок рівняння
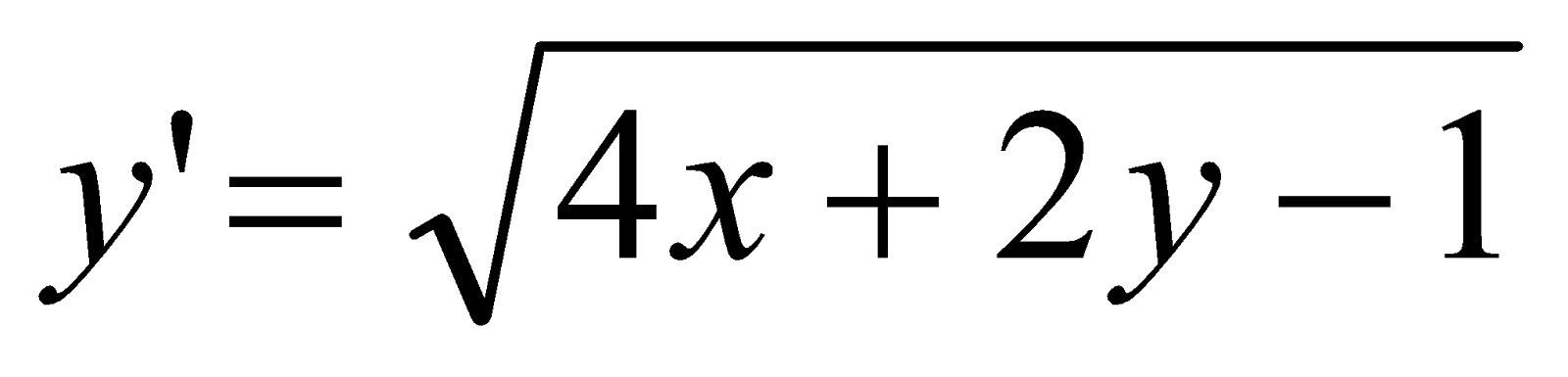 .;
.;Знайти загальний розв’язок рівняння
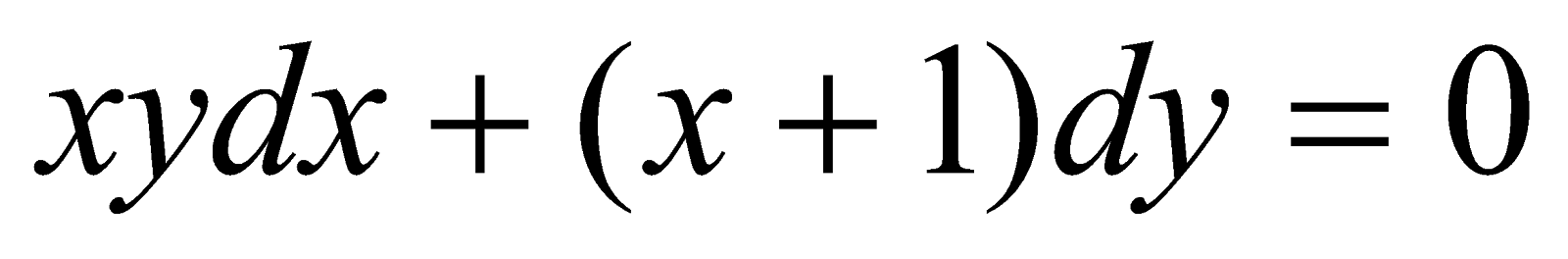 ;
;Знайти загальний розв’язок рівняння
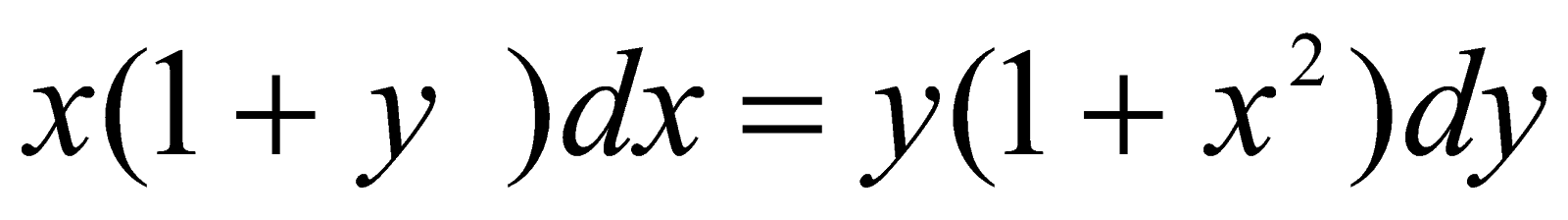 ;
;Знайти частинні розв’язки, що задовольняють заданим умовам:
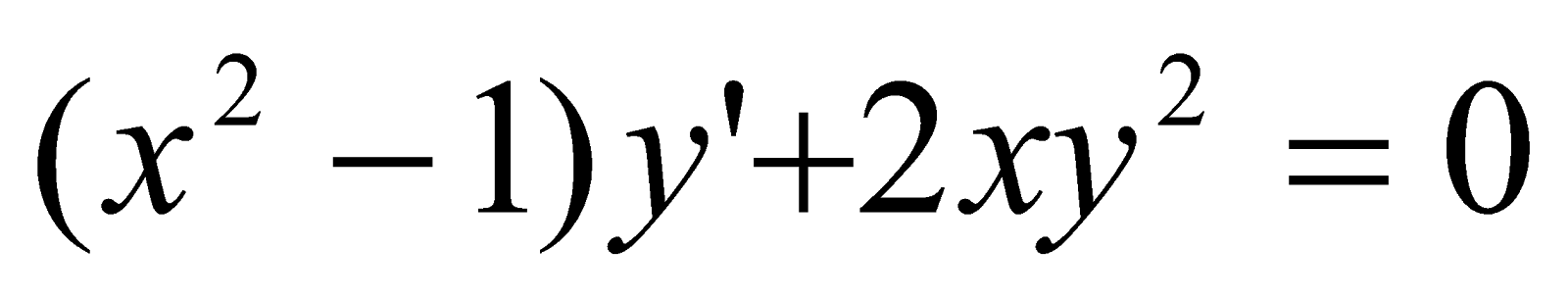 ,
,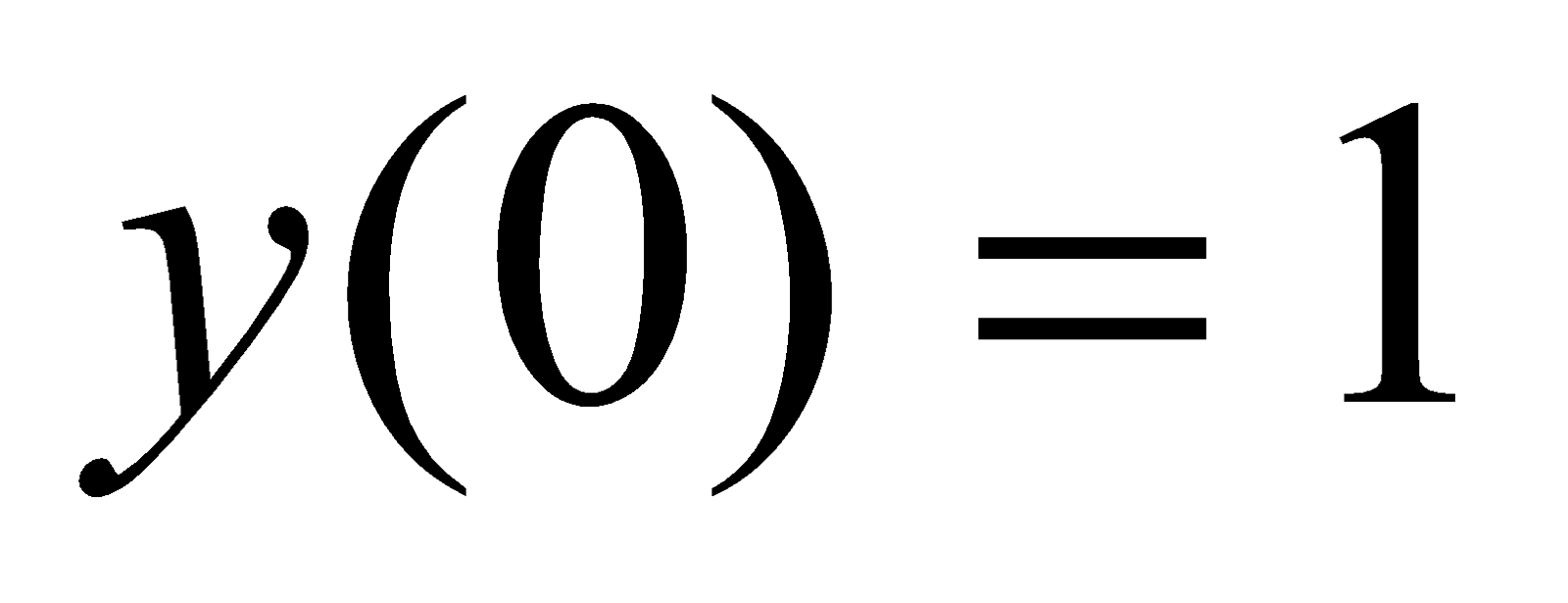 ;
;Знайти частинні розв’язки, що задовольняють заданим умовам: dx=(2y2+5)dy, y(0)=2;
Знайти частинні розв’язки, що задовольняють заданим умовам:
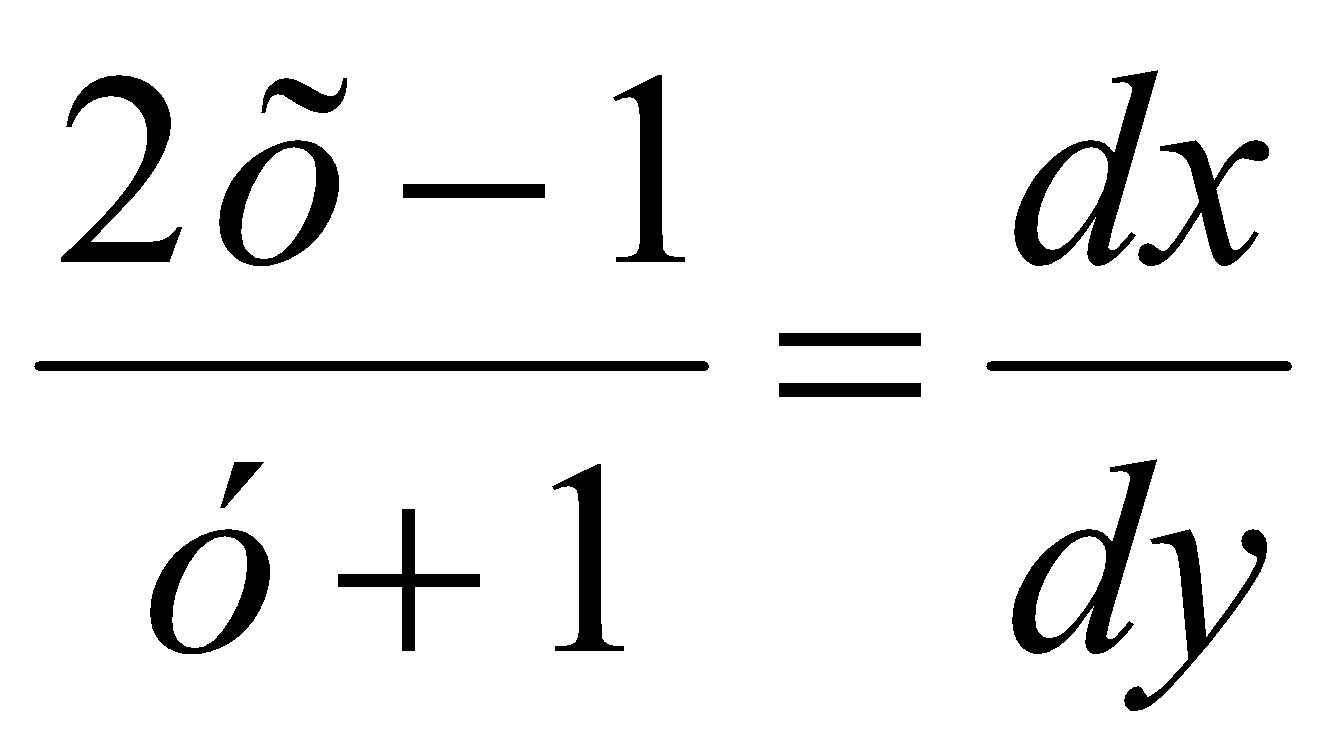 ;
y(5)=0;
;
y(5)=0;Знайти частинні розв’язки, що задовольняють заданим умовам: dy=(3x-7)dx, y(1)=0;
Розв’язати рівняння
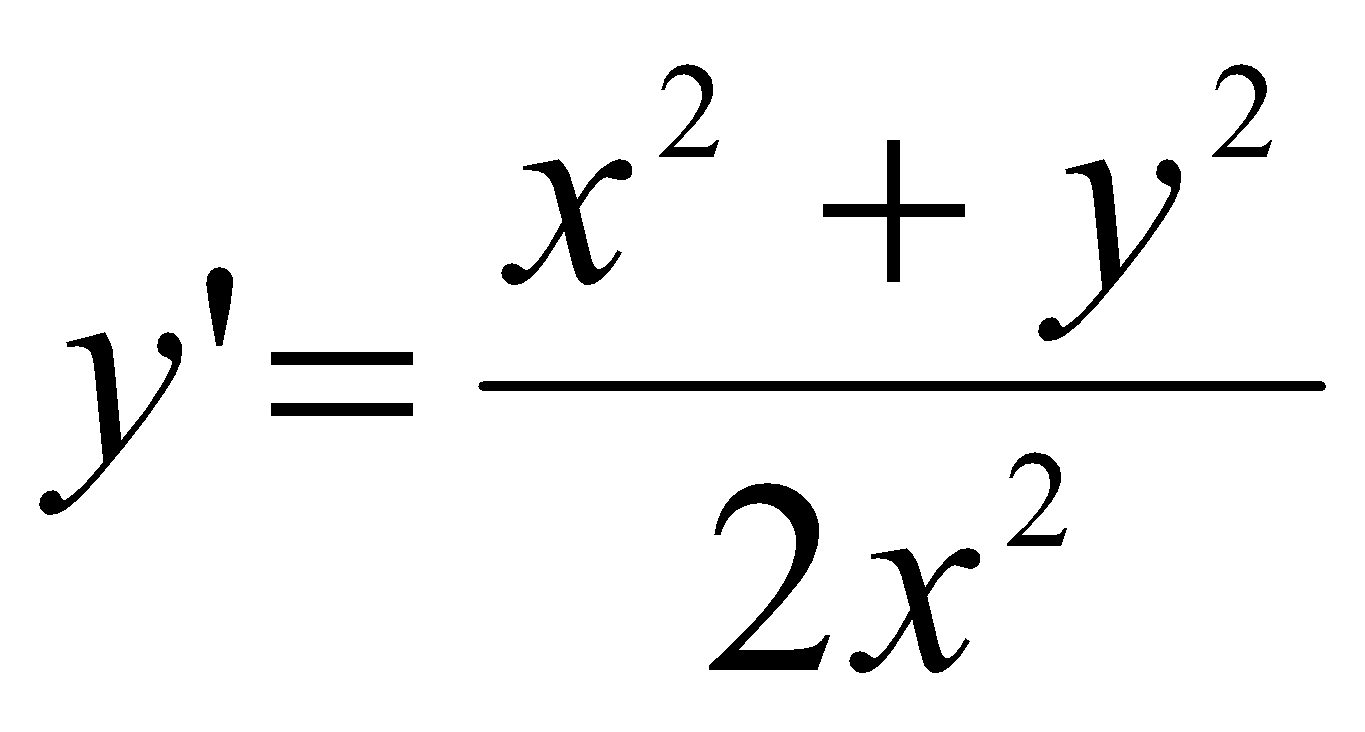 ;
;Розв’язати рівняння
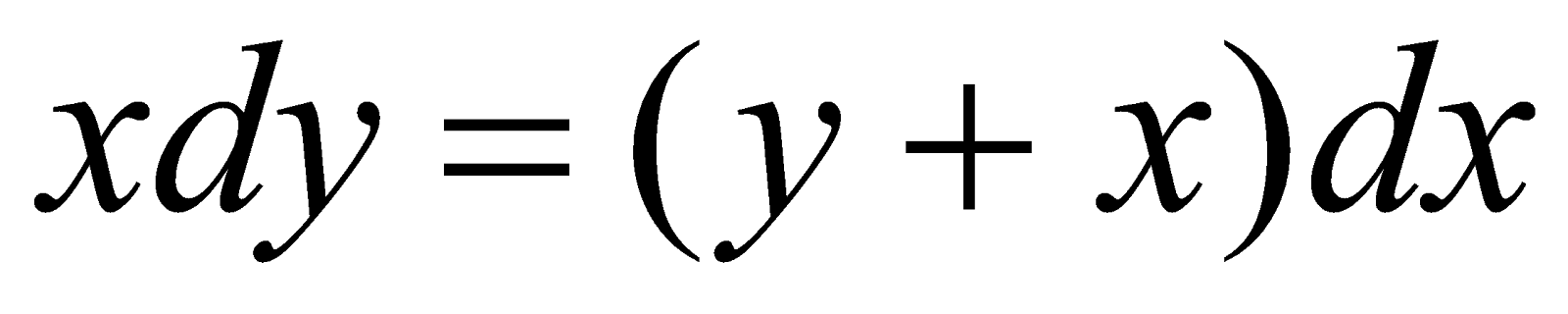 ;
;Розв’язати рівняння
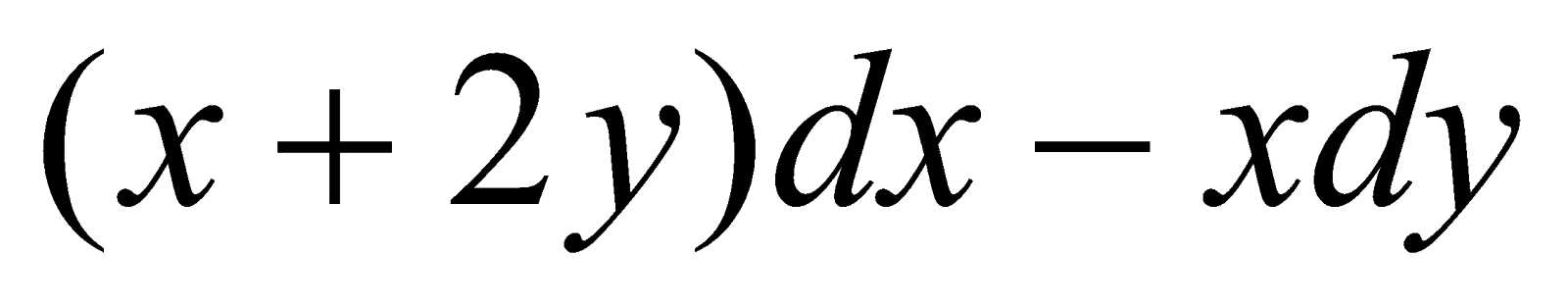 ;
;Розв’язати рівняння
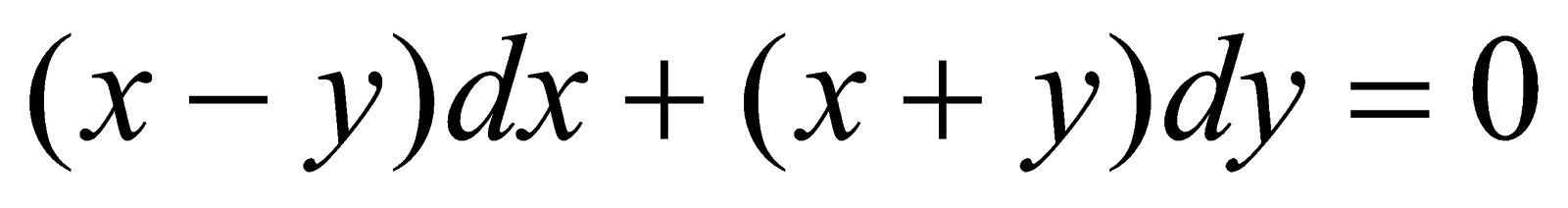 ;
;Розв’язати рівняння
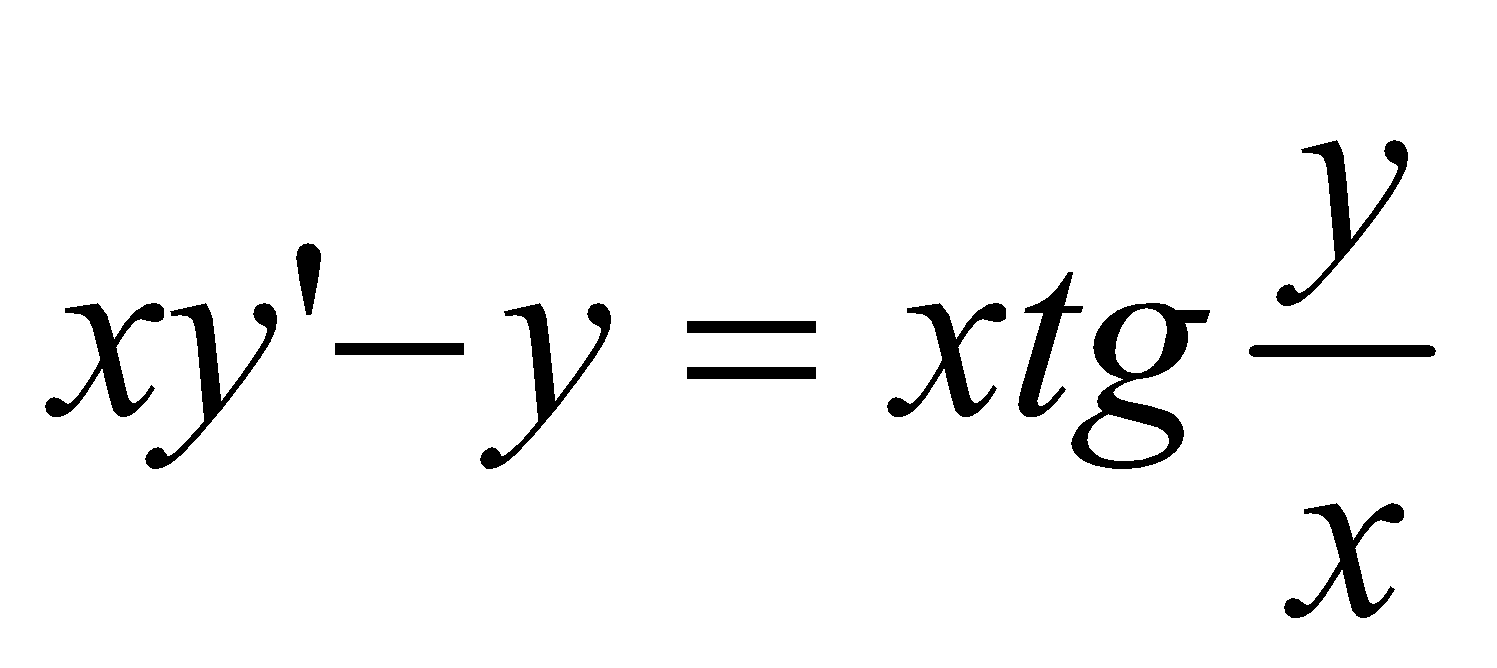 ;
;Розв’язати рівняння
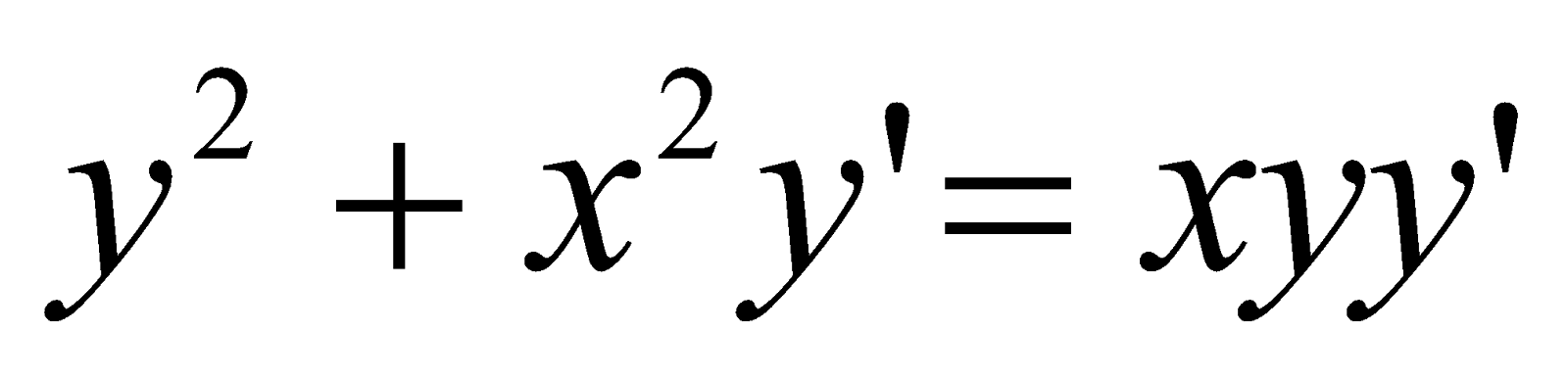 ;
;Розв’язати рівняння
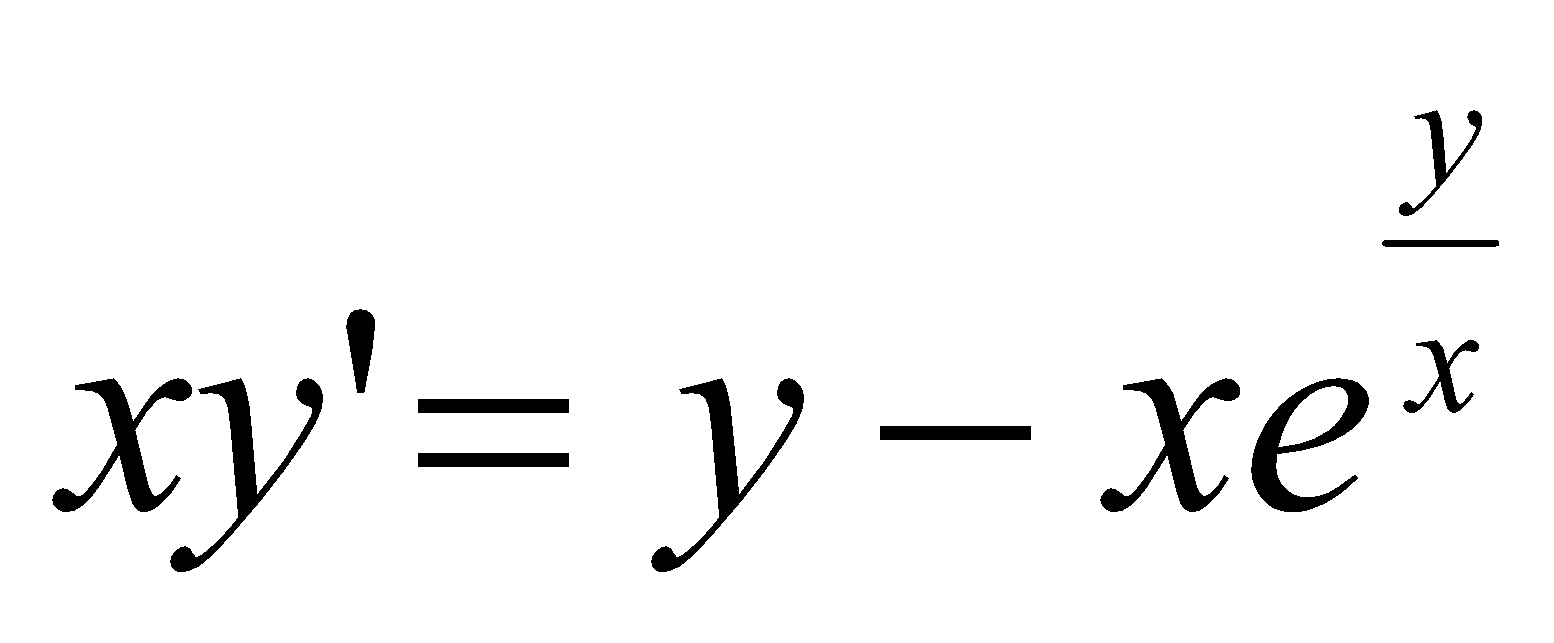 ;
;Знайти загальний розв’язок рівняння
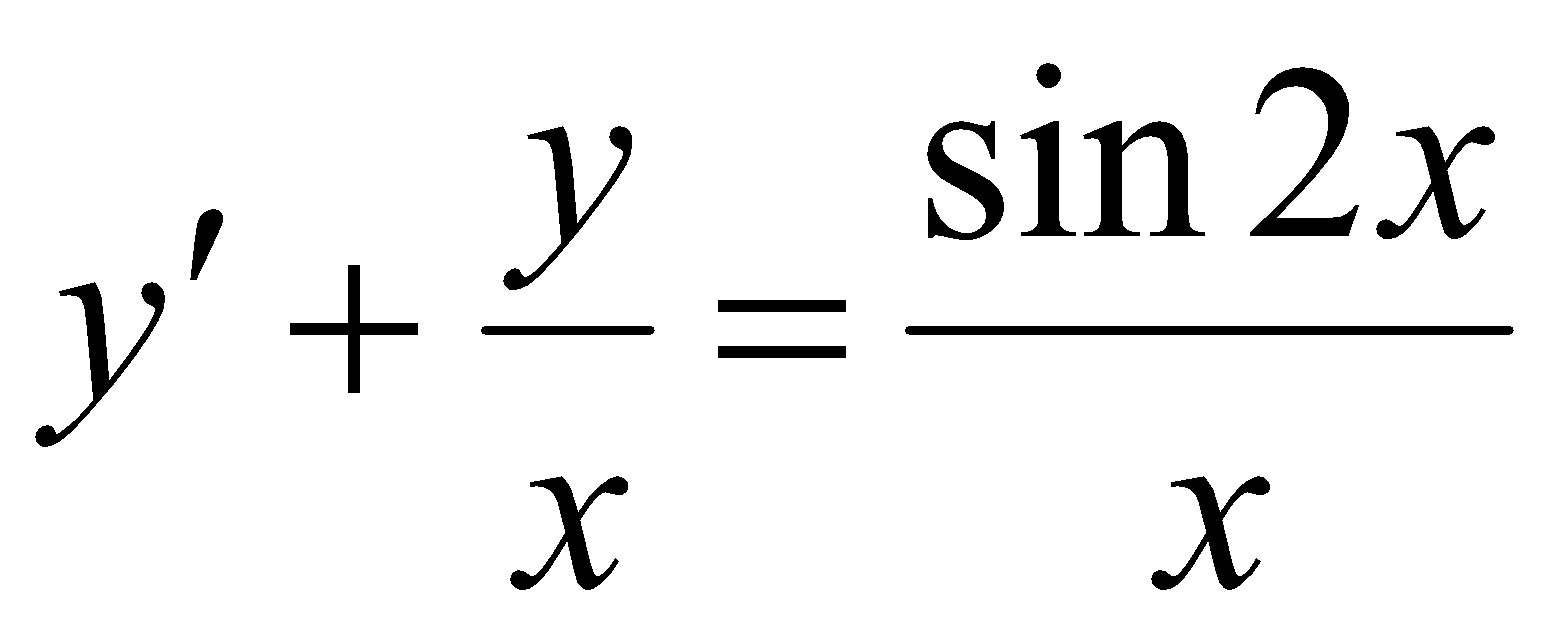 ;
;Розв’язати рівняння (х2 lny-x)y´-y=0;
Розв’язати рівняння
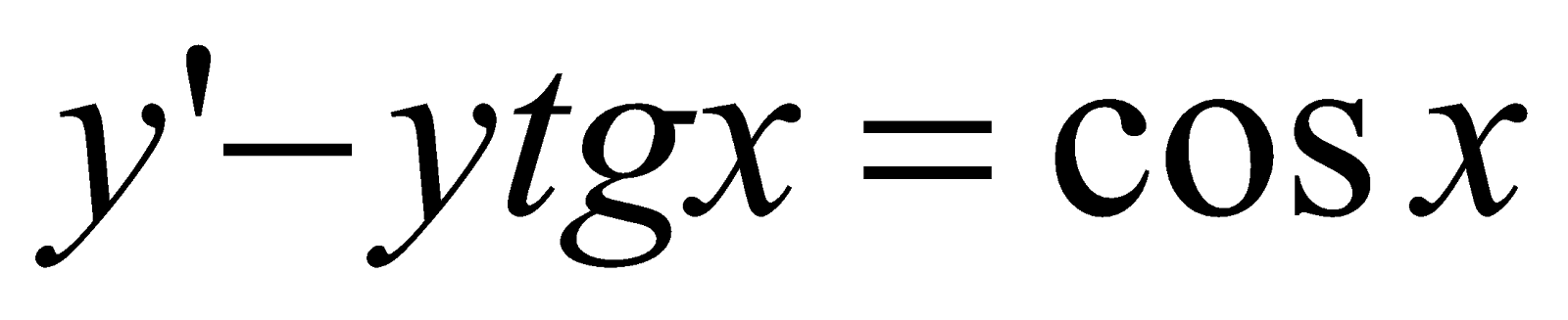 ;
;Розв’язати рівняння
 ;
;Розв’язати рівняння xy´+2y=x2
Розв’язати рівняння
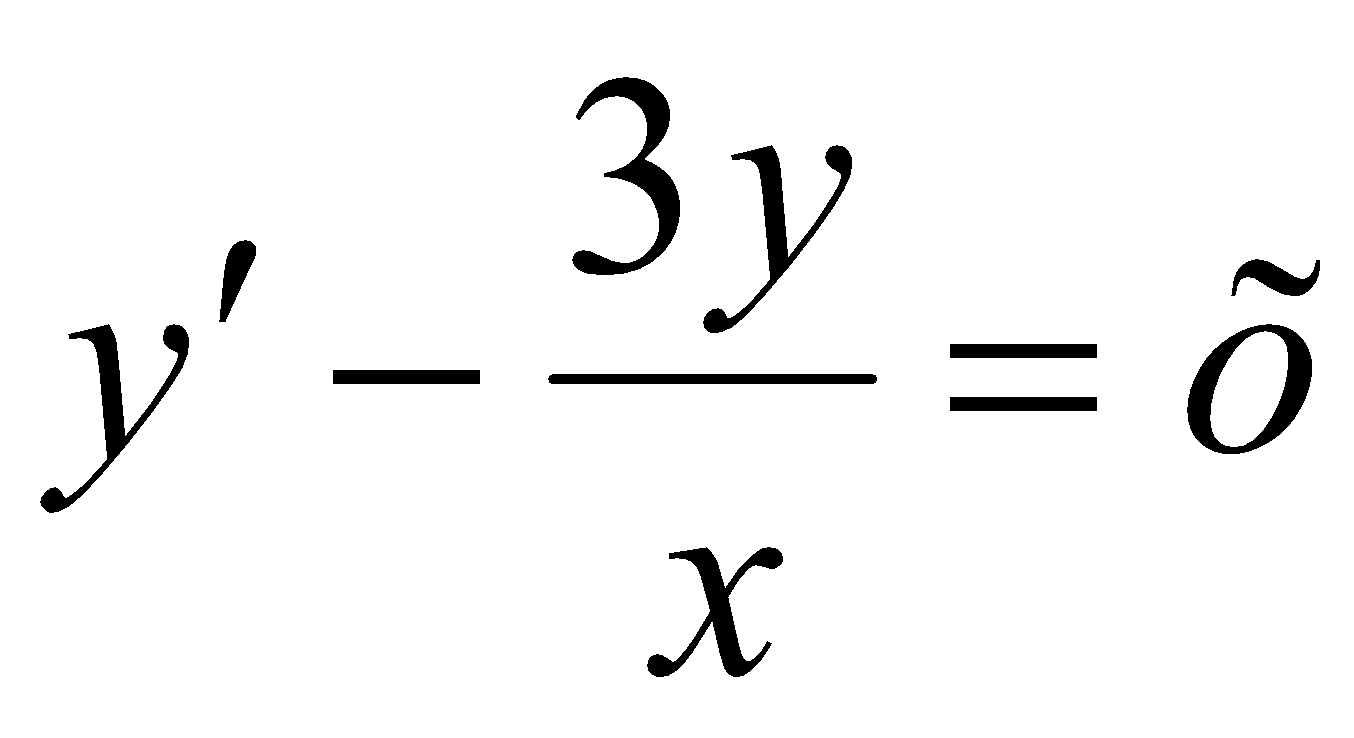 ;
;Розв’язати рівняння
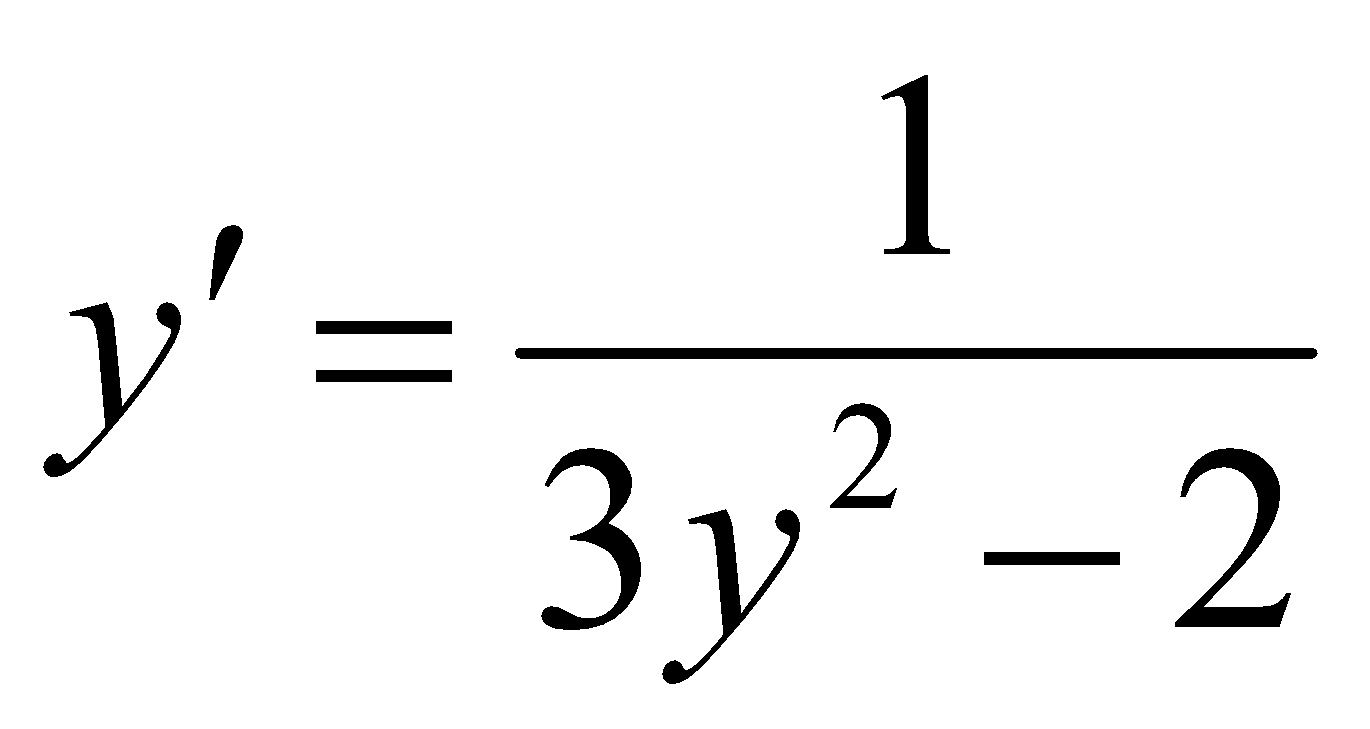 ;
;Розв’язати рівняння
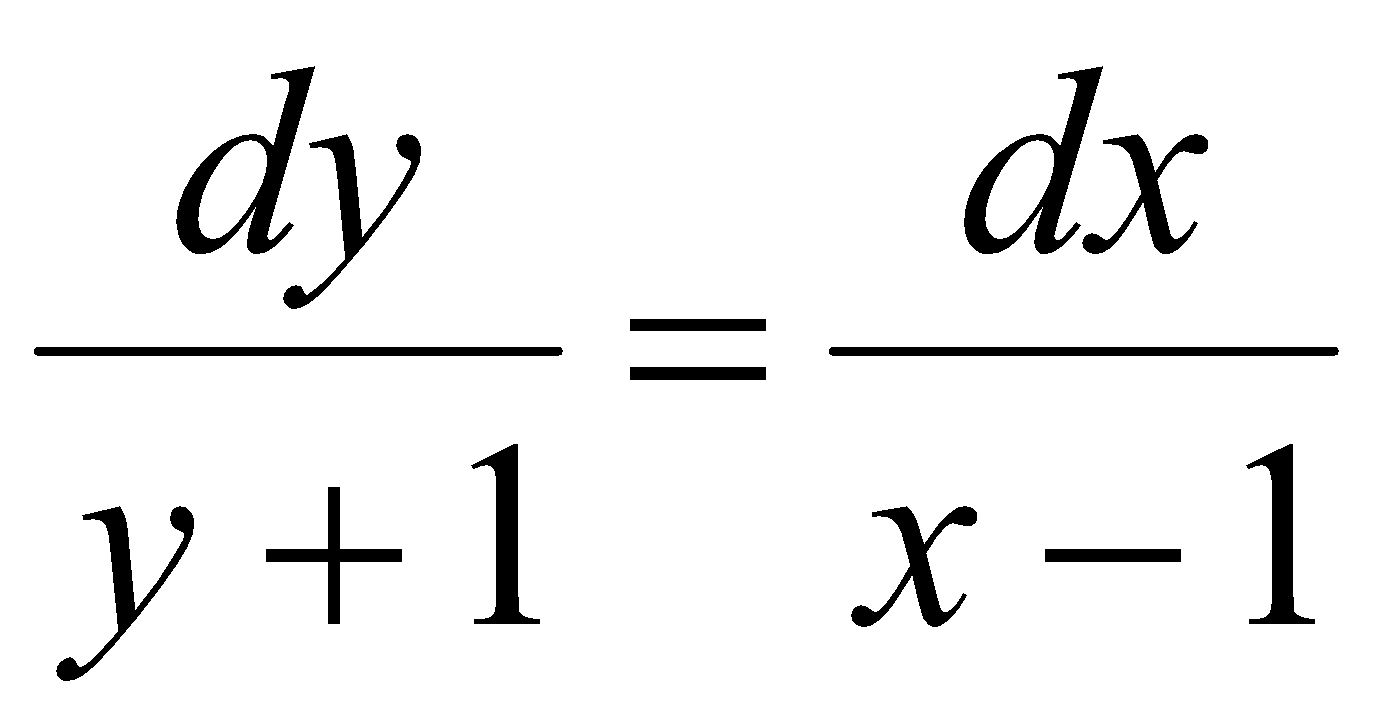 ;
;Розв’язати рівняння y´=2x;
Знайти загальний розв’язок рівняння
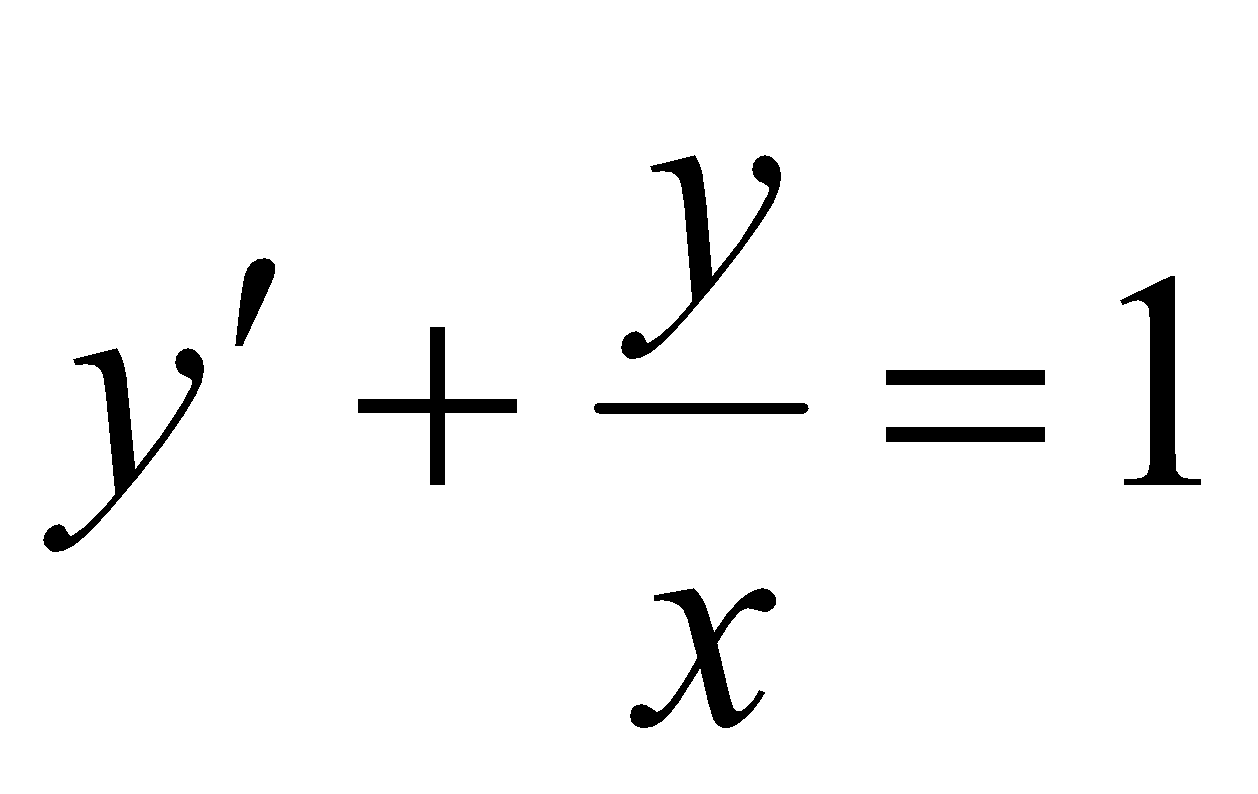 ;
;Знайти загальний розв’язок рівняння
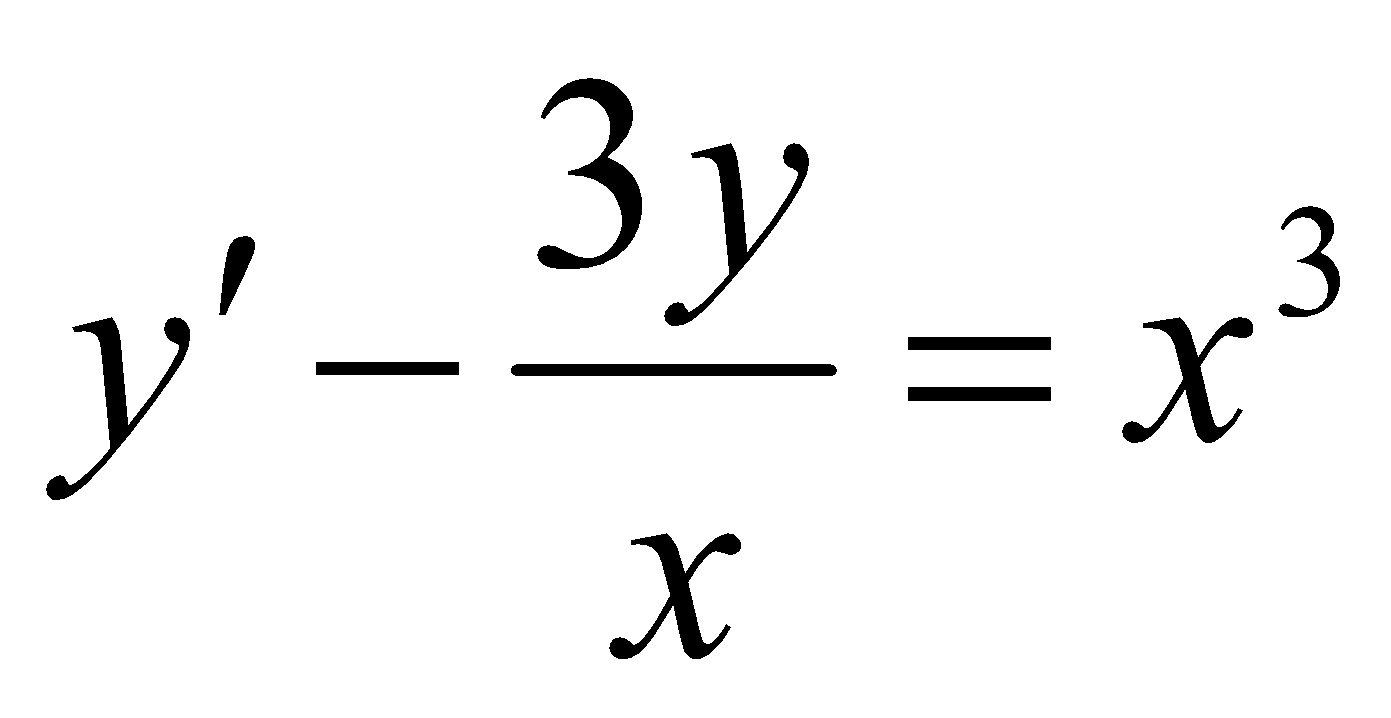 ;
;Знайти загальний розв’язок рівняння
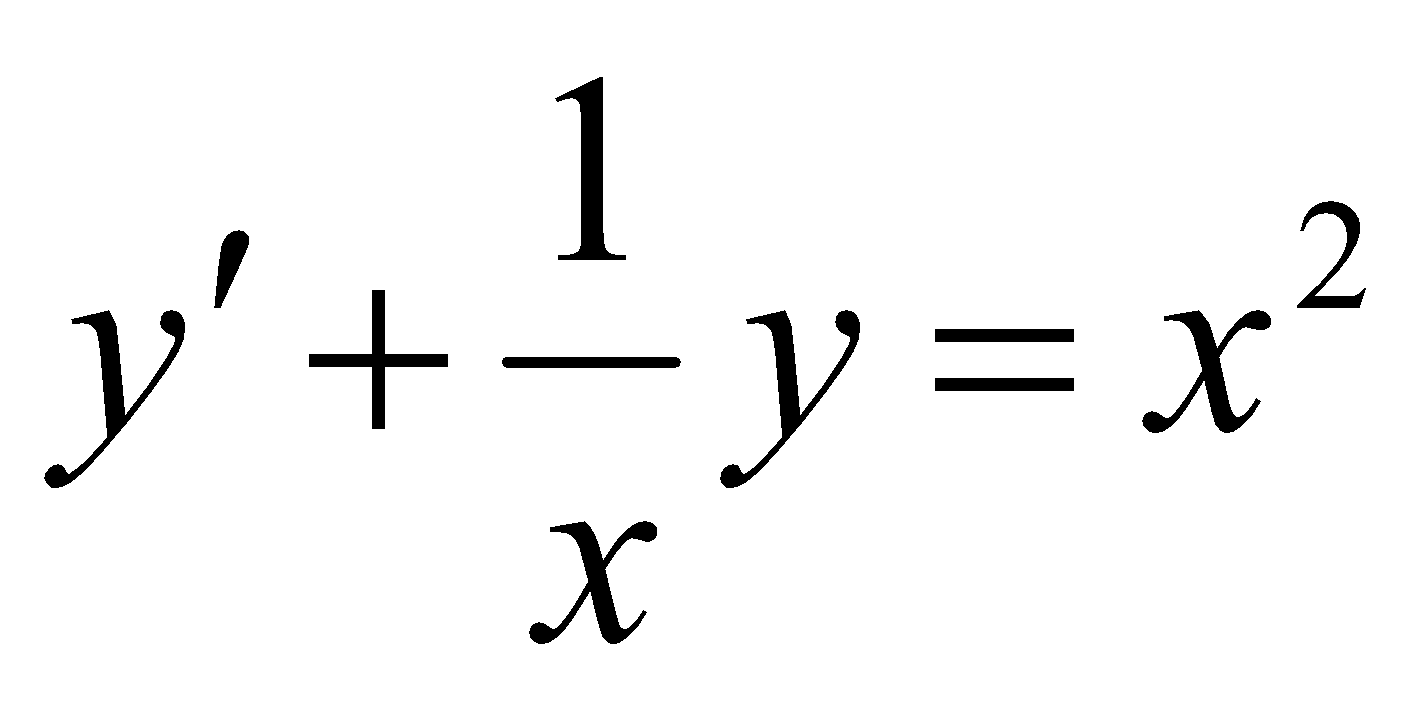 ;
;Перевірити чи задовольняє дане диференціальне рівняння вказану функцію
у''=х2+у2,
у=![]() ;
;
Перевірити чи задовольняє дане диференціальне рівняння вказану функцію
у''+у=0, у=cosx;
Перевірити чи задовольняє дане диференціальне рівняння вказану функцію
ху'+у=у2,
у=![]() ;
;
Розв’язати рівняння (3у2+2ху+2х)dx+(6ху+х2+3)dy=0;
Розв’язати рівняння (2ху+3х2у)dx+(х3-3у2)dy=0;
Розв’язати рівняння
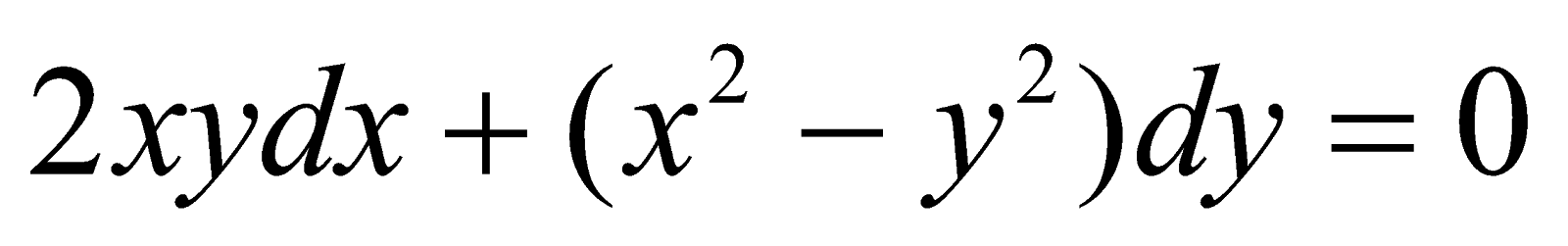 ;
;Розв’язати рівняння (х3+3ху2) dx+(у3 +3х2 у) dy=0;
Розв’язати рівняння
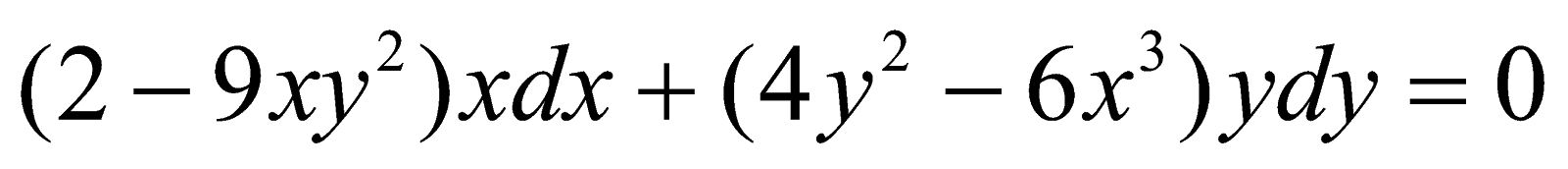 ;
;Розв’язати рівняння (хеу+ех) у'+еу+уех =0;
Розв’язати рівняння уху-1dx+хуlnxdy=0;
Розв’язати рівняння (2ху+arcsinx) dx +(arctgy+x2+1)dy=0;
Розв’язати рівняння y2 -1+(2xy+3y)y'=0;
Розв’язати рівняння y'''sin4 x= sin2x;
Розв’язати рівняння (x+ln y)=(1+
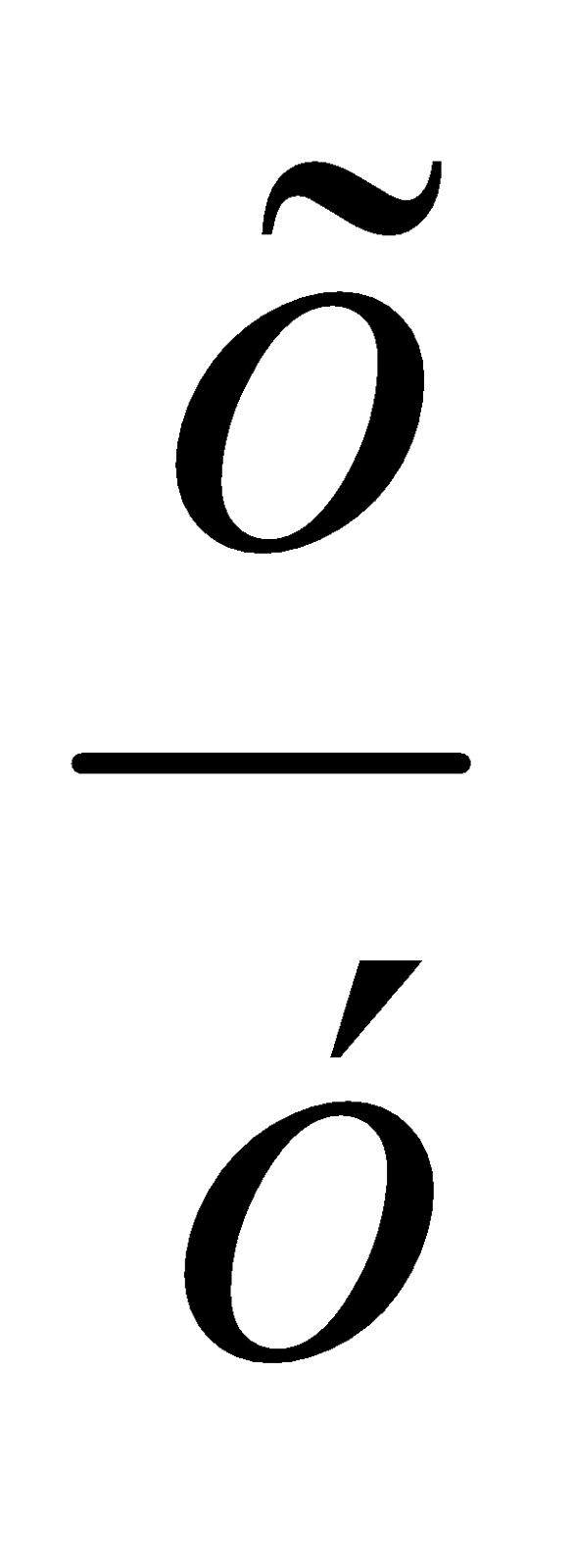 +siny)
y';
+siny)
y';Розв’язати рівняння (y')3 + (y')2+ y'-3=0
Розв’язати рівняння
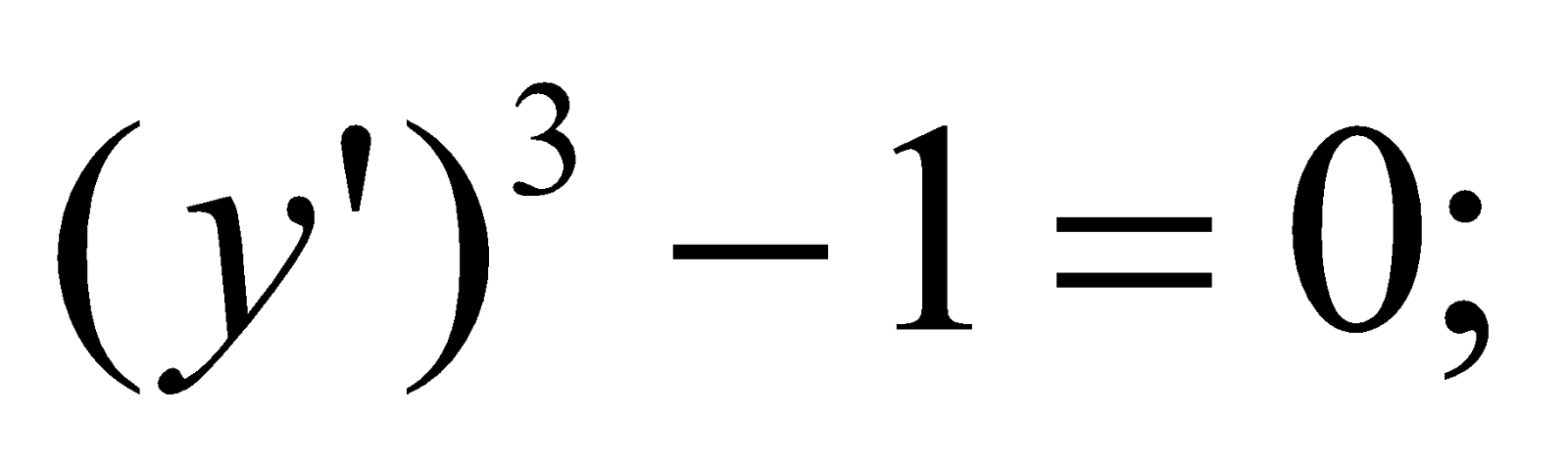
Розв’язати рівняння
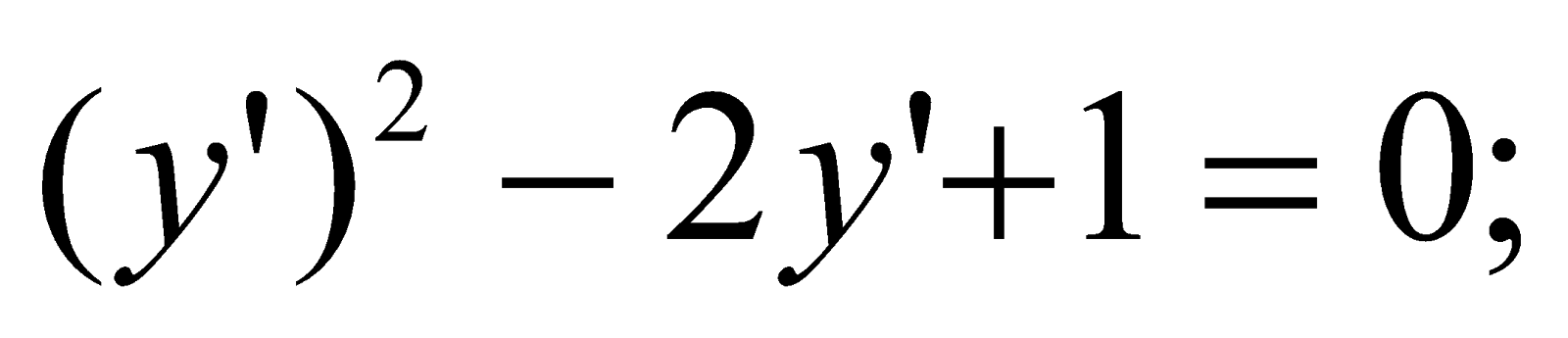
Розв’язати рівняння
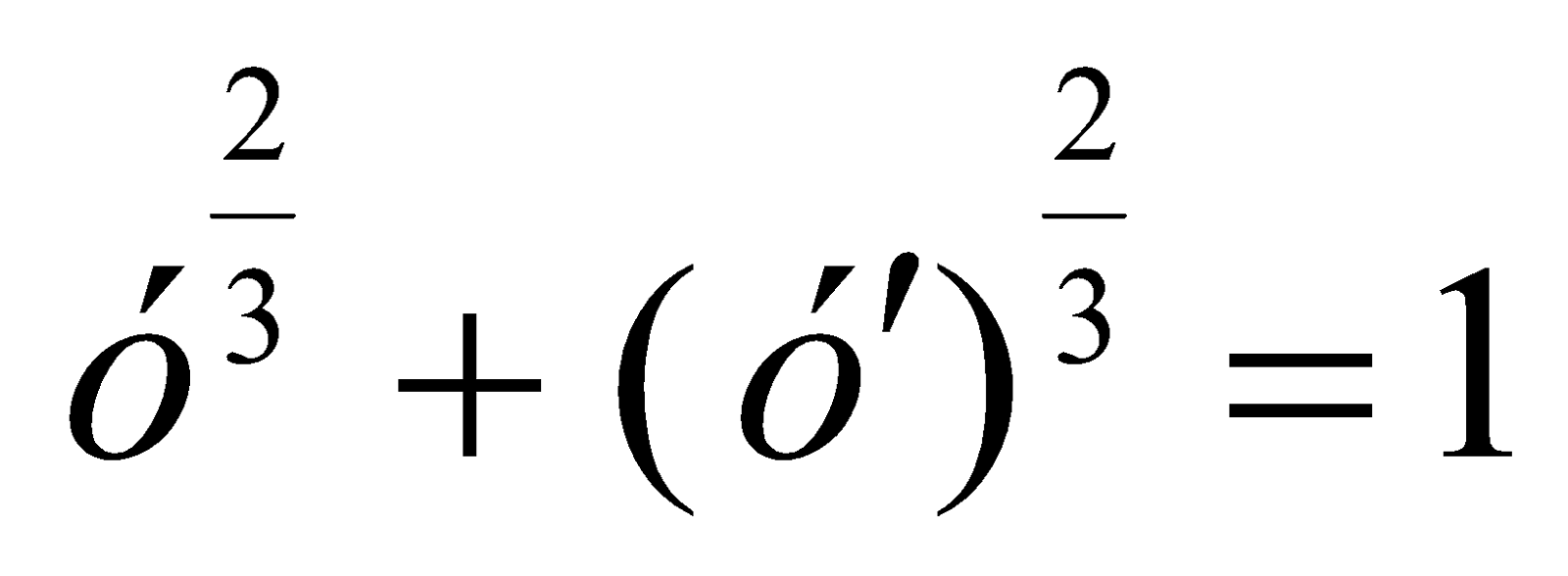
Розв’язати рівняння y=xy'-(y')2
Розв’язати рівняння
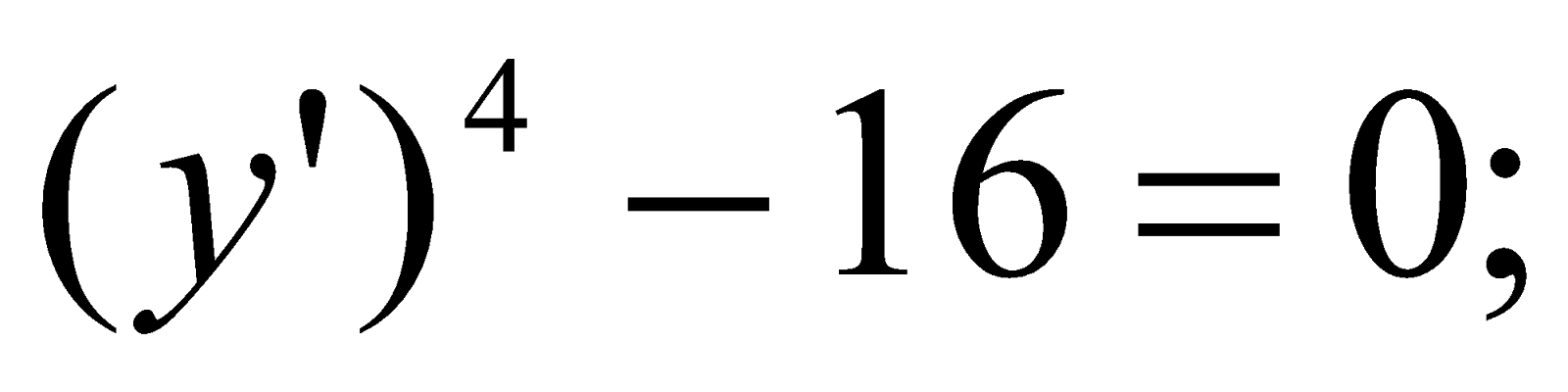
Розв’язати рівняння x=y'+(y')3
Розв’язати рівняння y' (x-ln y')=1;
Розв’язати рівняння y'''=e-5x;
Розв’язати рівняння
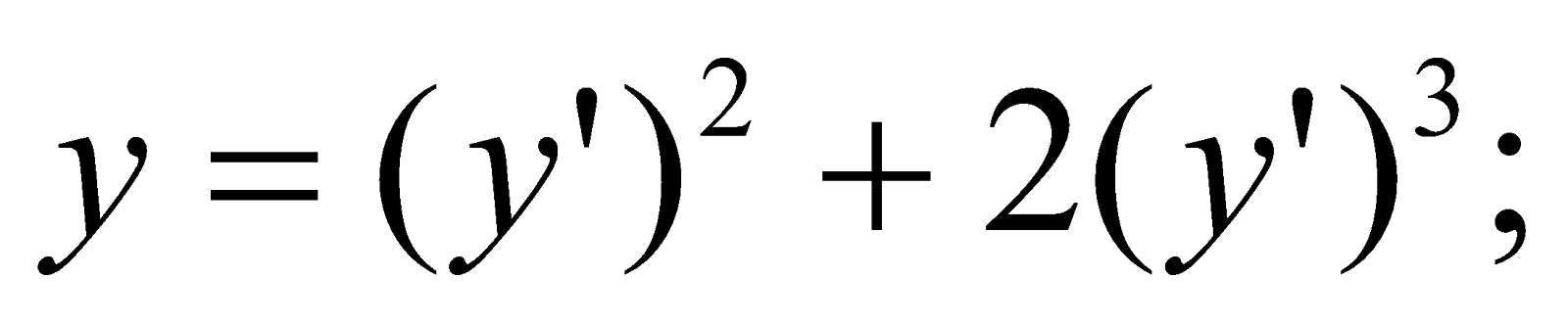
Розв’язати рівняння
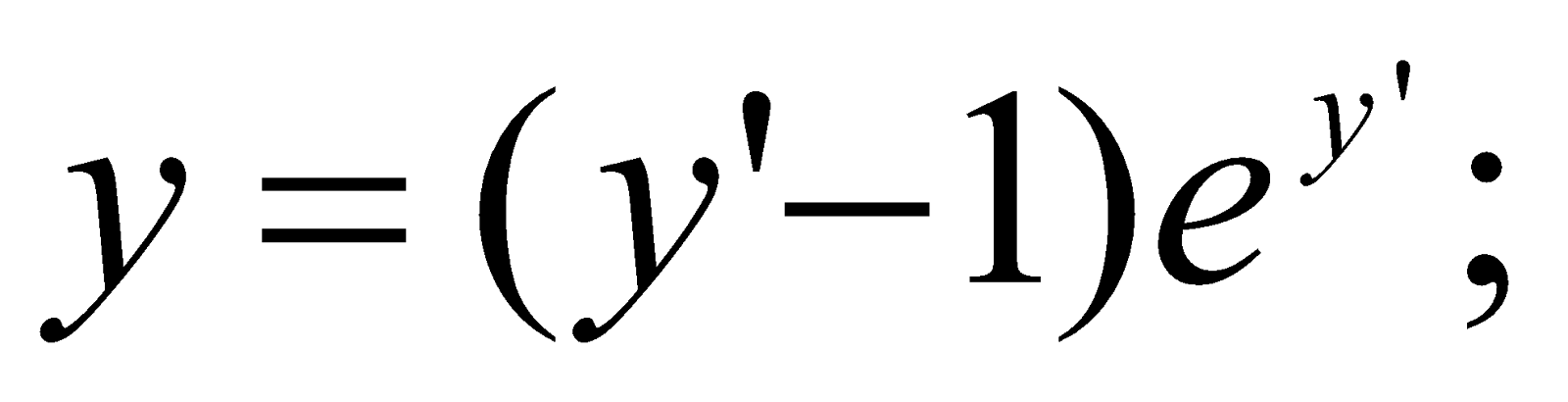
Розв’язати рівняння 2xy+3y=
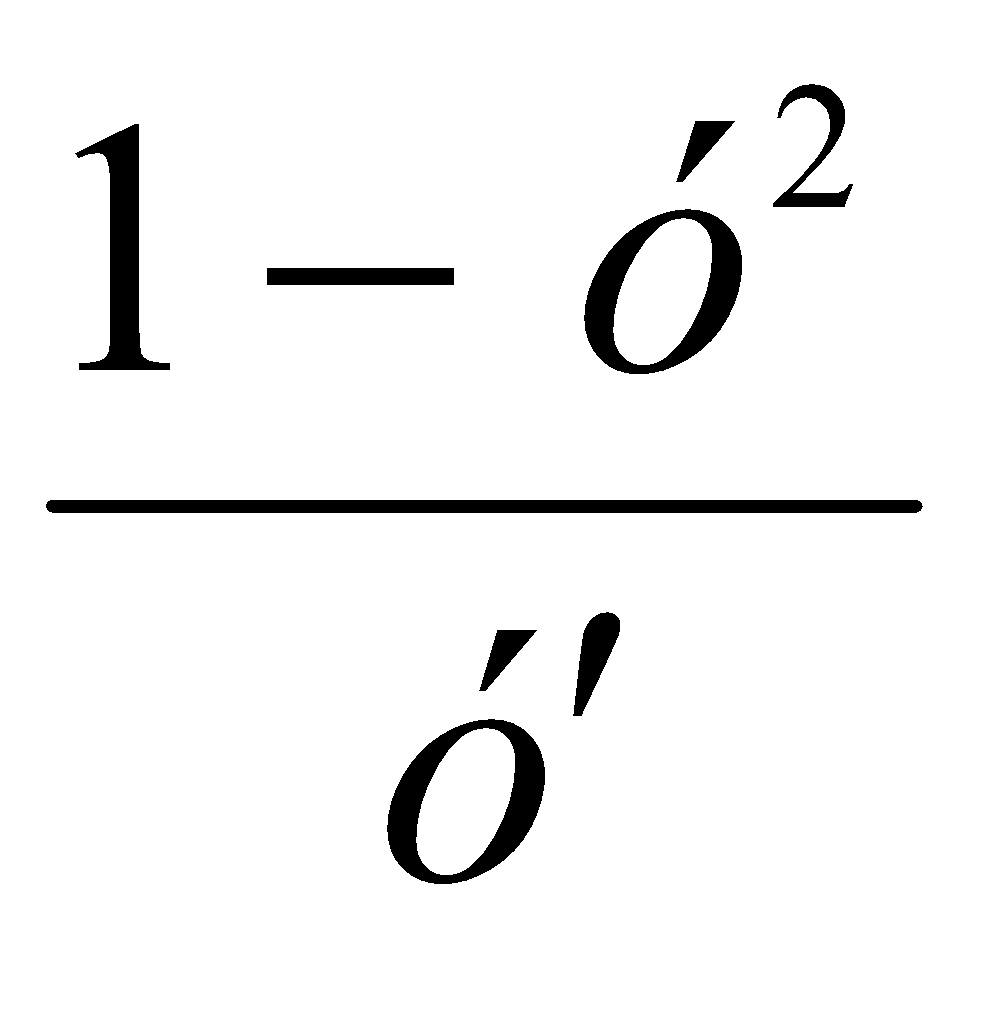 ;
;Розв’язати рівняння
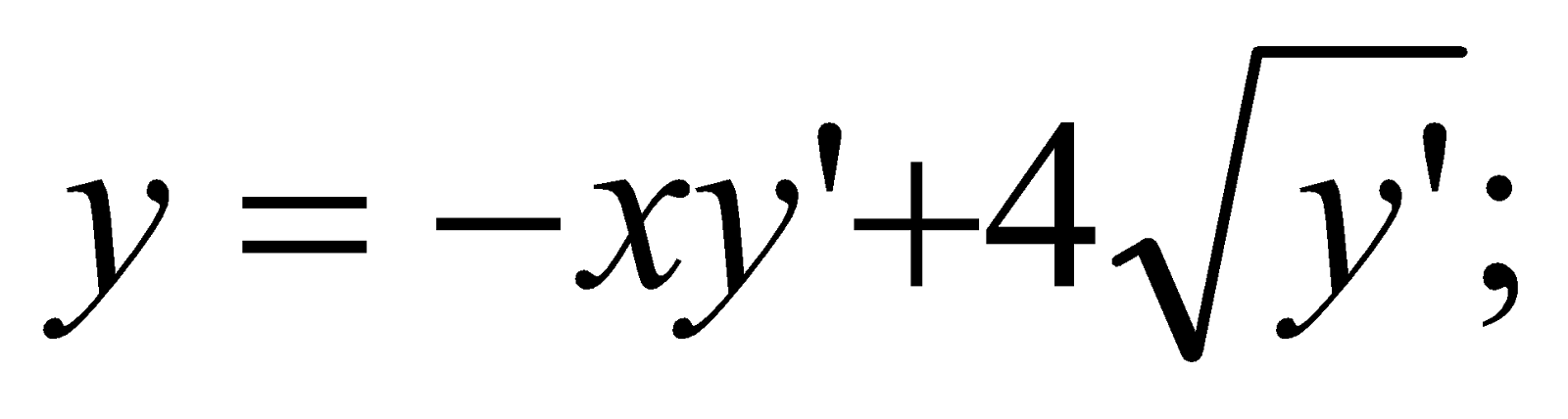
Розв’язати рівняння
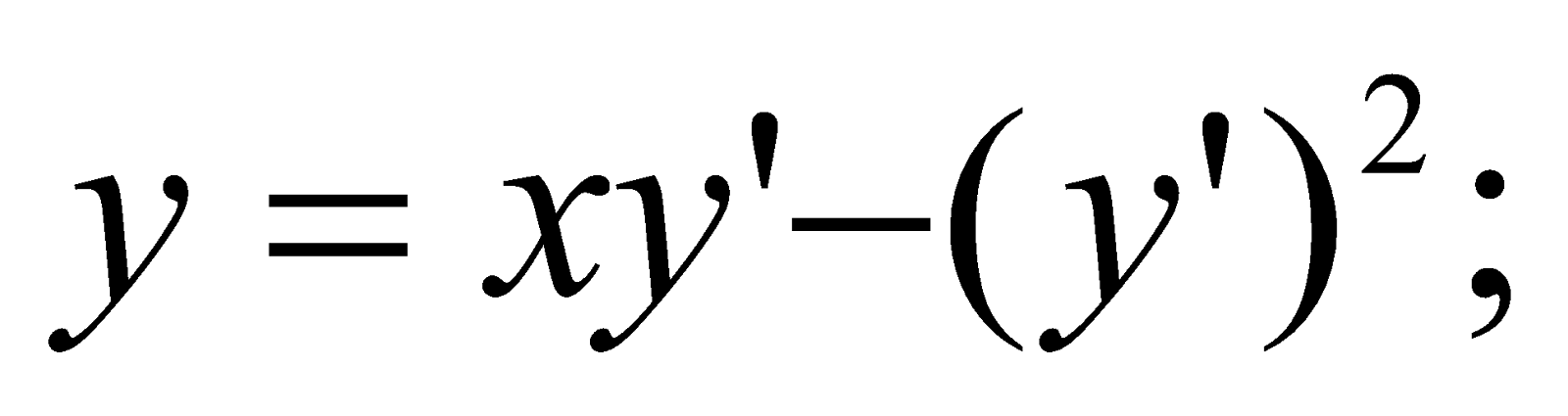
Розв’язати рівняння
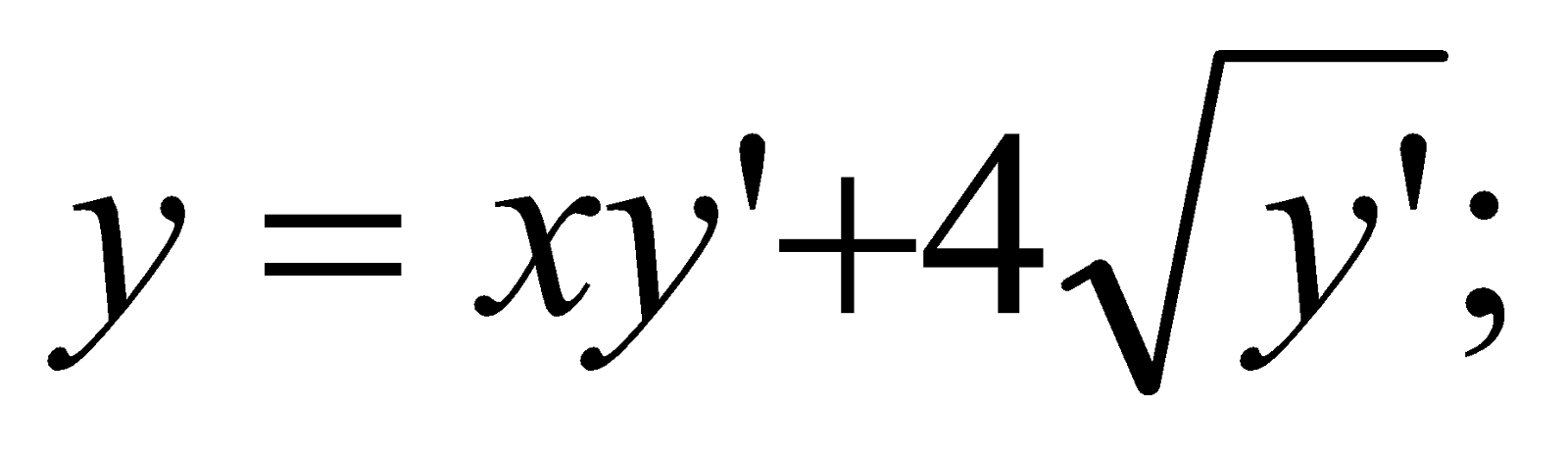
Розв’язати рівняння y-(y')2 =2(y')3
Розв’язати рівняння (y'')3+3y''-x=0
Знайти загальний розв’язок рівняння у(4)=cos2x
Розв’язати рівняння y''=x+sinx
Розв’язати рівняння y'''=x+cosx
Розв’язати рівняння (y'')3-2y''-x=0;
