І.Жансүгіров атындағы Жетісу мемлекеттік университеті	СМЖ ЖМУ Е/ОӘК.10-2012 3 басылым
	САПА МЕНЕДЖМЕНТ ЖҮЙЕСІ
	Дифференциалдық сынақ сұрақтары	Ф.4.10-121
		01.02.2009 ж

БЕКІТЕМІН

Математика және МОӘ кафедрасының

меңгерушісі_____ Кожашева Г.О

«___» ________________ 2014 ж.

Пән: Ықтималдық теориясы мен математикалық статистика

1. Жәшікте 4 ақ және 7 қара шар бар. Жәшіктен қалай болса солай бір шар алынған. Сол алынған шардың ақ болу ықтималдығы қалай?

2. Төрт ойын сүйегін лақтырғанда қанша жағдайлар болады. Төрт ойын сүйегі (e,i,j,k)

3. Терезеге 3 тас лақтырылды. Әрқайсысының дәл тию ықтималдығы бірдей және ол 1/3-ге тең. Терезеге дәл екі оқтың тию ықтималдығы неге тең.

4. Тәуелсіз 900 сынақтың әрқайсысына А оқиғасы р=0,8 ықтималдығымен орындалады. А оқиғасының:

5. 300 сынақ өткізілді. Сол сынақта А оқиғасы 240 рет пайда болады. Әр оқиғада пайда болған ықтималдықты табу керек. Әр оқиға р=0,75

6. Урнада a ак және b қара шар. Осы екеуін алған екеуінің түсі бірдей болу ықтималдығын тап

7. Үзіліссіз кезейсоқ шама үлестірім функциясымен берілген.

1. Үлестірім тығыздығын табу керек

2. M(x), D(x) табу керек

3. Мына интервалдан [1/2, 1] мән қабылдауының ықтималдығын табу керек

8. А оқиғасы тәжірибеде пайда болған ықтималдық 0,75-ке тең. Осы тәжірибеде оқиғанын пайда болған салыстырмалы жиілінігің оның ықтималдығының ауытқуының абсолют шамасы 0,05-тен артық болмауының ықтималдығы 0,96-ға тең болу үшін қанша тәжірибе жасау керек?

9. Бас орташа квадраттық ауытқуы σ=5 болатын қалыпты үлестіріммен берілген бас жинақтан алынған көлемі n=25 таңдамадан X_T=17 табылды. Бас жинақтың белгісіз математикалық үмітін γ=0,99 сенімділігімен бағалайтын интервалын тап.

10. Тәуелсіз 600 сынақтарда тұрақты р=0,8 ықтималдықпен пайда болған оқиғаның тура 228 рет пайда болу ықтималдығын табу керек

    

11. Дискретті кездейсоқ шама үлестірім қатарымен берілген

Х 2 4 5 6 8

Р 0,1 0,2 0,3 0,1 0,3

М(х), D(x), σ(x)- тарды табу керек?

12. Кездейсоқ шама дифференциялдық функциясы арқылы берілген

F(х)=

табу керек;

1. Коэффицент а-ны;

2. Үлестірім функциясын;

3. [0; ½] аралықтан мән қабылдау ықтималдығын.

13. Автобустың аялдамаға келу интервалы 10 мин. Кездейсоқ шама – автобусты күту уақыты. Осы кездейсоқ шаманың дифференциялдық және интегралдық функцияларын жазыңыз.

14. Кездейсоқ шама қалыпты үлестіріммен берілген: М(х)=30, D(х)=4.Мына теңсіздіктің /х-30/< ықтималдығы 0,8-ге тең болғанда қандай болу керек?

15. Кездейсоқ шама қалыпты үлестірім арқылы берілген. Математикалық үміті М(х)=5 дисперсиясы D(х)=0,64. Дифференциялдық функциясын жазыңыз. Мына [4; 7] интервалдан мән қабылдауының ықтималдығын табыңыз.

16. Үш бірдей жәшік бар. Бірінші жәшікте 26 ақ, екінші жәшікте 15 ақ және 11 қара, ал үшінші жәшікте 26 қара шар бар. Кездейсоқ жәшіктен ақ шар алынды. Байес формуласын пайдалана отырып ақ шар бірінші жәшіктен алынған ықтималдығын тап.

17. Студенттер сынақ сұрақтарының 75% ғана біледі. Оқытушы екі сұрақ таңдап студенттерге қояды. Студенттер осы сұрақтардың тым болмаса біреуіне жауап білетіндігінің ықтималдығын тап.

18. Қанша әдіспен 25 студентті 3 подгруппаға бөлуге болатын ықтималдықты тап.

19. Ойын сүйегі 6 рет лақтырылды. Сонын үшеуінде 6 санының түсу ықтималдығын тап.

20. Тиын 6 рет лақтырылды. Елтаңба екіден кем түспеу ықтималдығын тап.

21. Клиент магазинге келгенде сатылу ықтималдығы р=0,75 тең. 100 клиент болғанда сатылым жасау 80-ге тең болу ықтималдығын тап.

22. Дискретті кездейсоқ шама мына үлестіріммен берілсін

х -1 0 1 2

р 0,2 0,4 0,2 0,2

Сандық сипаттамаларын тап.

23. Айталық 11 бұйымның 8-і бірінші сортқа жатады. Кез – келген 5 бұйым алынды. Сонда осы 5 бұйымның ішінде бірінші сортты бұйымдардың болуының үлестірім кестесін құрыңыз.

24. Кездейсоқ шама дифференциалдық функциясы арқылы берілген

Интегралдық функцияны табыңыз. М(х), D(х)- тарды есептеңіз.

25. Кездейсоқ шама қалыпты үлестіріммен берілген: М(х)=30, D(х)=4.Мына теңсіздіктің /х-30/< ықтималдығы 0,8-ге тең болғанда қандай болу керек?

26. Зауытта дайындалған бұйымның 90 пайызы бірінші сортқа жатады. Тексеруге 600 бұйым алынды. Тексеруге алынған бұйымдардың ішіндегі бірінші сортқа жататын бұйымдардың үлесінің оның ықтималдығы 0,99-ға тең болуы үшін бұл ауытқу қандай болуы керек?

    

27. Бас жинақтан мынандай таңдама алынған

x_i 4 5 7

n_i 10 5 5

а) бас орташаның жылжымаған бағасын табу

б) бас дисперсиянын жылжымаған және жылжыған бағаларын табу.

28. Кездейсоқ шама қалыпты үлестірім арқылы берілген. Математикалық үміті М(х)=5 дисперсиясы D(х)=0,64. Дифференциялдық функциясын жазыңыз. Мына [4; 7] интервалдан мән қабылдауының ықтималдығын табыңыз.

29. Екі мерген атыс алаңында атыс жүргізуде. Бірінші мергеннің нысанаға тигізу ықтималдығы – 0,7, екіншісінікі – 0,8 тең. Егер екеуі де бір-бірден атыс жасаса, ең болмағанда біреуінің нысанаға дәл тигізетіндігінің ықтималдығы қандай?

30. Сүңгір қайықты іздеп табудың ықтималдығы 0,8, ал оны жойып жіберудің ықтималдығы 0,6 – ға тең. Іздеп табылған сүңгуір қайықты жойып жіберудің ықтималдығы қандай?

31. Қорапта бірдей бұйым бар. Қораптан екі сапалы бұйым алудың ықтималдығы 4/15 тең. Қорапта қанша сапалы бұйым бар еді?

32. Тұқымға арналған бидайдың дәндерінің ішінде 0,004% арам шөп дәндері кездеседі. Кез-келген 50000 дәндердің ішінде арамшөптің 5 дәндері кездесетіндігінің ықтималдығы қандай?

33. Ойнау шеберлігі тең екі шахматшы ойын көрсетуде.Үш ойында ең болмағанда бір ұтыс болуының ықтималдығын табу керек?

34. Дискретті кездейсоқ шама мына үлестіріммен берілсін

х -1 0 1 2

р 0,2 0,4 0,2 0,2

Сандық сипаттамаларын тап.

35. Кездейсоқ шама дифференциалдық функциясы арқылы берілген

Интегралдық функцияны табыңыз. М(х), D(х)- тарды есептеңіз.

36. Кездейсоқ шама интегралдық функциясы арқылы берілген

F(х)= Математикалық үмітті, дисперсияны табыңыз.

37. Зауыт өнімдерінің 75 процентін жоғарғы сортпен шығарады. Шығарылған 10000 бұйымдардың ішінде жоғарғы сортпен шығарылған бұйымдардың саны осы жоғарғы сортпен шығарылған бұйымдардың математикалық үмітінен айырмасының абсолют шамасы 1000 данадан артық болмауының ықтималдығын бағалаңыз.

    

38. Берілген вариациялық қатар арқылы X_T мен D_T тап.

X_i 3860 3900 3910 3913

N_i 2 13 4 1

39. Урнада 5 ақ және 50 ақ шарлар бар. Урнадан кез келген шар алынып түсі анықталғаннан кейін урнаға қайтарылады.Кездейсоқ шама Х-тәуелсіз 10 сынақта ақ шар пайда болуының саны. Осы кездейсоқ шаманың үлестірім заңын жазыңыз.

40. Урнада 5 ақ және 3 қара шар бар. Сол урнадан 2 шарды алғанда екеуі 2 түрлі түс болу ықтималдығын тап.

41. Топта 7 қыз және 3 ұл бала бар. Осы топтағы студенттер арасында 4 билет ойнатылып жатыр. Осы билетті 2 қыз бала және 2 ұл бала алатын ықтималдығын тап.

42. Ұл баланың туылу ықтималдығы 0,5 тең. 200 баланың ішінде 90 ұл бала болу ықтималдығын тап.

43. Екі кездейсоқ Х және Ү шамалар системасы үлестірім функциясымен берілген.

F(x)={

Үлестірім тығыздықтарын f(x,y), f₁(x), f₂(y) және f₁(x), f₂(y)-тап.

44. Тәуелсіз 900 сынақтың әрқайсысына А оқиғасы р=0.8 ықтималдығымен орындалады. А оқиғасын 750 рет орындалу ықтималдығын тап.

45. Белгілі бір шаманың мәні ретінде мейлінше көп өлшемдердің арифметикалық орташа нәтижесі алынады. Әрбір өлшеудің мүмкін мәндері орташа квадраттық ауытқуы 1 сантиметрден аспайды деп қарастырып 1000 өлшеуде алынған нәтиженің берілген шаманың шын мәнінен ауытқуының 0,1 сантиметрден артық болмауының ықтималдығын тап.

46. Кездейсоқ шама үлестірім тығыздығымен берілсін

F(x)={

47. Екі тәуелсіз кездейсоқ шамалар Х және У үлестірім кестелерімен берілген

х 0 3 4 у 2 3

p 0,2 0,6 0,2 p 0,3 0,7

х+у, х -кездейсоқ шамалардың иатематикалық үміттері мен дисперсияларын тап.

48. Айталық дайындалған бөлшектің бір өлшемі қалыпты үлестіріммен берілген кездейсоқ шама болсын, математикалық үміті а=10см, ал 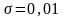. 1) Кездейсоқ шаманың өзінің математикалық үмітінен ауытқуы 0,025 артпауының ықтималдығын табыңыз; 2) Бөлшектің өлшемі 10,03 сантиметрден артпайтындығының ықтималдығын табыңыз; 3) Кездейсоқ шаманың өзінің математикалық үмітінен ауытқуы +0,02-ге тең болуының ықтималдығы 0,99 болуы үшін бөлшектің дайындалуының дәлдігін сипаттайтын қандай болуы керек?

49. Z=x+2y-2 D(x)=2, D(y)=1, D(z)=?

50. Z=ax+by+c D(x)=2, D(y)=1, D(z)=?

51. Дискреттік кездейсоқ Х шамасы орналастыру заңы бойынша төмендегідей берілген:

Х	1	3
Р	0,4	0,6

Алғашқы бірінші, екінші және үшінші ретін табыныз?

52. Оқулық 100 000 таралымда басылып шығарылды. Оқулықтың дұрыс емес жинақталу ықтималдығы 0,0001 – ге тең. Осы таралым арасында 5 кітаптың ақау кеткендігінің ықтималдығын табу керек?

53. Кітапхана сөресінде 15 оқулық қатарымен тізіліп тұр, оның бесеуі түптеу қабымен. Кітапханашы кез-келген 3 оқулықты алады.Осы оқулықтардың ең болмаса біреуі түптеу қабында болатындығының ықтималдығын табыңыз?

54. Кездейсоқ шама дифференциалдық формуласы арқылы берілген:

Табу керек: