2.2. Өзқауымдық дәрежесінің сандық белгі-шарттары

Реалды объектілер, оның ішінде Күн, сыртқы әлеммен зат және энергиямен алмасатын бейсызық ашық жүйенің мысалы болып табылады. Күннің радиосәулеленуі кезінде симметрияның бұзылуы, құрылымдық пен ықтималдылық сипаты байқалады. Табиғи құрылымдалу кезінде хаостан реттілік, яғни өзқауымдық пайда болуы мүмкін. Бұл мәселелерді негізгі екі түсінік: информация және энтропия арқылы түсіндіруге болады. Қазіргі кезде бұл мәселені шешудің жалғыз жолы – энтропиялық әдіс, себебі, энтропия хаос пен күрделіліктің жалғыз белгілі өлшемі болып табылады. Энтропияның эволюциясы бойынша ғылымда бірнеше нәтижелер белгілі: Больцман, И. Пригожин, Ю. Климонтович теоремалары. Әуелі Больцманның Н-теоремасы тұжырымдалды, ол тұйық жүйеде энтропияның өсуі туралы болды. Ғылым дамуымен Пригожин теоремасында өзқауымдық белгісі анықталды, ол бойынша өзқауым процестерде энтропия өндірісі минималды, ал содан кейін Климонтовичтің S-теоремасында энтропия өзқауым кезінде кемитіні дәлелденді. Бірақ, бұл аталған теоремаларда күрделі жүйелердің өзқауым дәрежесінің сандық белгі-шарттары анықталмады. Бұл сандық информациялы-энтропиялық белгі-шарттар алғаш рет 1996 жылы Қазақстандық профессор (әл-Фараби атындағы ҚазҰУ) З.Ж. Жаңабаевтың жұмыстарында алынды. Бұл нәтижелер төменде келтірілген.

Жалпы қабылданған терминологияға сәйкес I_i информациясы, P_i ықтималдыққа ие құрылым пайда болғанда (жоғалғанда) (2) формуламен есептелінеді және келесі түрде табылады:

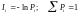, (16)

ал оның орта мәні – информациялық энтропия (8)-өрнекпен анықталады.

Әртүрлі иерархиялық деңгейлердегі өзұқсастық, өзқауымдық жүйелердің әмбебаптық қасиеттерінің бірі болып табылады. Олардың сипаттамасының масштабты инварианттылығы информацияның үздіксіз мәндерін қабылдауға мүмкіндік береді. Ал информацияны анықтаушы физикалық шама ретінде қабылдауға болады. Мұндай жағдайлар, алдымен күй функцияларының арасында (мысалы энергия мен энтропияның арасында) бірмәнді емес байланыс орнайтын күшті бейсызық динамикалы-информациялық жүйелерге (турбулентті орта, биологиялық объектілер т.б.) қатысты.

Сондықтан, информацияның байқалу ықтималдылығы жөнінде айтуға болады:

. (17)

P(I) ықтималдықты f(I) ықтималдықтың таралу тығыздығының функциясы арқылы жазсақ:

, (18)

мұндағы интеграл шектері аймаққа сәйкес келеді. Демек, 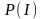– информацияның байқалу ықтималдық функциясы – ықтималдықтың таралу тығыздығының функциясымен сәйкес келеді. Информация күрделі жүйелердің барлық иерархиялық деңгейлерінің жалпы және толық сипаттамасы болып табылады: жүйенің бір бөлігі жалпы жүйе туралы мәліметті қамтиды.

(18) формуланы ескере отырып, өзұқсас жүйелердің информациялық энтропиясын келесі түрде жазамыз:

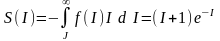. (19)

үшін 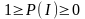және 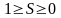болады.

Өзқауымдық жүйенің өзұқсастығы қандай да бір сипаттамалы 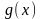функциясының мына функционалды теңдеуге сәйкестігімен сипатталады:

, (20)

мұндағы  – масштабты көбейткіш. Кез-келген үздіксіз функция өзінің қозғалмайтын нүктесінде (20) теңдеуді қанағаттандырады. Сипаттамалық функция ретінде f(I) – ықтималдық тығыздығын және – информациялық энтропияны қабылдап, олардың қозғалмайтын нүктелерін табайық:

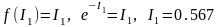, (21)

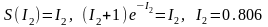. (22)

Бұл қозғалмайтын нүктелер бірмәнді орнықты, себебі олар, сонымен қатар, информацияның кез-келген бастапқы мәніне сай шексіз бейнелеудің шегі болып табылады:

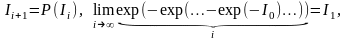(23)

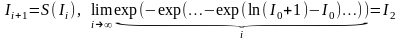. (24)

сандарының мағынасын әртүрлі түсіндіруге болады. Олардың ішіндегі ең әмбебабы – Фибоначчи санын (жүйенің динамикалық өлшемі – «алтын қима») қолдану аймағының кеңейуі. саны информациялық (локальді) сипаттауына, ал 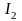саны күрделі жүйені энтропиялық (орталанған) сипаттауға сәйкес келеді. болса (22)-ден (21) шығады, бойынша экспонентаны жіктеудің бірінші мүшесін ескерсек, онда (22)-ден 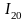– Фибоначчи саны үшін теңдеу аламыз:

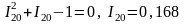, (25)

(21) теңдеуден I – I₁₀ = I₁₀, I₁₀ = 0,5.

Сонымен, тәжірибеде күрделі жүйенің өзқауым күйі S[I₂₀  I₂] жағдайда, қарапайым жүйенің өзұқсас жағдай I[I₁₀, I₁] болғанда байқалуы тиіс.

Төменде (21), (22) тәуелділіктерді тұрғызуға арналған бағдарлама және сплайн интерполяцияның көмегімен тұрғызылған график келтірілген (3-сурет).

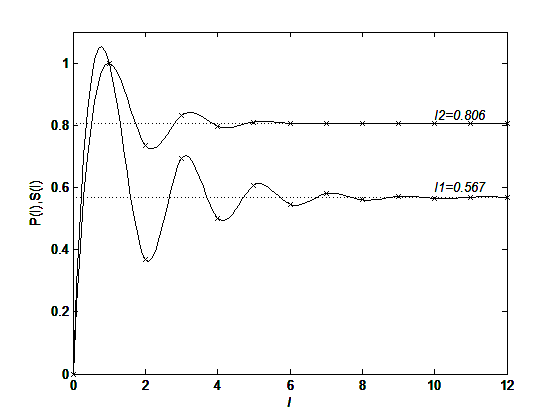
Сурет 6. Информация және энтропияның сипаттық уақыт бойынша өзгерісі

I₁, I₂ сандарының мағынасын жалпылама пайымдаулармен толығырақ ашуға болады. Шеннон бойынша Y берілген кездегі Х шамасы туралы информация шартсыз және шартты энтропиялардың айырымы ретінде анықталады:

S(X) – S(X/Y) = I(X)  0. (26)

S(X) шамасын «Физикалық хаостың» энтропиясының анықталмағандығының нормасы ретінде қабылдап, (26)-ны мына түрде жазамыз:

I + S = 1, (27)

мұндағы I – анықталғандықтың салыстырмалы өлшемі (информация), S – қандайда бір Х сипаттасы бойынша жүйе туралы анықталмағандықтың салыстырмалы өлшемі (энтропиясы). Жалпы мағынада (27) өрнек кез-келген табиғаттың күрделі жүйелерін өзара байланысқан альтернативті сипаттамаларын байланыстырады: тәртіп және хаос, симметрия және асимметрия, рационалды және иррационалды, детерминизм және индетерминизм және т.б. Альтернативті сипаттамалардың үйлесімі олардың салыстырмалы өлшемінің өзгеруінің пропорционалдылығын болжайды:

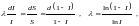(28)

мұнда I, S өлшем бірліктерін таңдау еркіндігі мүмкін болғандықтан интегралдау тұрақтысы нөлге тең деп алынған. Дербес жағдайда  параметріне және I айнымалысына айқын мағына беретін

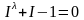(29)

алгебралық теңдеуі (28) формулаға эквивалентті. М. Фейгенбаум орнатқан табиғи құбылыстардың әмбебап даму заңдылығының периодты екі еселенуінің бифуркациясын негізге алайық. Жүйенің даму деңгейінің иерархиялық күрделілігін ретіне n-ге сәйкестендіріп,  = 2ⁿ деп қарастырайық. n = 0,  = 1 жүйенің статикалық күйіне сәйкес келеді және (29)-дан I = S екені шығады. Динамикалық жүйенің бірінші иерархиялық даму деңгейі (n = 1,  = 2) Фибоначчи (I₃ = 0.618) санына тең сипаттамалардың пропорциясымен анықталады. Статикалық және динамикалық күйлердің (құрылымның және стохастиканың бастауы) арасында I₁ саны арқылы сипатталатын жүйенің информациялық күйі жүзеге асады.  =1.5 деп алып, (29)-дан I = 0.57  I₁ болатындығын көреміз. Ли–Йорктің «үш период хаосты білдіреді» атты теоремасы бойынша n = 3 жағдай ішкі тәртібі бар ең күрделі статистикалық күйді I₂ энтропия функциясының қозғалмайтын нүктесімен сипаттайды.  = 2³ = 8 үшін (29)-теңдеудің шешімі I = 0.811  I₂ болып табылады.