«Попади в обезьяну» движение в среде с сопротивлением

(Иллюстративный пример)

Иллюстративный пример.

Пункт А находится на бетонированном аэродроме, пункт В — на примыкающем к нему поле, на котором скорость машины в п раз меньше. Для того, чтобы за кратчайшее время добраться из А в В, был выбран оптимальный маршрут, показанный на рисунке. Найти соотношение между синусами углов α и β.

Рис. :

Оптимальный маршрут из пункта А в пункт В (к иллюстративному примеру.)

Полное время в пути: τ =

Потребуем, чтобы полное время было минимальным: τ= Δ + Δ , где

Δ

;

Δ –

=

Таким образом, полное время в пути

τ= Δ + Δ =

Поскольку точка О была выбрана так, чтобы на путь затрачивалось минимальное время, поэтому должна быть равна нулю производная времени τ по расстоянию х:

= = 0

Поскольку

,

находим

sin α - nsinβ = 0, т.е.

= n

Мы получили выражение, сходное с известным законом преломления света на границе двух сред, разной оптической плотности. Это сходство не случайно: природа устроена так, что свет распространяется по такому пути, для прохождения которого требуется минимальное время. (т.е. свет выбирает оптимальный путь)

Принцип ФЕРМА.

ЗАКОНЫ СОХРАНЕНИЯ ЭНЕРГИИ И ИМПУЛЬСА

Однородность времени (закон сохранения энергии)

Однородность и изотропия пространства (закон сохранения импульса и закон сохранения момента импульса)

Основы динамики

Иллюстративный пример

Абсолютно упругое тело падает в воздухе с достаточно большой высоты (!)

v → = С каким ускорением будет двигаться тело после абсолютно упругого соударения с плоской поверхностью.

«До»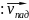 = = - m

«После»: ( = =

m = + m = 0 = - m

После отражения:

m = = + m = 2m ( )

= 2 (!)

«Я из книг по физике

Почерпнул больше математики,

Чем из математических книг.»

Энрико Ферми.

Л Е К Ц И Я №3

ЗАКОНЫ СОХРАНЕНИЯ ЭНЕРГИИ И ИМПУЛЬСА

Однородность времени (закон сохранения энергии)

Однородность и изотропия пространства (закон сохранения импульса и закон сохранения момента импульса)

Основы динамики

Иллюстративный пример

Вертолет массой m=3т висит в воздухе. Определить мощность N, развиваемую мотором вертолета, если диаметр винта равен d = 8м. (При расчете принять, что винт отбрасывает вниз цилиндрическую струю воздуха диаметром, равным диаметру винта. Плотность воздуха принять, равной ρ = 1,29 )

Решение:

Сначала используем метод анализа размерностей. Искомая мощность зависит от:

1. массы (веса) вертолета (mg);

2. диаметра винта (d) и;

3. плотности воздуха (ρ).

Искомое соотношение для мощности должно иметь вид:

N = Const (mg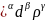

Таким образом:

M 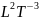= (ML (M =

Решая систему уравнений:

получаем: α = 3/2; γ = - 1/2; β = -1.

Следовательно,

N = Const =

Д.З.

Решить эту задачу точно (самостоятельно) (См. с 64. Т.1)

Решение:

Пусть скорость струи воздуха, отбрасываемого винтом v. За время Δt частицы воздуха проходят расстояние Δh = v Δt.

Таким образом, за время Δt винт вертолета придает скорость v всем

частицам воздуха, находящимся в цилиндре с площадью основания

и высотой Δh. Масса воздуха Δm в этом объеме равна:

Δm = ρ v Δt (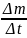 = ρ v )

и его кинетическая энергия ΔТ определяется выражением:

ΔТ = = Δt ρ .

Мотор передает воздуху кинетическую энергию ΔТ, т.е. совершает работу

ΔA = ΔT = Δt ρ .

Следовательно, развиваемая мотором мощность

N = = ρ

В этом соотношении следует определить скорость v струи воздуха, отбрасываемого винтом. Импульс Δp, передаваемый частицам воздуха за время Δt:

Δp = Δm v = ρ Δt .

Из второго закона Ньютона ( = F) – сила, действующая на вертолет со стороны отбрасываемого воздуха должна быть равна весу вертолета:

F = mg = ρ ( = v = v ρ v

Таким образом, v = . Следовательно,

N = = ρ = ρ ( =