
- •Структура курса
- •Проблемы:
- •Анализ теории размерностей
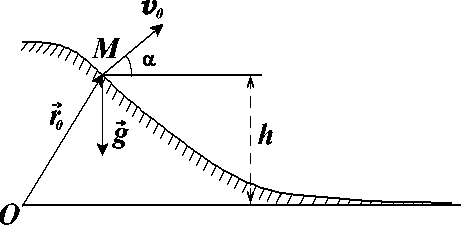
- •Дальность полета.
- •Максимальная дальность полета (при h ≠ 0).
- •«Попади в обезьяну» движение в среде с сопротивлением
- •Основы динамики
- •Основы динамики
- •Законы сохранения
- •Уравнение и.В. Мещерского (1859 – 1935)
- •Законы кеплера
- •Гравитационный потенциал.
- •Принцип эквивалентности масс
- •Космические скорости
- •Неинерциальные системы отсчета:
- •Центробежная сила инерции:
«Физика – прежде всего живое творение рук и мозга,
которое передается более примером, чем зубрежкой.
Она (физика) воплощает искусство решать проблемы
материального мира. И поэтому физике надо учиться,
но учиться как искусству.»
А.Б. Пиппард.
«При изучении наук (физики) примеры полезнее правил.»
Исаак Ньютон.
Л Е К Ц И Я 1
Структура курса
Лекции + Семинары → Зачет + Экзамен
Экзамен: Письменно – Устный
Ведение конспекта и (+) работа с конспектом
Приглашение в «лаборанты»
Проблемы:
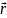 (t)
=
(t)
=
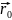 +
+
 t +
t +

(t)
=
+

Если a = const, что будет при t →∞ (v>c ?)
 =
?
=
?
(t)
=

g = 9.8
 P
= mg
P
= mg
Северный полюс (широта 90ᵒ) = 9.83245
Исландия = 9.8253
С.-Петербург = 9.8193
Москва = 9.8094
Сингапур = 9.7816
Экватор (широта 0ᵒ) = 9.7803
1 + 1 = 0
1 + 1 = 2
1 + 1 = 4
Точка движется по кривой в одну сторону. Определить с помощью предложенного графика момент времени t*, в который мгновенная скорость равна средней скорости за первые t* секунд движения.
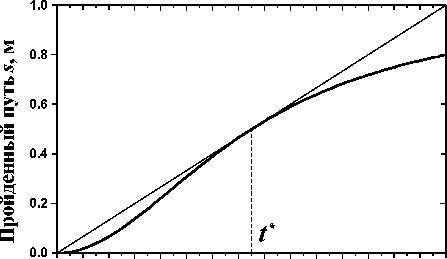
О 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Время t, с
Рис.: В точке t* = 7.5 с мгновенное значение скорости v совпадает со средней скоростью vcp за период времени от t = 0 до t = t*
Задача П.Л. Капицы о возвращении космонавта на космический корабль.
Анализ теории размерностей
Любой физический закон и описывающее его уравнение не зависят от выбранной нами системы единиц.
Закон природы описывает соотношение между величинами, которое существовало до нас, существует независимо от нас и будет существовать после нас. А система единиц – дело произвольного соглашения между людьми.
Обе части любого равенства должны иметь одинаковые размерности.
СИ – Syste'me International
м (метр) - length (L)
с (секунда) - time (T)
кг (килограмм) - mass (M)
А (ампер) - сила тока
К (кельвин) - температура
кд (кандела) - сила света
моль (моль) - количество вещества
Время – свойство материальных процессов иметь определенную длительность, следовать друг за другом в определенной последовательности и развиваться по этапам и стадиям.
Д.З.:
Площадь
–

Объем
–

Скорость
– L
Ускорение
– L
Плотность
– M
Импульс – ML
Сила – ML
Энергия
– M
Частота –
Момента
импульса – M
Давление
– M
и т.д.
МЕТР
Рассматривается
переход электрона в атоме криптона
 между квантовыми состояниями 2
между квантовыми состояниями 2 и 5
и 5 .
Метр содержит 1650763,73 длины волны в
вакууме этой спектральной линии.
.
Метр содержит 1650763,73 длины волны в
вакууме этой спектральной линии.
СЕКУНДА
Раньше:
Секунда
-
 средних солнечных суток. (1 сутки = 24
часа =1440 минут = 86400 секунд)
средних солнечных суток. (1 сутки = 24
часа =1440 минут = 86400 секунд)
Секунда
– продолжительность 9192631770 периодов
излучения, соответствующего переходу
между сверхтонкими уровнями основного
состояния атома цезия
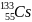
c
= 2.99792458·
1 нановек = π секунд
Иллюстративный пример:
На тело массой М действует постоянная сила F на пути s. Определить скорость, которую приобретет тело в конце пути.
v
= Const

L
=
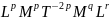
p =1/2; q = -1/2; r =1/2.
v
= Const
 =
=
v
=
 ; v
=
;
; v
=
;
 (Замечания
о числе РЕЙНОЛЬДСА)
(Замечания
о числе РЕЙНОЛЬДСА)
 установившейся
скоростью будет двигаться парашютист,
совершающий затяжной прыжок?
установившейся
скоростью будет двигаться парашютист,
совершающий затяжной прыжок?
 =
mg -
=
mg -
 v
→
→
v
→
→ =
0
=
0
Следовательно: = mg
=Const

 =
ML
=
ML
ML
= (

Таким образом,
p = 1; q = 1; r =2,
т.е.
F
= Const Sρ C= ½.
C= ½.
=mg
→ Sρ
=mg
Sρ
=mg
=

 .
.
установившейся скоростью будет двигаться парашютист, совершающий затяжной прыжок?
Было показано, что = Sρ
Уравнение движения имеет вид:
= mg - С , где С = Sρ
=
g
-
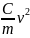 (Начальные
условия: t
=
(Начальные
условия: t
=
 =0 →
=0 →
 = v(
=0) = 0!)
= v(
=0) = 0!)
Разделяем переменные:
 =
dt
=
dt
 =
=
 =
=

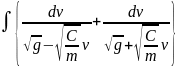 =
=

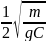
 =
t + Const
=
t + Const
С учетом начальных условий: =0; = 0, получаем
v(t)
=

v(t)
=

При
t
»
 v
→
v
→
 =
=
Зависимость силы сопротивления среды от скорости движущегося объекта.
Число РЕЙНОЛЬДСА
Re
=
 ρv,
ρv,
где ρ – плотность среды; η – коэффициент вязкости среды
 =
1.29
=
1.29

 =
1708·
=
1708·
 (
= 1,8·
(
= 1,8·

При
малых скоростях Re
< 1
= Const
η
Const
η v
v
При больших скоростях Re > 1 = Sρ
Оценка
критической скорости для движения
объекта (для определенности S
= 1
 в воздухе:
в воздухе:
 ~
~
 = 1.3·
м/с.
= 1.3·
м/с.
Д.З. Проблема:
Тело
массой m
колеблется на конце пружины с амплитудой
А (т.е. 4А – это расстояние, проходимое
телом за период колебаний). Используя
анализ размерностей, определить
зависимость периода колебаний от
величин m,
A
и коэффициента жесткости пружины k
(Закон Гука:
 = - kx)
= - kx)
T
~

 =
=
 = M
= M
 =
=


s = -1/2; q = ½; p = 0
Таким
образом, T
~

Д.З. Проблема:
Определить
зависимость продолжительности жизни
(Т) от размеров мозга (L),
массы тела (М), скорости обмена веществ
( )
(в калориях в секунду).
)
(в калориях в секунду).
T
= Const

Размерность
(
):
 =
=
 =
=
T
=
 =
=

s = -1/3; p =+2/3; q = +1/3
Итак,
Т
= Const
Л Е К Ц И Я 2

Принцип независимости движений. (Принцип суперпозиции (наложения))
 =
=
 =
=
=
+
t
+

=
+
 t
t
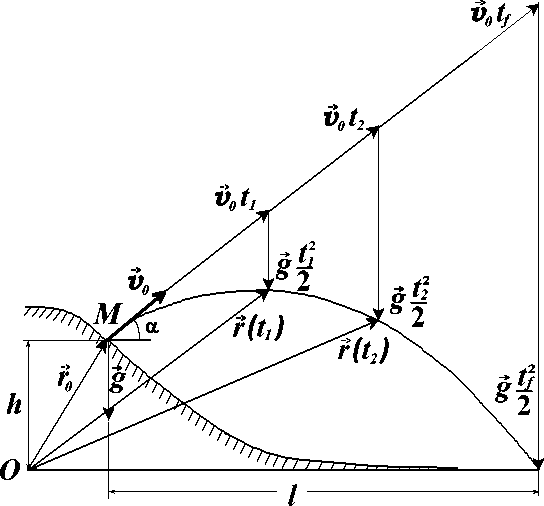
ПРИНЦИП НЕЗАВИСИМОСТИ ДВИЖЕНИЙ
x(t) = t
y(t)
= h +
t
sinα -

Исключаем время t и получаем траекторию
y(x)
= h + tg α·x -

y(x)
= h
+ A·x
- B· (уравнение параболы, где A=tgα;
B=
(уравнение параболы, где A=tgα;
B=
