Лист 3.

1. Проиллюстрируйте применение основной теоремы зацепления на примере спроектированной эвольвентной зубчатой передачи (покажите сопряженные профили, контактную точку и ее геометрическое место в процессе взаимодействия профилей, полюс зацепления, отрезки, отношение которых определяет передаточное отношение передачи).

Ответ: поверхности элементов высшей кинематической пары, обеспечивающие заданный закон движения, называют сопряженными поверхностями. Геометрическое место контактной точки – отрезок В1В2 – практическая линия зацепления. Отрезки – расстояния от осей колес до полюса зацепления.

2. Назовите параметры исходного производящего контура. Какие поверхности называют сопряженными и производящими поверхностями?

Ответ: производящей поверхностью называется поверхность, которая в процессе технологического движения позволяет получить необходимую сопряженную с ней поверхность. ИПК – след режущих кромок инструмента во время рабочего хода на плоскости, перпендикулярной оси колеса. Параметры ИПК:

1. Модуль m;

2. Угол главного профиля «альфа»;

3. Коэффициент высоты головки h*a;

4. Коэффициент радиального зазора c*.

3. Что называют зубчатым и станочным зацеплением? Какие линии являются начальными в зубчатом и станочном зацеплениях? Покажите их на чертеже.

Ответ: Станочное зацепление – зацепление заготовки и инструмента. Зубчатое зацепление – кинематическая пара, образованная зубчатыми колесами передачи. В зубчатом зацеплении начальными линиями являются окружности, а в станочном – окружность и прямая (и в том, и в другом случае они катятся друг по другу без проскальзывания).

4. Рассмотрите основные свойства эвольвентного профиля на примере спроектированного зубчатого колеса.

Ответ:

1. Показать, что линия зацепления – прямая, не меняющая своего положения в пространстве. Следовательно, передаточное отношение остается постоянным.

2. Показать, что поверхностью, сопряженной с поверхностью зуба колеса, является прямая (при бесконечном радиусе основной окружности эвольвента переходит в прямую).

3. Общей нормалью является прямая, касательная к основной окружности (показать линию зацепления).

4. Радиус кривизны равен отрезку от эвольвенты до основной окружности (показать эти отрезки).

5. Перечислите основные свойства эвольвентного зацепления и проиллюстрируйте из применение в спроектированном механизме.

Ответ: см. предыдущий вопрос.

6. Как влияет относительное положение исходного производящего контура на размеры проектируемого колеса и качественные зубчатой передачи.

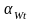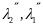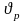Ответ: - коэффициент торцевого перекрытия. Определяет плавность и бесшумность работы передачи. - угол зацепления передачи. - коэффициенты скольжения. Определяют интенсивность износа. - коэффициент удельного давления. Определяет интенсивность усталостного выкрашивания (особенно важен для передач, работающих в смазке). - толщина зубьев по дугам окружностей вершин. Они (а вернее, их отношения к модулю передачи) не должны быть меньше определенного значения (иначе – заострение зуба). Их динамику смотри по полученным графиками.

7. Какие технологические методы используют для образования боковых поверхностей цилиндрических зубчатых колес?

Ответ: огибание, нарезание.

8. Отличаются ли угол зацепления и угол станочного зацепления? При каких условиях они равны.

Ответ: да, в общем случае отличаются. Для положительной передачи больше угол зацепления, а для отрицательной – угол станочного зацепления. Равны они только для передачи без смещения.

9. Покажите углы профиля в точках эвольвенты на делительно окружности и на окружности вершин.

Ответ: для этого проводим касательную к профилю и измеряем угол с радиальным направлением.

10. Покажите основные параметры зубчатого зацепления и расскажите, от каких факторов они зависят.

Ответ: Основные параметры зубчатых колес:

1. Диаметр делительно окружности d;

2. Окружной шаг зубьев по делительной окружности;

3. Модуль;

4. Высота делительной головки зуба ha – расстояние между делительной окружностью колеса и окружностью вершин;

5. Высота делительной ножки зуба hf – расстояние между делительной окружностью колеса и окружностью впадин;

6. Диаметр окружность вершин da;

7. Диаметр окружности впадин df.

8. Остальное – по вкусу.

11. Расскажите о подрезании зубьев. Как обеспечивается в станочном зацеплении образование зуба без подрезания? Покажите на чертеже отрезки, пропорциональные смещениям исходного контура относительно заготовки в радиальном направлении и в направлении движения контактной точки профилей.

Ответ: подрезание зуба – уменьшение эвольвентной части зуба и ослабление его в опасном сечении. Начало подрезание – равенство теоретической и практической линии зацепления. Смещение в радиально направлении – это x1m. Для обеспечения без подрезания делают зубчатые колеса с числом зубьев больше минимально допустимого (17).

12. Расскажите о линии зацепления в эвольвентном и станочном зацеплении. От каких величин зависит длина активной линии зацепления?

Ответ: от углов профилей по вершинам окружностей и угла зацепления.

g_a = r_b2 (tga_a2 - tga_tW) + r_b1 (tga_a1 - tga_tW)

эту зависимость можно также выразить через коэффициенты смещения, угол зацепления и радиусы начальных окружностей.

13. Что характеризует коэффициент торцевого перекрытия? Покажите отрезки на чертеже, отношение которых равно коэффициенту перекрытия в эвольвентном зацеплении. Сопоставьте отношение этих отрезков с расчетным значением.

Ответ: отношения двух отрезков я не нашел, но коэффициент перекрытия равен отношению длины активной линии зацепления к шагу по основной окружности (неважно, чего).

14. Что характеризует коэффициент удельного скольжения профилей в зубчатом зацеплении? Покажите, от каких параметров на чертеже зависит скорость скольжения в контактной точке профилей. Как определить коэффициент скольжения в граничных точках активной линии зацепления?

Ответ: коэффициент удельного скольжения характеризует скорость скольжения профилей в зубчатом зацеплении и, как следствие, интенсивность изнашивания и отслаивания материала с поверхностей зубьев.

- формулы для определения коэффициентов скольжения в граничных точках.

15. Что характеризует коэффициент удельного давления в зубчатом зацеплении? Как он определяется? Покажите отрезки на чертеже, характеризующие кривизну профилей в контактной точке.

Ответ: коэффициент удельного давления учитывает влияние геометрии зубьев (радиусов кривизны их профилей) на величину контактных напряжений, возникающих в местах соприкосновения зубьев. Коэффициент удельного давления определяется как отношение модуля зацепления к приведенному радиусу кривизны. Для определения радиусов кривизны проводим касательные к основным окружностям (для точки зацепления – части теоретической линии зацепления).

16. Поясните, как выбраны коэффициенты смещения исходного производящего контура при расчет зубчатой передачи? Имеется ли запас смещения по условиям ограничения от подрезания и как его можно оценить по изображенной схеме станочного зацепления?

Ответ: в данной работе выбирался только коэффициент ИПК для шестерни по условию отсутствия подрезания (минимальный коэффициент смещения) и заострения (максимальный коэффициент смещения) зубьев. Запас имеется, так как точки Bl иNl не совпадают. Оценить запас можно по расстоянию между ними (небольшое).

17. Расскажите о последовательности графических построений при синтезе сопряженных профилей в станочном зацеплении. Какие траектории описывают отдельные точки исходного производящего контура при движении огибания? Как получена сопряженная поверхность зубчатого колеса?

Ответ: см. методу, там этот вопрос подробно расписан.

18. Назовите особенности сложных зубчатых механизмов, зубчатых планетарных редукторов и дифференциалов (имеются в виду структурные особенности?). Как описать структурную формулу для определения числа степеней свободы зубчатого механизма? Используйте эту формулу для анализа спроектированных зубчатых передач и планетарного механизма.

Ответ: в плоских механизмах свободными остаются два движения зубчатых колес относительно друг друга – скольжение одного колеса по поверхности зуба другого колеса и перекатывание без скольжения, поэтому в этих механизмах зубчатое зацепление – это кинематическая пара 4 класса. Зубчатые колеса со стойками образуют вращательные кинематические пары. Степень подвижности таких механизмов можно определять по формуле Чебышева: W=3n-2p₅-p₄.

Планетарный механизм – это механизм, в состав которого входят звенья с подвижной осью вращения.

Дифференциальный планетарный механизм – это планетарный механизм со степенью подвижности не менее 2.

19. Используя графические построения распределения линейных скоростей звеньев планетарного редуктора, покажите направление угловых скоростей звеньев в относительном движении на примере следующих кинематических пар: водило – стойка, центральное входное колесо – стойка, водило – блок сателлитов, сателлит – опорное зубчатое колесо. Какое звено имеет наибольшую угловую скорость в абсолютном и относительном движениях?

Ответ: Все распределения – смотри чертеж. Угловая скорость пропорциональна тангенсу угла наклона. Переносным движением сателлита является вращение водила, относительным – вращение вокруг своей оси. В абсолютном движении угловая скорость пропорциональна тангенсу угла наклона ЛРС сателлита. В относительном движении ищем разность тангенсов.

20. Покажите на схеме планетарного редуктора оси мгновенного вращения звеньев в относительном движении. Как вы их использовали при кинематическом анализе планетарного механизма?

Ответ: оси мгновенного вращения в относительном движении – это точки контакта начальных окружностей соответствующих зубчатых колес. При переходе к абсолютном движению скорости точек различных звеньев на осях равны.

21. Пользуясь схемой рабочего и станочного зацеплений, определите коэффициенты перекрытия через отношения соответствующих отрезков. Какая их этих величин больше и почему?

Ответ: больше будет коэффициент перекрытия со станочных зацеплением, так как у него длиннее активная часть линии зацепления (почему).

22.На схеме рабочего зацепления колес покажите углы профиля на окружностях вершин и их инволюты.

Ответ: про угол я уже говорил, а инволютой эвольвенты является основная окружность.

23. На профиле зуба шестерни обозначьте произвольную точку и графическим методом найдите сопряженную точку на профиле зуба колеса. Укажите место контакта этих двух точек на линии зацепления.

Ответ: произвольную точку катим до линии зацепления, находим точку контакта и катим ее до пересечения с зубом колеса.

24. Сопоставьте выбранное смещение с минимальным смещение и покажите на схеме станочного зацепления отрезок, пропорциональный этой разности.

Ответ:

25. Расскажите о назначении уравнительного смещения.

Ответ: Уравнительное смещение D y*m - условная расчетная величина, введенная в расчет геометрии зацепления с целью обеспечения стандартного радиального зазора в зацеплении (величина, выражающая в долях модуля уменьшение радиуса окружностей вершин колес, необходимое для обеспечения стандартной величины радиального зазора).

26. На линии зацепления покажите точки пересопряжения профилей зубьев. Как они расположены относительно граничных точек В1 и В2 рабочего участка линии зацепления?

Ответ: следующий зуб входит в зацепление через шаг после предыдущего.

27. Схематично покажите, как изменяется форма зуба и его толщины по окружностям впадин и выступов при увеличении смещения исходного производящего контура.

Ответ: вверху – тоньше, внизу – толще, по делительной окружности – одинаково.

28. Для точки эвольвенты колеса покажите радиус кривизны профиля в этой точке, угол профиля, угол давления и инволюту.

Ответ: все, кроме угла давления, уже было. Угол давления определяется как угол между скоростью (трансверс.) и силой (общая нормаль).

29. Найдите на профиле зуба колеса точку, сопряженную с заданной точкой на профиле зуба шестерни. Определите скорость скольжения точки колеса.

Ответ: скорость скольжения точки определяется из векторного уравнения, связывающего скорость этой точки в абсолютном движении и скорость движения точки контакта.

30. По чертежу (или части чертежа) зубчатого зацепления определите передаточное отношение, модель, смещения и коэффициент торцевого перекрытия.

Ответ: все уже было.

31. Если на чертеже зубчатого зацепления уменьшить радиус окружности вершин одного из колес, будет ли работать такая передача? По какому параметру это можно определить.

Ответ: передача будет работать, если коэффициент торцевого перекрытия будет больше допускаемого значения.

32. Найдите по чертежу зубчатого зацепления максимальное и минимальное значения скорости скольжения профилей для одного из колес.

Ответ: скорость скольжения тем больше, чем больше угол между центрами колес. Vск=O1D*ω1, где O1D – расстояние от оси вращения до точки пересечения прямой, проходящей через другую ось и точку контакта с прямой, проходящей через эту ось и параллельную общей нормали в точке контакта.

33. Определите по чертежу станочного зацепления торцевой коэффициент перекрытия.

Ответ: то же, что и для шестерней.

34. Рассчитайте число избыточных связей в планетарном механизме при значении К=1;2;3.

Ответ: зубчатое зацепление считать парой 4-го класса.

35. На сателлите задайте точку М и определите вектор ее скорости.

Ответ: нарисовать ЛРС, а затем – теорема подобия.

Лист 4

1. Расскажите о назначении и основных этапах синтеза кулачкового механизма. В каких пределах изменяется угол давления и почему введено ограничение на его значение:

Ответ: Кулачковые механизмы используются для передачи движения на толкатель по строго определенному закону. В исследуемой установке кулачковый механизм используется для дозирования сыпучего груза. Угол давления изменяется от нуля минус допускаемого угла давления до плюс угла (40 градусов). Угол давления ограничивают во избежание заклинивания: чем больше угол давления, тем больше реакция в направлении, перпендикулярном движению толкателя, тем больше сила трения.

2. Какие размеры механизма влияют на величину угла давления в спроектированном кулачковом механизме? Возможно ли заклинивание выходного звена, и при каких условиях это происходит?

Ответ: величина зависит от передаточной функции, длины кривошипа толкателя, радиуса начальной шайбы и от эксцентриситета (для поступательно движущегося кулачка). Заклинивание возможно, если угол давления превышает допускаемое значение.

3. Поясните алгоритм определения основных размеров кулачкового механизма. Покажите области дозволенных положений оси вращения кулачка относительно фазовой кривой перемещение – скорость выходного звена при трех случаях вращения кулачка: только по часовой стрелке, только против часовой стрелки, реверсивный режим вращения.

Ответ: первоначально необходимо определить межосевое расстояние. Для этого нужно построить фазовый портрет по следующей схеме: от дуги на расстоянии, равном длине кривошипа, от начала координат откладываем первую кинематическую функцию (предварительно отложив по этой дуге величину линейного перемещения толкателя).

4. Расскажите о геометрической интерпретации кинематической передаточной функции скорости движения толкателя. В каких единицах она выражается? Покажите график изменения этой функции. Как вычисляли масштабы по обеим координатным осям?

Ответ: см. вопрос 10.Имеет размерность длины.

5. Расскажите о методике расчета координат центрового и конструктивного профилей кулачка. Как эти координаты находят при графическом методе синтеза кулачкового механизма?

Ответ: от центровой шайбы откладывают соответствующие дуги. Подробно прочитать про кси. Далее – строим на полученной кривой окружности, соответствующие различным положениям толкателя и проводим к ним огибающую.

6. Поясните алгоритм вычислений основных размеров кулачкового механизма с использованием ЭВМ.

Ответ: разобраться в методе, конечно, можно, но самый простой способ следующий:

1. Переводим полярные координаты угловых точек в декартовы.

2. В результате получаем точки, через которые должны проходить лучи, отсекающие область решений. Угловые коэффициенты можно получить из допустимого угла давления и угла из полярных координат.

3. Решаем систему из двух уравнений и получаем координаты оси вращения кулачка.

4. Данный метод также можно использовать при переборе точек.