1.Показова функція

Рівняння показової функції має вигляд: або . Невідомі коефіцієнти а та b, що входять до емпіричної формули, визначаються за формулами :

;

Наприклад, у результаті обчислень отримали lg a = 0.6789, а lg b = 0,03216, звідки знайшли, що а = 4,77; b = 1,08. Тоді емпірична формула буде мати вигляд: у = 4,77 * 1,08^х.

Знаходимо теоретичне значення апроксимованої кривої за формулою:

lg y_i = lg a + x_i lg b = 0.6789 + x_i *0.03216

де x_i - експериментальне значення і -го досліду.

2.Степенева функція

Рівняння степеневої функції має вигляд: у = ах^b або lg у = lg а + b lgx

Невідомі коефіцієнти а та b, що входять до емпіричної формули, визначаються за формулами :

Подальший порядок проведення розрахунків аналогічний порядку п.1 (показова функція).

3.Логарифмічна функція

Рівняння логарифмічної функції має вигляд: y= a + b lg x.

Невідомі коефіцієнти а та b, що входять до емпіричної формули можуть визначаються за формулами :

;

Подальший порядок проведення розрахунків невідомих коефіцієнтів а та b аналогічний порядку п.1 (показова функція).

Коефіцієнти та сталі, які входять до останніх емпіричних формул визначаються із системи нормальних рівнянь, отриманих способом найменших квадратів і наведених в табл. 1.

Вихідне рівняння	Система нормальних рівнянь

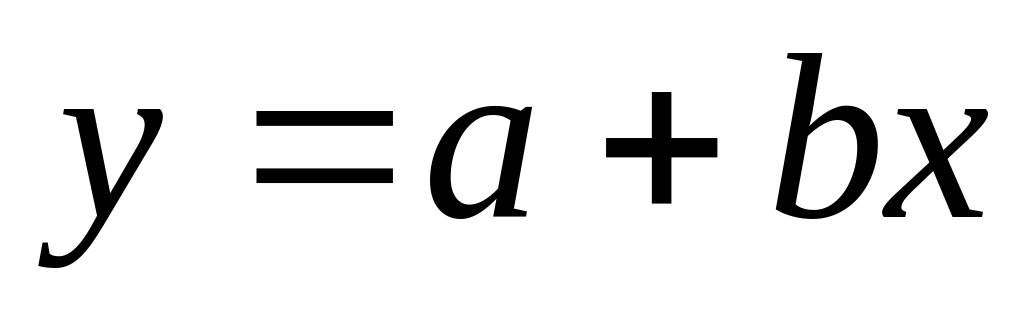
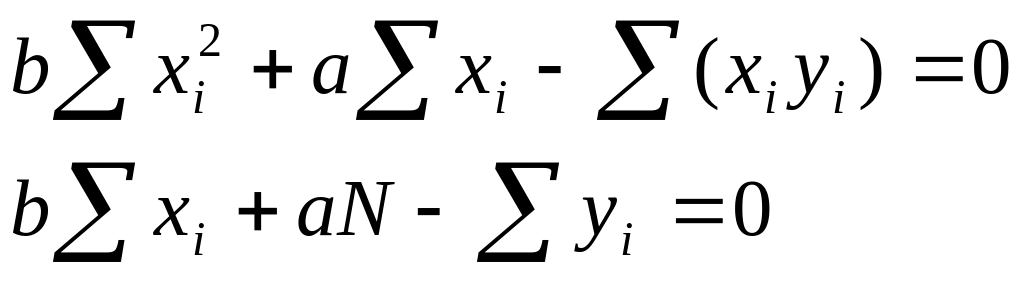
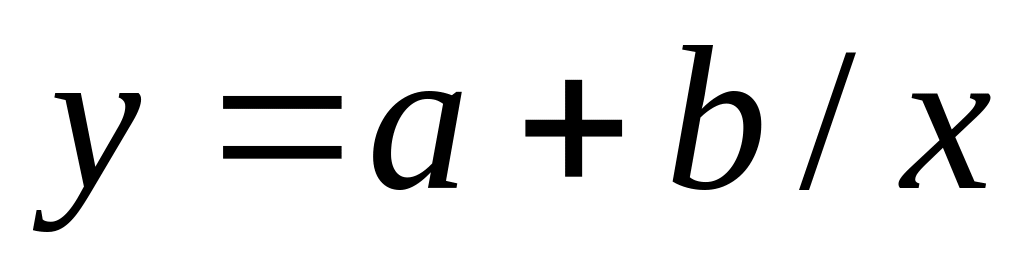
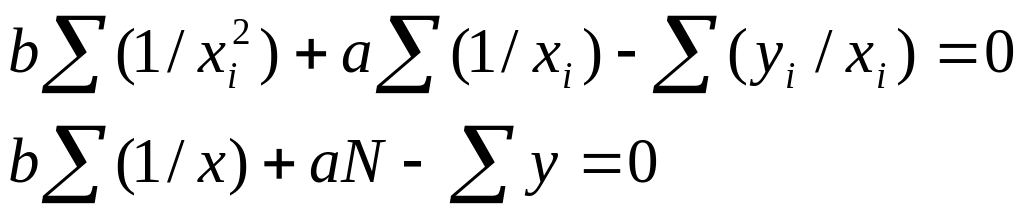
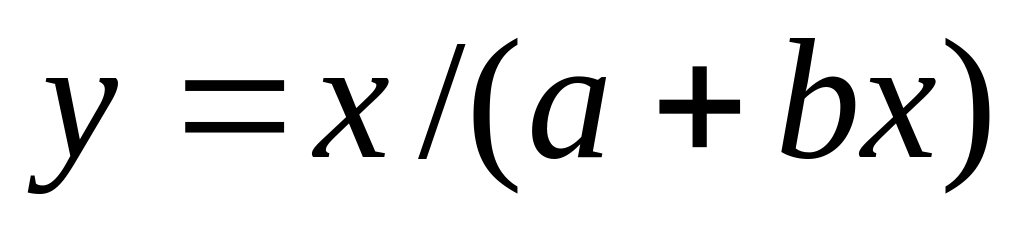
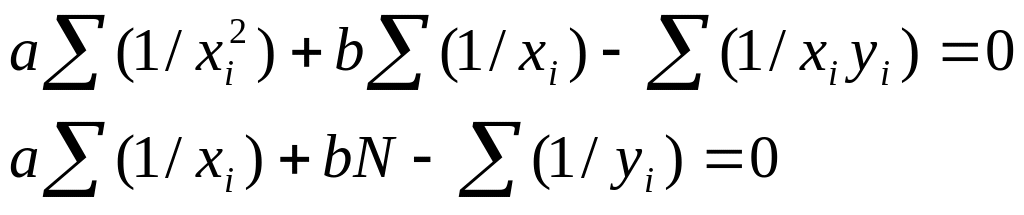
Знак , наведений у формулах таблиці дня визначення невідомих коефіцієнтів а та b, означає суму експериментальних значень (вихідних даних для проведення розрахунків) від і = 1 до N, де і - порядковий номер досліду в експерименті; N - кількість проведених повторностей (дослідів) в експерименті.

Розв'язати систему нормальних рівнянь відносно невідомих коефіцієнтів а та b можна виконати будь- яким загальноприйнятим способом.

При виконанні першого етапу може виникнути такий випадок , що для апроксимації експериментальних даних за своєю графічною побудовою (виглядом) орієнтовно підходять дві чи три функції. Тому для оцінки ступеня точності вирівнювання (апроксимації), побудованої графічної залежності за результатами отриманих експериментальних даних, тією чи іншою вибраною апроксимуючою функцією, необхідно визначити величину так званої "нев'язки" , тобто сумарне середньоквадратичне відхилення теоретичних значень, обчислених за визначеною емпіричною формулою від експериментальних значень проведеного досліду для кожної з вибраних для проведення апроксимації формул. Величина "нев'язки" визначається за формулою:

де - експериментальні значення і-го досліду;

- теоретичне значення і-го досліду, визначеного за одержаною емпіричною формулою.

Для подальшого використання залишають те емпіричне рівняння, для якого величина "нев'язки" найменша за числовим значенням, де знак означає суму квадратів від і = 1 до N, де .

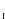Приклад. Підібрати емпіричну формулу для такого масиву експериментальних даних, де кількість повторностей в експерименті дорівнює 8.

x	1	2	3	4	5	6	7	8
y	10	16	20	25	30	35	50	80

Наносимо точки експериментальних даних на координатні осі і будуємо ламану лінію, тобто графік експериментальної залежності (рис 3).

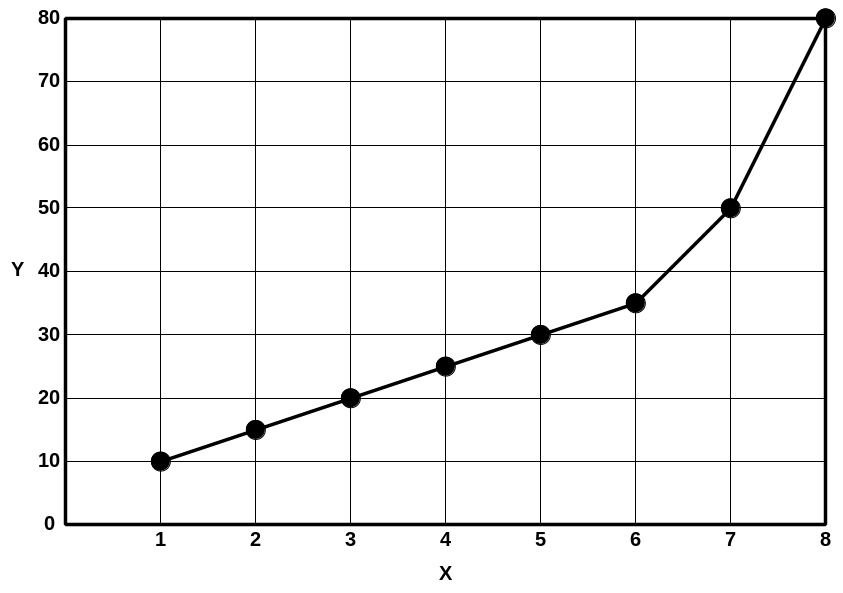
Рис 3. Експериментальна залежність

Орієнтовно, для описання поведінки побудованих експериментальних точок (експериментального масиву даних) обираємо дві функції: лінійну виду та другого порядку , тобто відповідно пряму лінію та параболу. Після визначення методом найменших квадратів невідомих коефіцієнтів а, b, та с, що входять до цих формул, записуємо одержані емпіричні формули:

;

Перевіримо, яка з одержаних емпіричних формул та , краще апроксимує (описує, вирівнює) побудовану експериментальну залежність, наведену на рис. 3. Для цього визначимо показники, які наведені в табл. 2, і занесемо до неї результати цих обчислень.