5. Взаємне розташування двох прямих в просторі.

Розкрити зміст поняття «взаємне розташування прямих в просторі». Розкрити порядок визначення взаємного положення прямих в просторі, ґрунтуючись на означенні кута між двома векторами. Приклади.

Н ехай є дві прямі і . У просторі дві прямі можуть бути мимобіжними, паралельними, перетинатися, співпадати.

1. Мимобіжні прямі. Це можливо тоді, коли вектори , , не можуть лежати в одній площині, тобто вони – лінійно незалежні, а отже визначник складений з координат векторів повинен дорівнювати нулю.

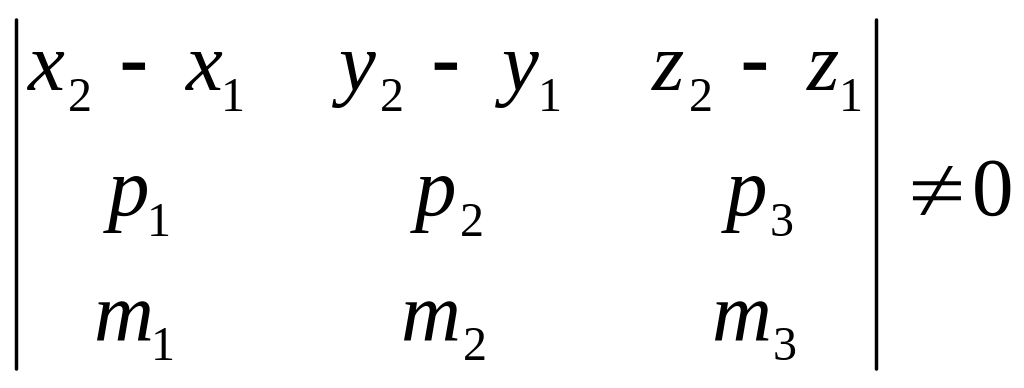(11.5)

2. Прямі, що перетинаються. Це можливо тоді, коли вектори , , лежать в одній площині, але . Тоді вектор можна розкласти за векторами . А тому вектор є лінійною комбінацією векторів : , з чого випливає, що вектори – лінійно залежні, а отже визначник складений з координат векторів повинен дорівнювати нулю.

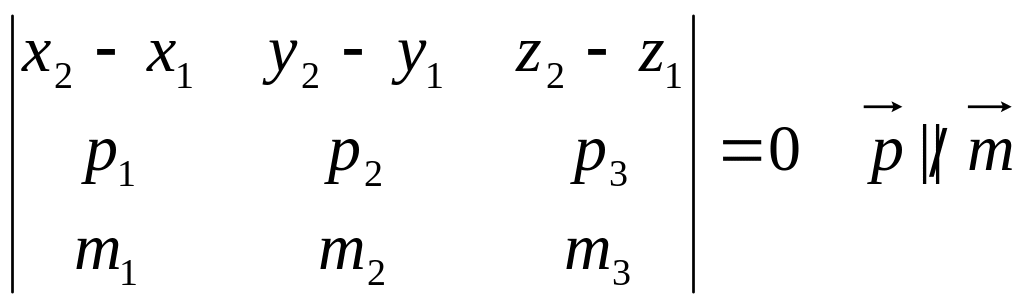(11.6)

3. Паралельні прямі. Це можливо тоді, коли вектори , паралельні між собою, але не паралельні вектору .

(11.7)

3. Прямі, що співпадають. Це можливо тоді, коли вектори , , паралельні між собою.

(11.8)

6. Взаємне розташування прямої та площини в просторі.

Р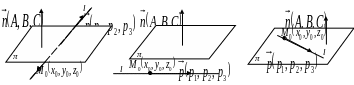 озкрити порядок визначення взаємного положення прямої та площини в просторі, ґрунтуючись на означенні кута між двома векторами. Приклади.

Нехай є пряма і площина . У просторі пряма може перетинати площину, бути паралельною площині, або належати площині.

1. Перетин прямої і площини. Це можливо тоді, коли вектори , не є перпендикулярними, тобто скалярний добуток векторів не дорівнює нулю.

(11.9)

2. Паралельність прямої і площини. Це можливо тоді, коли вектори , є перпендикулярними, тобто скалярний добуток векторів дорівнює нулю. Але жодна точка прямої не належить площині, тобто точка не задовольняє рівняння площини.

(11.10)

3. Пряма належить площині. Це можливо тоді, коли вектори , є перпендикулярними, тобто скалярний добуток векторів дорівнює нулю. Та всі точки прямої належать площині, тобто точка задовольняє рівняння площини.

(11.11)

7. Кут між двома прямими.

Нехай є дві прямі і .

(11.12)

8. Кут між прямою та площиною.

Н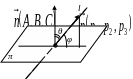 ехай є пряма і площина .

(11.13)