2.4. Рівняння площини через три не колінеарні точки.

Точки, що лежать на одній прямій називаються колінеарними.

Н ехай площина проходить через не колінеарні точки , і . В якості векторів , візьмемо вектори , , які є неколінеарними. Підставивши в рівняння 10.3., отримаємо:

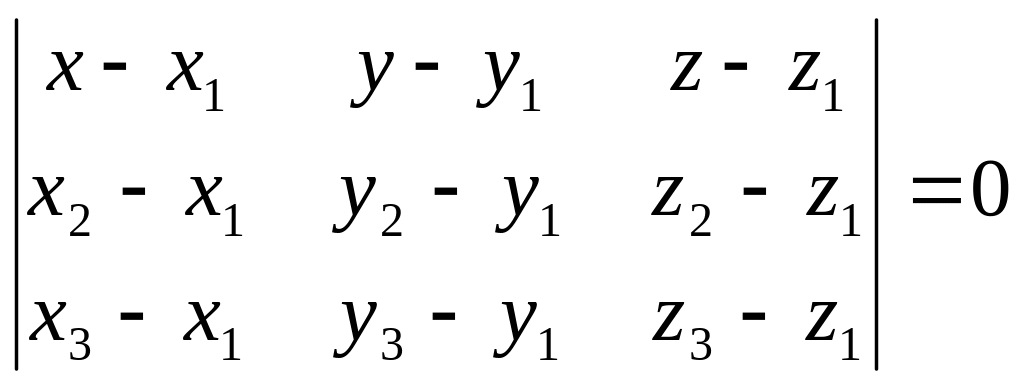(10.4)

Рівняння 10.4. називається рівнянням площини через три не колінеарні точки.

2.5. Рівняння площини у відрізках.

Н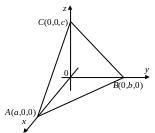 ехай площина перетинає вісь абсцис в точці , вісь ординат в точці , вісь аплікат в точці . Ці точки не колінеарні. Запишемо рівняння площини через три точки 10.4.

;

;

; ;

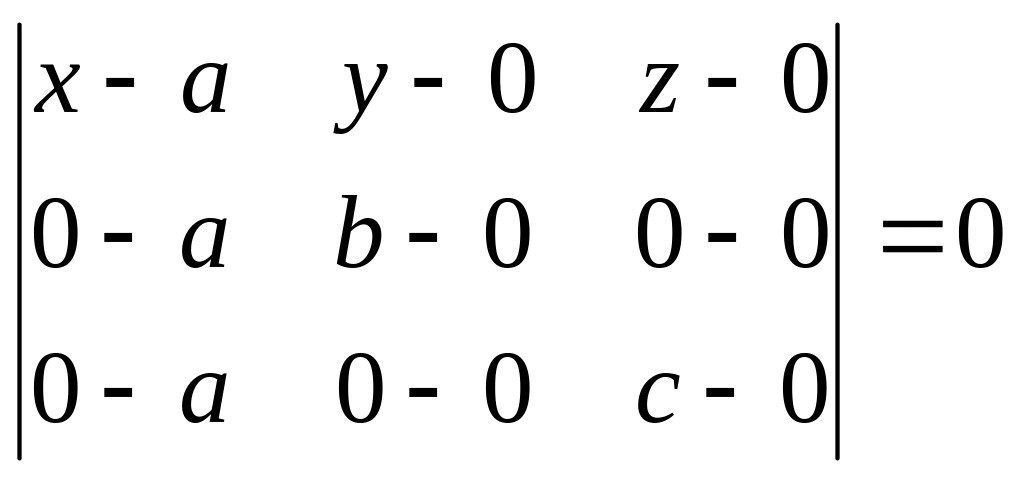(10.5)

Рівняння 10.5. називається рівнянням площини у відрізках.

2.6. Розташування площини відносно системи координат.

З’ясуємо як розташовується площина відносно осей координат.

1. Нехай . Тоді , вектор нормалі , бо . , тому .

2. Нехай . Тоді , , тому .

3. Нехай . Тоді , вектор нормалі , бо . , тому .

4. Нехай . Тоді , , тому .

5. Нехай . Тоді , вектор нормалі , бо . , тому .

6. Нехай . Тоді , , тому .

7. Нехай . Тоді , вектор нормалі , бо . , тому .

8. Нехай . Тоді . , , тому .

9. Нехай . Тоді , вектор нормалі , бо . , тому .

10. Нехай . Тоді . , , тому .

11. Нехай . Тоді , вектор нормалі , бо . , тому .

12. Нехай . Тоді . , , тому .

13. Нехай . Тоді . , площина проходить через початок координат.

3. Умови паралельності та перпендикулярності площин. Відстань від точки до площини.

3.1. Умова паралельності площин.

Нехай площини задані в загальному вигляді та .

(10.6)

Дві площини паралельні тоді і тільки тоді, коли відповідні коефіцієнти при змінних х, у, z пропорційні.

3.2. Умова перпендикулярності площин.

Н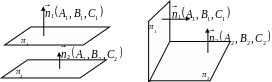 ехай площини задані в загальному вигляді та .

(10.7)

Дві площини перпендикулярні тоді і тільки тоді, коли сума добутків відповідних коефіцієнти при змінних х, у, z дорівнює нулю.

3.3. Відстань від точки до площини.

Означення 10.2. Довжина перпендикуляра, проведеного з точки на площину називається відстанню від цієї точки до площини. Якщо точка належить площині, то відстань дорівнює нулю.

Нехай задані площина в загальному вигляді і точка . Відстань від точки до площини знаходиться аналогічно як відстань від точки до прямої. В результаті отримаємо:

(10.8)

3.4. Відстань між двома паралельними площинами.

Нехай площини задані в загальному вигляді та .

Візьмемо точку на площині . . . Підставимо в 10.8

(10.9)

3.5. Кут між двома площинами.

Нехай площини задані в загальному вигляді та .

(10.10)

4. Рівняння прямої в просторі, їх різновиди.

4.1. Рівняння прямої як перетин двох площин.

Нехай площини задані в загальному вигляді та . З курсу стереометрії відомо що, якщо дві площини мають спільну точку, то вони перетинаються по прямій. Іншими словами довільні дві непаралельні площини задають пряму. Тобто якщо (не виконується умова паралельності), то

(11.1)

Рівняння 11.1. називається рівнянням прямої як перетин двох площин.

4.2. Канонічне рівняння прямої.

Н ехай пряма проходить через точку і паралельна вектору . Візьмемо на прямій довільну точку . Тоді вектор . А тому координати векторів повинні бути пропорційними.

(11.2)

Рівняння 11.2. називається рівнянням прямої через точку і напрямний вектор або канонічним рівнянням прямої.

4.3. Рівняння прямої через дві точки.

Н ехай пряма проходить через точки і . В якості вектора візьмемо вектор , який паралельний прямій l, а тому і вектору . Підставивши в рівняння 11.2., отримаємо:

(11.3)

Рівняння 11.3. називається рівнянням прямої через дві точки.

4.4. Параметричне рівняння прямої.

Нехай пряма l задається рівнянням 11.2. Введемо параметр t наступним чином . Тоді прирівнявши кожен дріб, маємо систему:

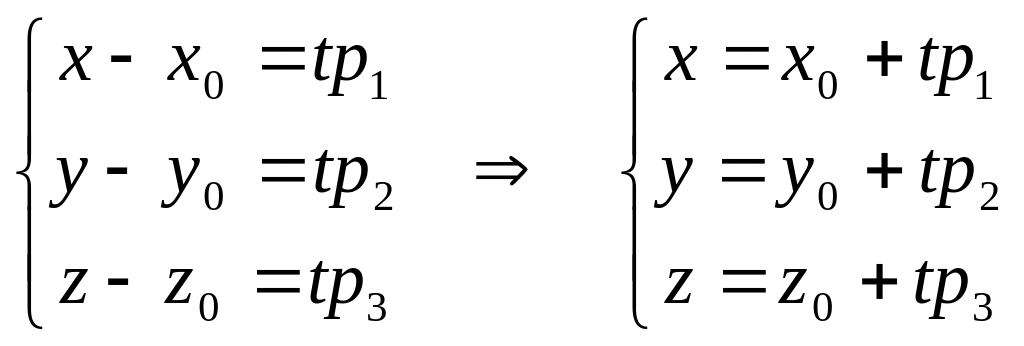(11.4)

Рівняння 11.4. називається параметричним рівнянням прямої.

4.5. Розташування прямої відносно системи координат.

З’ясуємо як розташовується пряма відносно осей координат.

1. Нехай . Тоді напрямний вектор , бо . Тому . А оскільки , то .

2. Нехай . Тоді напрямний вектор , бо . Тому . А оскільки , то .

3. Нехай . Тоді напрямний вектор , бо . Тому . А оскільки , то .

4. Нехай . , , тоді (пряма, що паралельна двом площинам, паралельна і прямій, по якій вони перетинаються). Або це доводиться так: напрямний вектор , бо , тому .

5. Нехай . , , тоді . Або напрямний вектор , бо , тому .

6. Нехай . , , тоді . Або напрямний вектор , бо , тому .