11

Модуль 2. Аналітична геометрія та вступ до математичного аналізу

Тема 5. Лінії на площині.

1. Системи координат на площині.

П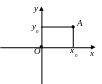 роведемо на площині через точку О дві взаємно перпендикулярні прямі х та у – вісі координат. Вісь х називається віссю абсцис, а вісь у – віссю ординат. Точка перетину О – початком координат.

На віссях координат відмітимо масштаб – одиничний відрізок.

Кожній точці А площини співставимо пару чисел – координати точки – абсцису (х₀) та ординату (у₀). Точки вісі абсцис мають рівні нулю ординати у=0, а точки вісі ординат мають рівні нулю абсциси х=0. Початок координат О(0, 0).

Означення 8.1. Побудовану таким способом систему координат називають декартовою.

2. Рівняння лінії на площині.

Нехай на площині задана лінія (крива). Координати х та у точки, що лежить на лінії, не можуть бути довільними, а повинні бути якимось-чином пов’язані. Такий зв’язок записується у вигляді рівняння.

Означення 8.2. Рівнянням кривої на площині називається рівняння , якщо координати будь-якої точки кривої задовольняють це рівняння, а координати точки, що не лежить на кривій, не задовольняє це рівняння.

Приклад. 8.1. Нехай є крива і точки , , , . Які точки належать прямій?

: – точка належить лінії.

: – точка не належить лінії.

3. Рівняння прямої на площині, їх різновиди.

3.1. Рівняння прямої з кутовим коефіцієнтом.

Н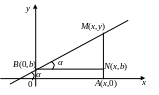 ехай пряма перетинає вісь ординат в точці і утворює з віссю абсцис кут α. Візьмемо на прямій довільну точку . Тоді тангенс кута α нахилу прямої знайдемо з прямокутного трикутника MBN: . – називається кутовим коефіцієнтом прямої.

(8.1)

Рівняння 8.1. називається рівнянням прямої з кутовим коефіцієнтом.

3.2. Рівняння прямої через точку і кутовий коефіцієнт.

Нехай пряма проходить через точку і утворює з віссю абсцис кут α. Так як лежить на прямій, то її координати задовольняють рівняння 8.1., тобто .

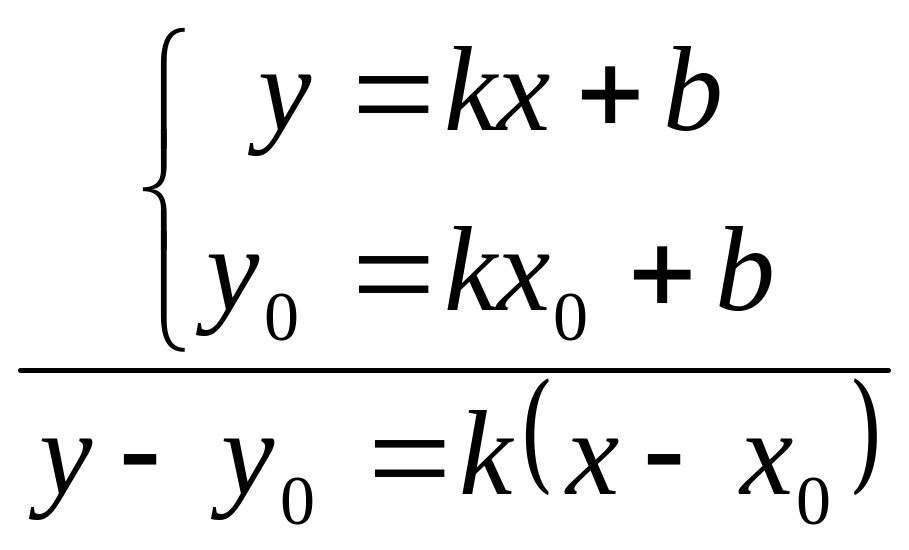
(8.2)

Рівняння 8.2. називається рівнянням прямої через точку і кутовий коефіцієнт.

3.3. Рівняння прямої через точку і напрямний вектор.

Н ехай пряма проходить через точку і паралельна вектору . Візьмемо на прямій довільну точку . Тоді вектор . А тому координати векторів повинні бути пропорційними.

(8.3)

Рівняння 8.3. називається рівнянням прямої через точку і напрямний вектор.

3.4. Рівняння прямої через дві точки.

Н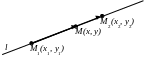 ехай пряма проходить через точки і . В якості вектора візьмемо вектор , який паралельний прямій l, а тому і вектору . Підставивши в рівняння 8.3., отримаємо:

(8.4)

Рівняння 8.4. називається рівнянням прямої через дві точки.

3.5. Рівняння прямої у відрізках.

Н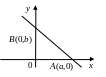 ехай пряма перетинає вісь абсцис в точці , вісь ординат в точці . Запишемо рівняння прямої через дві точки 8.4.

; ;

(8.5)

Р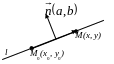 івняння 8.5. називається рівнянням прямої у відрізках.

3.6. Рівняння прямої через точку і нормальний вектор.

Вектор , перпендикулярний до прямої l, називається нормальним.

Нехай пряма проходить через точку і перпендикулярна вектору . Візьмемо на прямій довільну точку . Тоді вектор . А тому їх скалярний добуток дорівнює нулю.

(8.6)

Рівняння 8.6. називається рівнянням прямої через точку і нормальний вектор.

3.7. Загальне рівняння прямої, її розташування.

В рівнянні 8.6. розкриємо дужки і позначимо вираз . Отримали рівняння.

(8.7)

Рівняння 8.7. називається загальним рівнянням прямої. Коефіцієнти є координатами нормального вектора . Причому коефіцієнти не можуть дорівнювати нулю одночасно.

З’ясуємо як розташовується пряма відносно осей координат.

1. Нехай . Тоді , . Всі точки прямої мають однакову ординату , тому .

2. Нехай . Тоді , . Це вісь абсцис, тому .

3. Нехай . Тоді , . Всі точки прямої мають однакову абсцису , тому .

4. Нехай . Тоді , . Це вісь ординат, тому .

5. Нехай . Тоді . Пряма проходить через початок координат.