1) Недопустимо смешивать понятия «методика исс л е д о в а н и я » и «м е т о д ы и с с л е д о в а н и я » . М е тодика исследования — это своеобразная программа-план исследования в целом, результат всесторонней предварительной разработки той или иной темы изучения, проблемы. Методы исследования — это пути, способы получения тех или иных данных.

Любое конкретное исследование может быть представлено в виде ряда этапов.

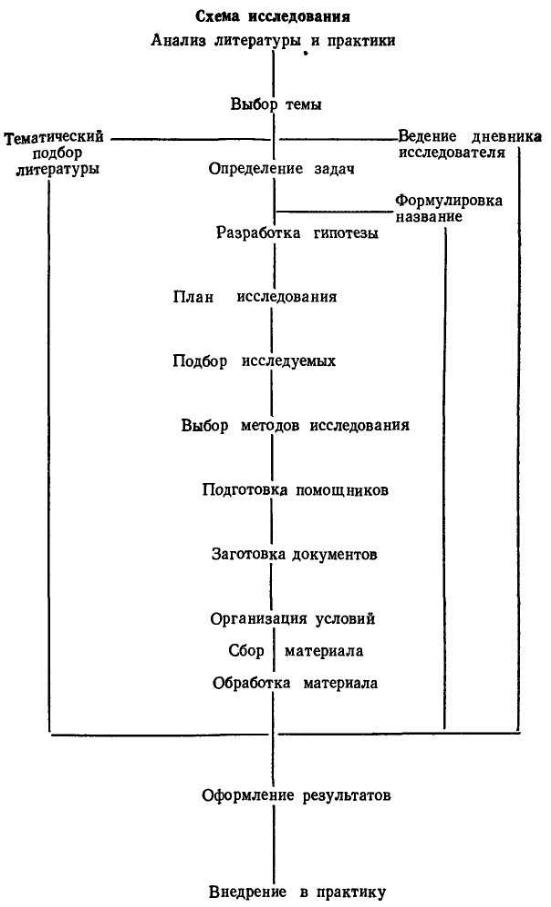
2) Экспериме́нт - метод исследования некоторого явления в управляемых условиях. Отличается от наблюдения активным взаимодействием с изучаемым объектом. Обычно эксперимент проводится в рамках научного исследования и служит для проверки гипотезы, установления причинных связей между феноменами.

Особенности:

• исследователь сам вызывает изучаемое явление, а не ждёт когда оно произойдет;

• может изменять условия протекания изучаемого процесса;

• в эксперименте можно попеременно исключать отдельные условия с целью установить закономерные связи;

• эксперимент позволяет варьировать количественное соотношение условий и осуществлять математическую обработку данных.

3) Статистические данные должны быть представлены так, чтобы ими можно было пользоваться. Существует 3 основных формы представления статистических данных:

Текстовая – включение данных в текст;

Табличная – представление данных в таблицах;

Графическая – выражение данных в виде графиков.

9) Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. Остальное в тетради хуесосы.

10) Средние величины делятся на два больших класса: степенные средние и показатели вариации

Степенные средние:

• Арифметическая

• Гармоническая

• Геометрическая

• Квадратическая

Вопрос о выборе средней решается в каждом отдельном случае, исходя из задач исследования и наличия исходной информации.

Средняя арифметическая простая используется в тех случаях, когда варианты или варьирующие признаки встречаются только по одному разу и имеют одинаковый вес в совокупности. Средняя арифметическая взвешенная используется, когда данные сгруппированы, а отдельные значения признака встречаются неодинаковое число раз.

Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Средняя гармоническая вычисляется в тех случаях, когда в качестве весов применяются не единицы совокупности, а произведения этих единиц на значения признака (то есть М=х×f).

Средняя гармоническая простая исчисляется в тех случаях, когда веса одинаковы, то есть равны между собой.

Средняя геометрическая простая используется при вычислении среднего коэффициента роста (темпа роста) в рядах динамики.

Средняя квадратическая Основной сферой ее применения является измерение вариации признака в совокупности)

Применение средней квадратической: 1) используется для расчета среднего квадратического отклонения 2) когда величины входящие в исходные данные представлены в виде квадратных функций 3) рассматриваемое движение ВС в воздушном пространстве по глиссаде, т.е. измеряется в каждый момент времени отклонения по высоте и курсу 4) используется для расчетов темпа роста (динамики) какого либо показателя.

11) Корреляция позволяет находить статистически достоверные количественные меры связи в тех случаях, когда какому-либо одному фактору соответствует не одно, а несколько значений какого-либо другого фактора, причем варьирующих в каких-то пределах. Связь в этом случае будет выражаться в средних значениях, полученных на целом ряде изменений.

Линейный коэффициент корреляции  характеризует существование линейной связи между двумя величинами. Если связь криволинейная то он не будет работать.

Различают корреляции нескольких направлений:

прямая положительная корреляция , при которой увеличение причинного фактора вызывает увеличение следственного фактора

прямая отрицательная к о р р е л я ц и я , при которой уменьшение причинного фактора вызывает уменьшение следственного фактора

о б р а т н а я п о л о ж и т е л ь н а я к о р р е л я ц и я ,при которой уменьшение причинного фактора вызывает увеличение следственного фактора

о б р а т н а я о т р и ц а т е л ь н а я к о р р е л я ц и я , при которой увеличение причинного фактора вызывает уменьшение следственного фактора

Математическое значение корреляции выражается ее коэффициентом от— 1 (максимальной отрицательной связи) до +1 (максимальной положительной связи)

12) Выборочный метод основывется на законе больших чисел. В силу этого закона совокупное действие большого числа случайных факторов приводит (при некоторых

весьма общих условиях) к результату, почти не зависящему от случая. Следовательно, с одной стороны, закон больших чисел означает, что закономерности массовых однородных

явлений проявляются лишь на достаточно большом количестве лиц (или показателей) и могут быть выражены только в форме средних величин; с другой стороны, при опоре на действие закона больших чисел оказывается возможным освободить от влияния случая соответствующие статистические показатели. Закон обусловливает взаимопогашение случайных отклонений и позволяет обнаружить в массе явлений свое объективное действие. При выборочном методе изучаются не все единицы той или иной совокупности, а лишь отобранная их часть. При этом обобщенные характеристики отобранной части (выборочной Совокупности) распространяются на всю совокупность (генеральную совокупность). Для установления фактов выборочный метод позволяет проводить вместо сплошного исследования(всего контингента отобранных лиц) несплошное исследование (части этого контингента).

15) Средние величины делятся на два больших класса: степенные средние и показатели вариации

Степенные средние:

• Арифметическая

• Гармоническая

• Геометрическая

• Квадратическая

Вопрос о выборе средней решается в каждом отдельном случае, исходя из задач исследования и наличия исходной информации.

Средняя арифметическая простая используется в тех случаях, когда варианты или варьирующие признаки встречаются только по одному разу и имеют одинаковый вес в совокупности. Средняя арифметическая взвешенная используется, когда данные сгруппированы, а отдельные значения признака встречаются неодинаковое число раз.

Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Средняя гармоническая вычисляется в тех случаях, когда в качестве весов применяются не единицы совокупности, а произведения этих единиц на значения признака (то есть М=х×f).

Средняя гармоническая простая исчисляется в тех случаях, когда веса одинаковы, то есть равны между собой.

Средняя геометрическая простая используется при вычислении среднего коэффициента роста (темпа роста) в рядах динамики.

Средняя квадратическая Основной сферой ее применения является измерение вариации признака в совокупности)

Применение средней квадратической: 1) используется для расчета среднего квадратического отклонения 2) когда величины входящие в исходные данные представлены в виде квадратных функций 3) рассматриваемое движение ВС в воздушном пространстве по глиссаде, т.е. измеряется в каждый момент времени отклонения по высоте и курсу 4) используется для расчетов темпа роста (динамики) какого либо показателя.

17) Квадратный корень из дисперсии, равный sigma, называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.

1°. Дисперсия постоянной равна нулю.   2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

3°. Если   и   - независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий:

  Средним квадратическим отклонением   случайной величины   называется корень квадратный из ее дисперсии

1) вычисляется разность между каждой срединной

вариантой и средней арифметической величиной (напри

мер, 1—5,6= - 4,6); вычисленный таким образом пока

затель условно обозначается буквой «с?»;

2) чтобы избежать числовых операций с положи

тельными и отрицательными величинами, все получен

ные разности возводятся в квадрат (например, —4,62=

= 21,16);

3) вычисляется произведение каждого квадрата раз

ности на его частоту (например, 21,16x28=592,48);

4) вычисляется сумма всех полученных произведений

квадратов разностей и их частот (в нашем примере она

равняется 2270,72);

5) вычисляется среднее квадратическое отклонение

по формуле:

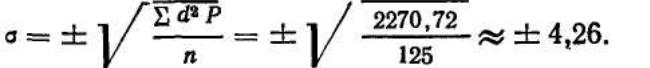
18) Правило трёх сигм ( ) — практически все значения нормально распределённой случайной величины лежат в интервале  . Более строго — приблизительно с 0,9973 вероятностью значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина   истинная, а не полученная в результате обработки выборки).

20) Выборочная совокупность - часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение о всей генеральной совокупности.

Для того, чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность выборка должна обладать свойством репрезентативности.

Генеральная совокупность - вся изучаемая выборочным методом статистическая совокупность объектов и/или явлений общественной жизни, имеющих общие качественные признаки или количественные переменные.

Генеральная совокупность состоит из всех единиц, которые могут быть к ней отнесены. Обычно ее рассматривают как приближающуюся к бесконечности совокупность.

22) Под малой выборкой понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Объем малой выборки обычно не превышает 30 единиц и может доходить до 4 — 5 единиц.

Средняя ошибка малой выборки   вычисляется по формуле: , где   — дисперсия малой выборки.

23) Функциональная связь отражает четкую однозначную зависимость, при которой изменение какого-либо одного фактора неизбежно приводит к однозначному изменению

другого. Корреляция ЖЕ позволяет находить статистически достоверные количественные меры связи в тех случаях, когда какому-либо одному фактору соответствует не одно, а неcколько значений какого-либо другого фактора, причем варьирующих в каких-то пределах. прямая положительная корреляция, при

которой увеличение причинного фактора вызывает увеличение следственного фактора

прямая отрицательная корреляция, при которой уменьшение причинного фактора вызывает уменьшение следственного фактора обратная положительная корреляция, при которой уменьшение причинного фактора вызывает

увеличение следственного фактора обратная отрицательная корреляция ,

при которой увеличение причинного фактора вызывает уменьшение следственного фактора

24) Значимость коэффициента корреляции определяется по формуле: 

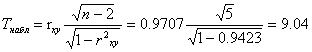
Для оценки значимости коэффициента корреляции используют критерий Стьюдента. По таблице Стьюдента находим T_таблT_табл.Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически - значим.