28

	Кафедра информационных технологий проектирования летательных аппаратов
Конспект лекций: СОВРЕМЕННЫЕ МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ ПРОЕКТИРОВАНИЯ

Продолжение Темы 4. Темы 5, 6

Табличный симплекс метод

Пример 1

Фирма производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.

Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В - 4 м².

Фирма может получить от своих поставщиков до 1700 м² досок в неделю.

Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В - 30 мин. В неделю можно использовать 160 ч машинного времени. Сколько изделий каждой модели следует фирме выпускать в неделю, если каждое изделие модели А приносит 2 дол. прибыли, а каждое изделие модели В - 4 дол. прибыли?

(1)

(для досок),

(для машинного времени) (2)

Следовательно, задача состоит в том, чтобы найти значения x₁ и x₂, удовлетворяющие условиям неотрицательности (1) и ограничениям типа неравенства (2) и максимизирующие функцию

z = 2x₁ + 4x₂.

В стандартной форме с неотрицательными дополнительными переменными ограничения и целевая функция принимают вид

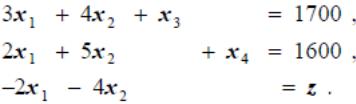
Решим поставленную задачу линейного программирования табличным симплекс-методом.

Составим симплекс таблицу

Отрицательные коэффициенты в целевой функции свидетельствуют о том, что оптимальное решение не достигнуто.

Итерация 1. Продолжим поиск оптимального решения. Для этого попробуем внести в базис переменную х₂ Т.к. базисная переменная должна иметь коэффициент 1, разделим уравнение (ограничение) с большим коэффициентом при х₂ на этот коэффициент, т.е. разделим второе ограничение на 5. Получим

(3)

Далее, для того чтобы удалить переменную х₂ из первого ограничения, умножим уравнение (3) на коэффициент при переменной х₂ в первом ограничении, т.е. на 4, а затем вычтем из первого ограничения. Получим

Для того чтобы удалить переменную х₂ из целевой функции, умножим уравнение (3) на коэффициент при переменной х₂ в целевой функции, т.е. на -4, а затем вычтем из целевой функции. Получим

Составим симплекс таблицу для итерации 1

Т.к. в целевой функции остался отрицательный коэффициент, продолжим поиск оптимального решения.

Итерация 2. Внесем в базис переменную х₁ Т.к. базисная переменная должна иметь коэффициент 1, разделим уравнение (ограничение) с большим коэффициентом при х₁ на этот коэффициент, т.е. разделим второе ограничение на 7/5. Получим

(4)

Далее, для того чтобы удалить переменную х₁ из второго ограничения, умножим уравнение (4) на коэффициент при переменной х₁ во втором ограничении, т.е. на 2/5, а затем вычтем из второго ограничения. Получим

Для того чтобы удалить переменную х₁ из целевой функции, умножим уравнение (4) на коэффициент при переменной х₂₁ в целевой функции, т.е. на -2/5, а затем вычтем из целевой функции. Получим

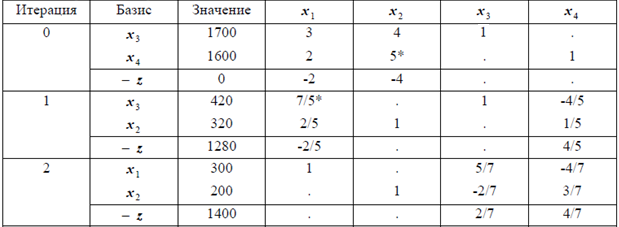
Составим симплекс таблицу для итерации 2

Т.к. коэффициенты в целевой функции положительны – найдено оптимальное решение.

Сводная симплекс таблица имеет вид:

Тема 5, 6. Постоптимальный анализ (Анализ моделей на чувствительность). Программные средства оптимизации (Microsoft Excel)

1. Обращение базиса и симплекс-множители.

2. Диапазоны устойчивости

3. Двойственный симплекс-метод

4. Решение оптимизационных задач с помощью Microsoft Excel

Постоптимальный анализ (анализ моделей на чувствительность) – это процесс, реализуемый после того, как оптимальное решение задачи получено. В рамках такого анализа выявляется чувствительность оптимального решения к определенным изменениям исходной модели. Иными словами, анализируется влияние возможных изменений исходных условий на полученное ранее оптимальное решение. Важность этого анализа ЗЛП объясняется также ещё и тем, что большая часть параметров ЗЛП точно не известна, и на практике обычно берутся приближенные значения параметров. Таким образом, нас интересуют такие диапазоны изменения этих параметров, в которых оптимальное решение остается оптимальным в том смысле, что не меняется базис.

Отсутствие методов, позволяющих выявить влияние возможных изменений параметров модели на оптимальное решение, может привести к тому, что полученное (статическое) решение устареет еще до своей реализации.

1. Обращение базиса и симплекс-множители.

Вспомним вид общей задачи ЛП в стандартной форме:

Минимизировать

при ограничениях

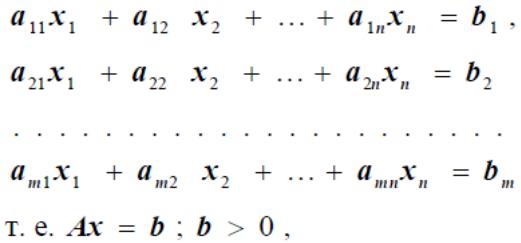(3.1)

Матрица A может быть разбита следующим образом:

A = ( BR) (3.2)

где B - матрица с коэффициентом на диагонали x₁ , x₂ ,… , x_m , a R – матрица размерностью m × n − m (остаток матрицы A ).

Запишем уравнение (3.1) в виде

( BR) x = b (3.3)

Канонический вид для некоторого базиса может быть получен умножением вектора исходных ограничении на матрицу, полученную обращением этого базиса. Таким образом, каноническая форма для базиса получается умножением уравнения (3.3) на матрицу В^-1.

B⁻¹ ( BR) x = B⁻¹b ,

Тогда получим соотношение

I_m( B^-1R) x =b^/ (это - уравнение (3.2а)) (3.4)

или

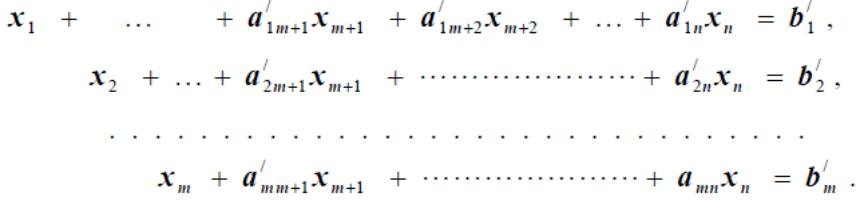(3.4б)

что соответствует канонической форме для ограничений. В (3.4) I_m – единичная матрица, b^/ = B⁻¹b

Если а_j — столбец из коэффициентов при переменной х_j в ограничении (3.1), то

(3.4а)

представляет собой столбец из коэффициентов при х_j в канонической форме для всех столбцов j = m+1,…, n.

В каждой канонической форме относящиеся к ней базисные переменные были исключены из целевой функции z. В симплекс-методе это делается итеративно, например на каждой стадии с использованием исходного вида ограничений (3.1).

Симплекс-множители

Можно умножить ограничения на π₁, π₂, …., π_m , прибавить к выражению для функции z и получить соотношение

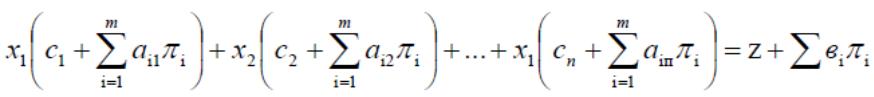(3.5)

Значения π_i можно выбрать так, что коэффициенты при базисных переменных в уравнениях (3.5) станут нулевыми. Значения π_i. называются симплекс-множителями. Если x₁, x₂,…,x_m- базисные переменные (при этом не происходит потери общности), то π_i определяются из системы уравнений

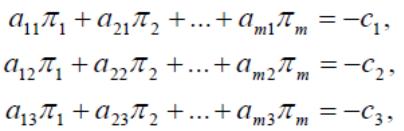
т.е. , (3.6)

где В^Т матрица из коэффициентов при базисных переменных, а - коэффициенты при базисных переменных в исходном виде для функции z. Так как

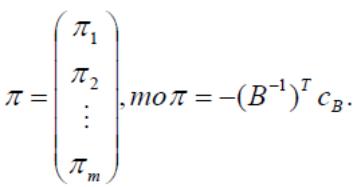(3.7)

Однако может быть, что значения π₁, … , π_m легче получить, просматривая симплекс-таблицы.

Рассмотрим снова таблицу примера 1 предыдущей лекции.

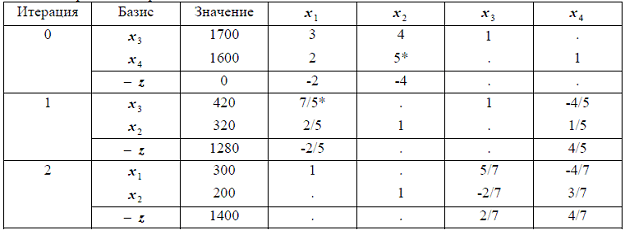
Коэффициенты при x₃ и x₄ в оптимальном виде для функции z равны соответственно 2/7 и 4/7; это и есть симплекс-множители для оптимального базиса.

Ограничения и целевая функция имеют следующий исходный вид:

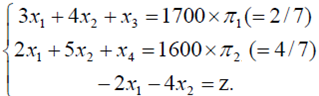
Умножив ограничения (как показано выше) на π₁ и π₂ и прибавив их к функции z, получим

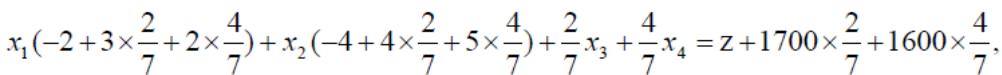
(3.8)

что и является окончательным видом для функции z.

Далее из уравнения (3.5) для функции z в окончательном виде ясно, что коэффициенты при базисных переменных будут нулевыми благодаря выбору π_i, а коэффициенты при небазисных переменных будут положительны. При этом (так как небазисные элементы равны 0) каждое слагаемое в левой части уравнения (3.5) равно 0; либо переменная, либо коэффициент при ней равны 0. Следовательно, оптимальное значение для функции z определяется формулой

т.е. (3.9)

Для только что рассмотренного примера это очевидно (см. уравнение (3.8)).

Во многих задачах множители π_i допускают важную экономическую интерпретацию. Симплекс-множители и обращение оптимального базиса играют важную роль в понимании того, как меняется решение, если слегка изменить условия задачи.