Гипотеза симметричности. Быстрый критерий Кенуя.
Грубый критерий для проверки симметричности в выборках объёма n > 50.
Определяются
порядковые статистики 
,
,
.
По ним вычисляется статистика критерия:
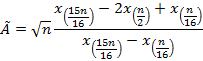
Гипотеза симметрии
отклоняется с достоверностью 
,
если 
(квантиль нормального распределения).
Для
Реализация на Python:
def test_symmetry_Quenouille(massive):
massive = sorted(massive)
n = len(massive)
x1 = massive[n//16]
x2 = massive[n//2]
x3 = massive[(15*n)//16]
result = (n**0.5) * (x3 - 2*x2 + x1) / (x3 - x1)
threshold = 1.96 # квантиль стандартного нормального распределения u0.975
if result > threshold:
return "Гипотеза симметрии распределения отклоняется."
else:
return "Гипотеза симметрии распределения не отклоняется."
Источник литературы для этого метода:
Кенуй М. Г. Упрощенные методы оценивания и проверки //
М.: Статистика, 1979.
Результат выполнения программы на Python:
Анализ глубины просмотра раздела 17.
= = = = = = = = = АНАЛИЗ ВЫБОРКИ MSN-SPORTS (17)= = = = = = = = =
11006 values in range: [1; 81]
mean = 1.542 median = 1.0
variance = 2.894 deviance = 1.701
skewness = 19.058 kurtosis = 738.002
mode = 1 q(3/4) = 2.0
Гистограмма:
1 8081 0.734236
2 1739 0.158005
3 595 0.054061
4 241 0.021897
5 122 0.011085
6 77 0.006996
7 54 0.004906
8 29 0.002635
9 17 0.001545
10 15 0.001363
11 6 0.000545
12 4 0.000363
13 5 0.000454
14 4 0.000363
15 2 0.000182
17 4 0.000363
19 2 0.000182
20 3 0.000273
22 2 0.000182
25 2 0.000182
73 1 0.000091
81 1 0.000091
- - - - - - -
ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ (модифицированный критерий χ^2)
[-170096.46; -0.95] - 0 values
[ -0.95; -0.27] - 0 values
[ -0.27; 0.20] - 0 values
[ 0.20; 0.58] - 0 values
[ 0.58; 0.92] - 0 values
[ 0.92; 1.24] - 8081 values
[ 1.24; 1.54] - 0 values
[ 1.54; 1.85] - 0 values
[ 1.85; 2.16] - 1739 values
[ 2.16; 2.50] - 0 values
[ 2.50; 2.89] - 0 values
[ 2.89; 3.36] - 595 values
[ 3.36; 4.03] - 241 values
[ 4.03; 170099.54] - 350 values
ВЫВОД: 76587.861 > 19.937
Значение критерия больше критического для k = 14 и α = 0.05
Гипотеза нормальности распределения отклоняется.
- - - - - - -
ПРОВЕРКА ЭКСПОНЕНЦИАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ (критерий Колмогорова-Смирнова)
ν = 0.542, μ = 1.000
Dn+ = 0.734, Dn- = 0.108
ВЫВОД: 77.009 > 1.094
Значение критерия больше критического для n -> ∞ и α = 0.05
Гипотеза экспоненциальности распределения отклоняется.
- - - - - - -
ПРОВЕРКА СИММЕТРИИ РАСПРЕДЕЛЕНИЯ (быстрый критерий Кенуя)
Квантили уровня n/16, n/2, 15n/16: 1 - 1 - 3
ВЫВОД: 104.909 > 1.960
Значение критерия больше критического для α = 0.95
Гипотеза симметрии распределения отклоняется.