2. Определение пределов, в которых находится генеральная доля

Нижняя граница 5-го интервала равна 12 (см. 1-ое задание). Доля единиц выборочной совокупности, имеющих значение признака равное или большее 12 равна:

.

Генеральная доля находится в интервале от (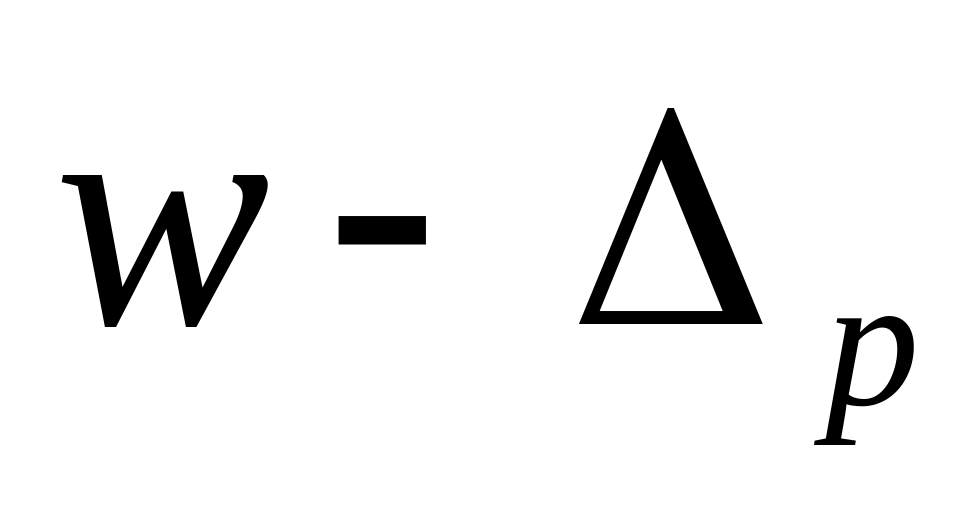 ) до ( ). Где - предельная ошибка доли:

.

Таким образом, генеральная доля с вероятностью 0.997 будет находиться в интервале

от (0.24-0.171) до (0.24+0.171)

или

от 0.067 до 0.411.

3. Определение объема выборки, обеспечивающей заданную точность наблюдения

Объем простой случайной бесповторной выборки определяется по формуле

.

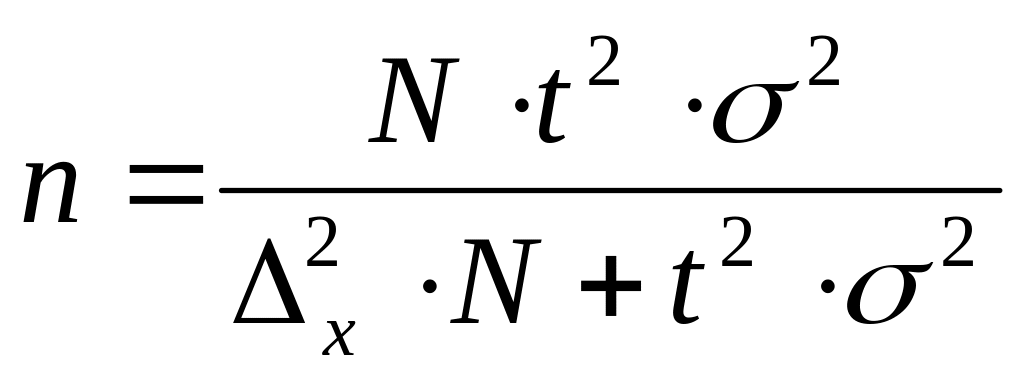По условию задания предельная ошибка выборки .

Поскольку объем выборки - величина целая, то полученное значение необходимо округлить в большую сторону. Таким образом, принимаем размер выборки равный n=84.