Методические указания по выполнению контрольной работы по курсу «Статистика»

I. Задание на контрольную работу:

Задание 1.

На основании исходных данных, выданных преподавателем, необходимо:

1. Построить интервальный ряд распределения, определив величину интервала с помощью формулы Стерджесса.

2. Определить показатели центра распределения.

3. Вычислить показатели вариации.

4. Рассчитать показатели формы распределения.

5. Проверить соответствие эмпирического распределения нормальному закону распределения с помощью критерия согласия Пирсона (или Романовского)

Задание 2.

Считая первые 4 значения первой строки исходных данных уровнями интервального временного ряда, определить показатели динамики. При расчете базисных показателей в качестве базы сравнения принять первый уровень ряда.

Задание 3.

Считая исходные данные 10%-ой простой случайной бесповторной выборкой определить:

1. Пределы, в которых будет находиться генеральное среднее значение признака для всей совокупности с доверительной вероятностью 0.954.

2. Пределы в которых будет находиться генеральная доля единиц совокупности, обладающих значением признака большим или равным нижней границе 5-го интервала, с доверительной вероятностью 0.997.

3. Объем выборки, обеспечивающий получение среднего значения признака с предельной ошибкой не превышающей (σ/5), и вероятностью 0.954.

II. Пример выполнения контрольной работы

Исходные данные:

11	9	2	8	11	5	10	8	4	9
7	6	11	5	18	6	10	7	11	4
12	14	13	8	9	12	5	17	13	17
11	9	1	10	1	5	8	8	0	3
17	3	8	7	4	15	16	3	16	1

Задание 1.

1. Построение интервального вариационного ряда распределения

Ряд распределения – упорядоченное расположение единиц (элементов) изучаемой совокупности по группам в соответствии с выбранным группировочным признаком.

Ряд распределения представляет собой таблицу, которая состоит из двух основных колонок. В первой указываются значения, которые принимает признак в изучаемой совокупности, а во второй – количество, того или иного значения, т.е. частота. Для признака, имеющего непрерывное изменение, строится интервальный ряд распределения. При его построении отдельные значения признака указываются в первой колонке в виде интервалов «от - до».

В некоторых случаях, в зависимости от целей исследования, ряд распределения, состоящий из двух граф, иногда дополняется другими графами, необходимыми для вычисления отдельных статистических показателей.

Для построения интервального ряда вначале определяем размер интервала:

,

где x_max – максимальное значение признака в совокупности;

x_min - минимальное значение признака в совокупности;

m – число интервалов

Количество интервалов определим с помощью формулы Стерджесса:

,

где n – объем совокупности (количество исходных значений). В нашем случае n=50.

Количество интервалов обязательно должно быть целым числом. Поскольку формула Стерджесса дает лишь приблизительную оценку количества интервалов, то можно принять либо m=6, либо m=7. Для удобства дальнейших вычислений примем m=6. Тогда размер интервала будет равен:

.

Следует отметить, что если размер интервала получается дробным, например 2.333…, то его следует округлять обязательно в большую сторону, т.е., например до 2.5.

Определяем границы интервалов. Нижняя граница первого интервала равна минимальному значению признака в совокупности, т.е. в нашем случае равна 0. Верхняя граница первого интервала равна нижней границе плюс размер интервала, т.е. 0+3=3. Нижняя граница второго интервала равна верхней границе первого, т.е. 3. Верхняя граница второго интервала равна нижней границе второго интервала плюс размер интервала, т.е. 3+3=6 и т.д. В итоге получаем границы для шести интервалов. Заносим границы интервалов в таблицу (табл. 1, колонка 2).

Далее подсчитываем количество значений признака из заданной совокупности, попавших в тот или иной интервал и заносим это число в колонку «Частота». Если значение попадает на границу между k-ым и (k+1)-ым интервалами, то его относят в (k+1)-ый интервал. Например, значение признака 9 попадает на границу между 3-м и 4-м интервалами, поэтому его следует относить к 4-му интервалу. Сумма всех частот обязательно должна совпадать с объемом совокупности (в нашем случае со значением 50).

Вычисляем частости, т.е. частоты, выраженные в процентах к общему объему совокупности:

;

;

;

и т. д.

Таблица 1.

Интервальный ряд распределения

№ Инт.	Значение признака (х) от - до	Частота (f)	Частость (w), %	Накопленная частота (S)	Плотность распределения (ρ)
1	0 – 3	5	10	5	1.667
2	3 – 6	10	20	15	3.333
3	6 – 9	11	22	26	3.336
4	9 – 12	12	24	38	4.000
5	12 – 15	5	10	43	1.667
6	15 - 18	7	14	50	2.333
Итого:		50	100	-	-

Накопленная частота показывает сколько единиц изучаемой совокупности имеет значение признака не более чем некоторое заданное. Она вычисляется по формуле:

;

;

и т. д.

Последнее значение накопленной частоты должно быть равно объему совокупности.

Плотность распределения показывает сколько единиц совокупности приходятся на единицу длины интервала:

.

и т.д.

Строим графические изображения ряда распределения.

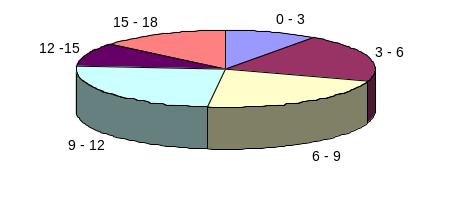
Рис. 1. Структурная диаграмма

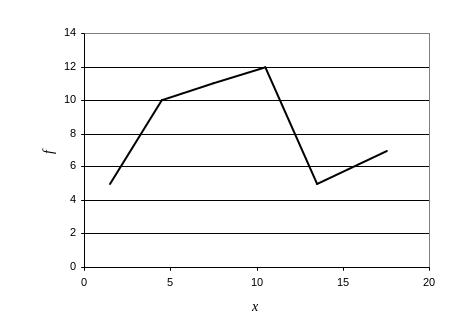
Рис.2. Полигон распределения

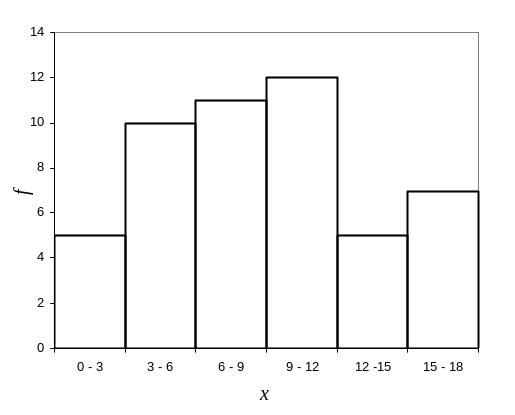
Рис. 3. Гистограмма распределения

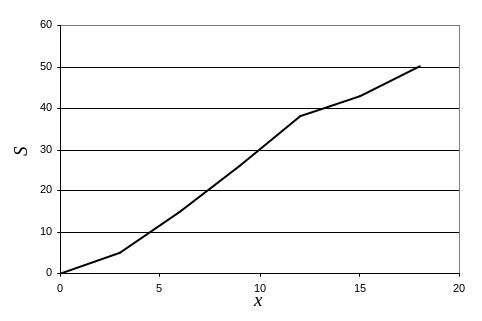
Рис. 4. Кумулятивная кривая