12. Обработка результатов измерений.

1. По данным таблицы 1 на миллиметровой бумаге построить градуировочный график спектрометра. По горизонтальной оси откладываются градусные деления барабана, а по вертикальной – длины волн соответствующих линий.

2. По значениям угла  из таблицы 2 и градуировочному графику определить длины волн линий Н_α, Н_β, Н_.

3. По формуле (4) вычислить экспериментальное значение постоянной Ридберга для каждой из найденных линий и найти её среднее значение.

4. По формуле (3) рассчитать теоретическое значение постоянной Ридберга и сравнить со средним экспериментальным значением.

5. По формуле (1) рассчитать энергии основного и первых трех возбуждённых состояний атома водорода.

6. Исходя из определений, рассчитать энергию ионизации атома водорода и потенциал его ионизации.

13. Контрольные вопросы.

1. Какие закономерности наблюдаются в атомных спектрах?

2. Что такое спектральная серия?

3. Запишите формулу Бальмера и поясните её.

4. Найдите связь постоянной Ридберга с энергией атома водорода в некотором стационарном состоянии.

5. Рассчитайте полную энергию атома водорода, исходя из теории Бора. Какую формулу дает квантовая механика?

6. Изобразите схему уровней энергии атома водорода.

7. Что такое потенциал возбуждения и потенциал ионизации?

8. Как возникают линии Н_α, Н_β, Н_?

9. Как и зачем проводится градуировка спектрометра?

Работа 67. Определение ширины запрещенной зоны полупроводников

1. Цель работы

Экспериментально исследовать зависимость сопротивления полупроводника от температуры, определить ширину запрещенной зоны (энергию активации) и температурный коэффициент сопротивления полупроводника.

14. Приборы и принадлежности:

1. Терморезистор.

2. Электронагреватель.

3. Термометр.

4. Мост сопротивлений.

5. Источник тока.

6. ЛАТР.

7. Соединительные провода.

15. Краткая теория.

Электрон изолированного атома имеет некоторые определенные значения энергии, которые изображают в виде энергетических уровней. На рис.1 представлены энергетические уровни изолированного атома.

Для образования кристалла будем «мысленно» сближать N изолированных атомов. Взаимодействие электрона со всеми N атомами кристалла приводит к изменению энергии электрона. Каждый энергетический уровень атома расщепляется на N уровней, и образуются энергетические зоны (см. рис.2).

В кристалле все энергетические уровни можно разделить на три энергетические зоны. Энергетические уровни валентных электронов атомов образуют валентную зону (см. рис. 3). Свободные электроны могут иметь в кристалле не любые, а дискретные (некоторые определённые) значения энергии. Энергетические уровни свободных электронов образуют свободную зону или зону проводимости.

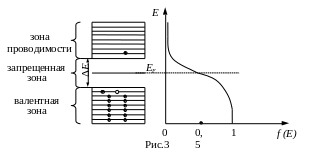
Свободная зона отделена от валентной зоны запрещенной зоной - полосой энергии, запрещенной для электронов. Величина E называется шириной запрещенной зоны.

При температуре электроны кристалла заполняют нижние энергетические уровни. По принципу Паули: на каждом энергетическом уровне может находиться не более двух электронов с противоположно направленными спинами.

У полупроводников при температуре 0 К полностью заполнена электронами валентная зона. В свободной зоне электронов нет. Ширина запрещенной зоны полупроводников небольшая: порядка 1эВ. С ростом температуры электроны, получая энергию, могут переходить на вышележащие энергетические уровни. Энергии теплового движения электронов и энергии электрического поля тока достаточно для перехода электронов из валентной зоны полупроводника в зону проводимости.

При подключении полупроводника к источнику тока в цепи появляется электрическое поле. Свободные электроны в зоне проводимости под действием этого поля движутся противоположно полю (вектору напряженности электрического поля) и образуют электронную проводимость полупроводника. В валентной зоне на месте ушедшего электрона остаётся некомпенсированный положительный электрический заряд – дырка. Под действием электрического поля электрон с соседнего уровня может перейти на место дырки, там, откуда электрон ушел образуется новая дырка. Можно сказать, что дырки движутся по полю. Дырки в валентной зоне образуют дырочную проводимость полупроводника. Электронная и дырочная проводимости химически чистого полупроводника составляют собственную проводимость полупроводника.

Электрическая проводимость в кристалле пропорциональна концентрации носителей тока (электронов и дырок). Распределение электронов по энергетическим уровням характеризуется функцией Ферми - Дирака

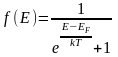, (1)

где Е – энергия электрона, Е_F – энергия Ферми, k = 1,38∙10^-23 Дж/К – постоянная Больцмана, Т – абсолютная температура кристалла.

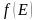– функция Ферми-Дирака, которая определяет вероятность нахождения электрона на энергетическом уровне с энергией Е .

При = 1 на энергетическом уровне находятся 2 электрона;

= 0,5 на энергетическом уровне находится 1 электрон;

= 0 на энергетическом уровне электронов нет.

В металле энергией Ферми называют максимальную кинетическую энергию, которую могут иметь электроны проводимости при температуре 0 К. Энергетический уровень, соответствующий энергии Ферми, называется уровнем Ферми. Таким образом, уровень Ферми – это верхний заполненный электронами энергетический уровень в металле при температуре 0 К.

Значение уровня Ферми в химически чистом полупроводнике, отсчитанное от потолка валентной зоны, приблизительно равно половине ширины запрещенной зоны

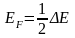. (2)

Отсюда следует что, уровень Ферми находится посередине запрещенной зоны. Если энергия электрона, находящегося в зоне проводимости, равна Е, тогда из рис.3 видно, что

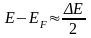(3)

При невысоких температурах в формуле (1) единицей в знаменателе можно пренебречь. Учитывая выражение (3), из формулы (1) получают

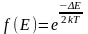. (4)

Удельная проводимость полупроводника 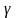пропорциональна концентрации носителей тока, поэтому она пропорциональна функции Ферми – Дирака (формула (4)), тогда можно записать

,

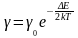где 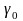– постоянная величина, зависящая от данного полупроводника. Сопротивление обратно пропорционально проводимости, поэтому его можно представить в виде

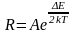, (5)

Здесь А – коэффициент, зависящий от физических свойств полупроводника. Из формулы (5) видно, что с ростом температуры сопротивление полупроводника R уменьшается. По зонной теории эта закономерность объясняется следующим образом: при увеличении температуры растет число электронов в свободной зоне и число дырок в валентной зоне, поэтому проводимость полупроводника увеличивается, а сопротивление уменьшается. У металлов с ростом температуры сопротивление увеличивается.

Для определения ширины запрещенной зоны 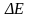необходимо прологарифмировать формулу (5)

(6)

Коэффициент А неизвестен, поэтому сначала записывают формулу (6) для двух разных температур Т₁ и Т₂

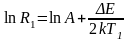, (7)

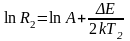. (8)

Вычитают из формулы (7) выражение (8)

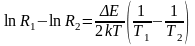. (9)

Из формулы (9) для ширины запрещенной зоны получают расчетную формулу

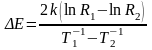(10)

Г рафик зависимости lnR от 1/T для полупроводника с собственной проводимостью представляет собой прямую линию (рис. 4), тангенс угла наклона которой к оси абсцисс равен

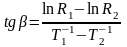. (11)

Сравнивая формулы (10) и (11), можно получить

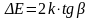
Температурный коэффициент сопротивления 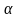показывает относительное изменение сопротивления при нагревании вещества на 1 К

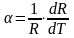. (12)

Единица измерения в СИ .

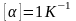Взяв производную сопротивления по температуре в формуле (5), можно записать:

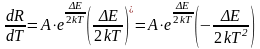(13)

Формулу (13) подставляют в формулу (12) и, учитывая формулу сопротивления R (5), получают

.

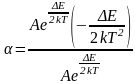Расчетная формула для температурного коэффициента сопротивления полупроводника равна

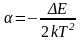. (14)

Температурный коэффициент сопротивления полупроводников зависит от температуры и химической природы вещества. Знак минус в формуле (14) учитывает, что с ростом температуры сопротивление полупроводника уменьшается. У металлов температурный коэффициент сопротивления является положительной величиной.