3 Диагностирование комбинационной логической схемы
3.1 Построение проверяющего теста
Согласно исходных данных, F = {3,4,5,6,7} abc, или F = {011,100,101,110,111}.
В схеме реализуется
функция
Синтезируем схему в полном базисе:
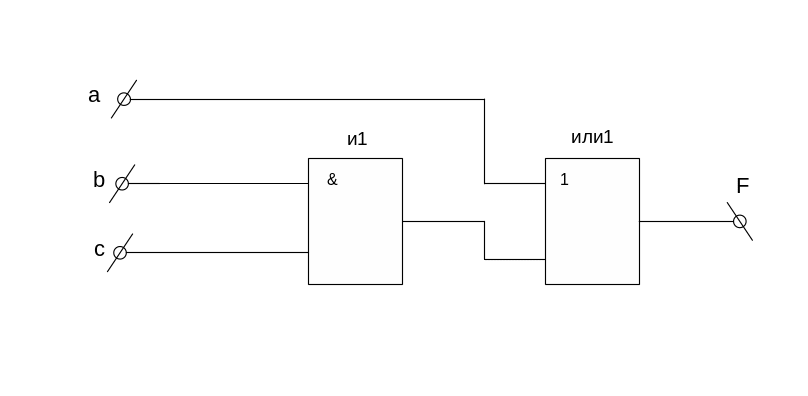
Рисунок 5 – Комбинационная схема, реализующая функцию
Данная схема содержит 6 компонентов и 12 неисправностей
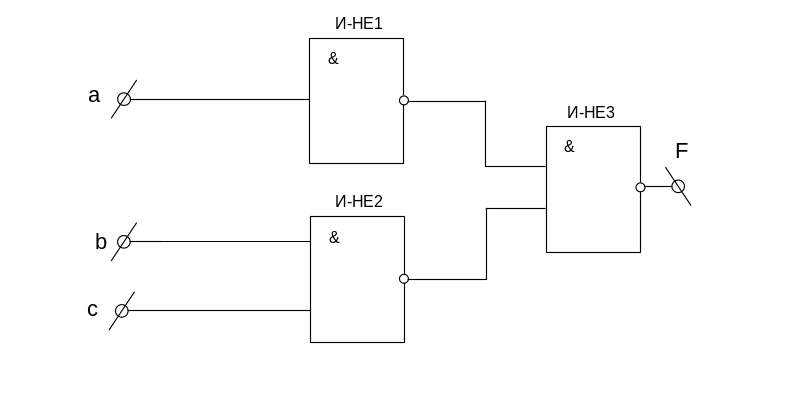
Рис.6 – Комбинационная схема собранная на логических элементах И-НЕ
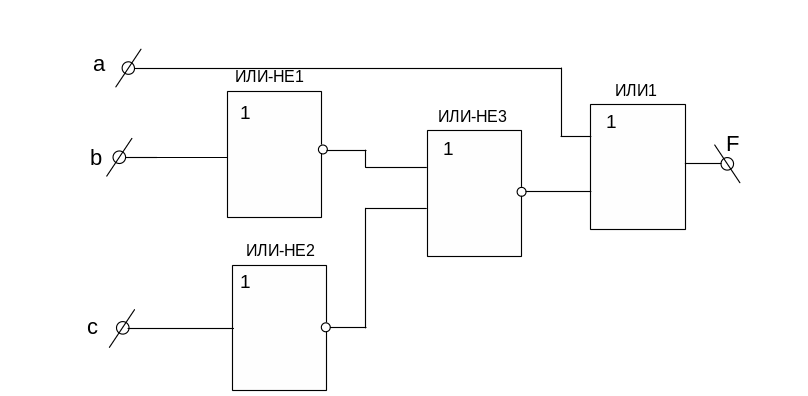
Рис.7 – Комбинационная схема собранная на логических элементах ИЛИ,
ИЛИ-НЕ
Для каждого логического элемента нанесем графы эквивалентных неисправностей и укажем отношения импликации между неисправностями, т.е. установим отношения между неисправностями для всей схемы, и пронумеруем неисправности (рис. 8):
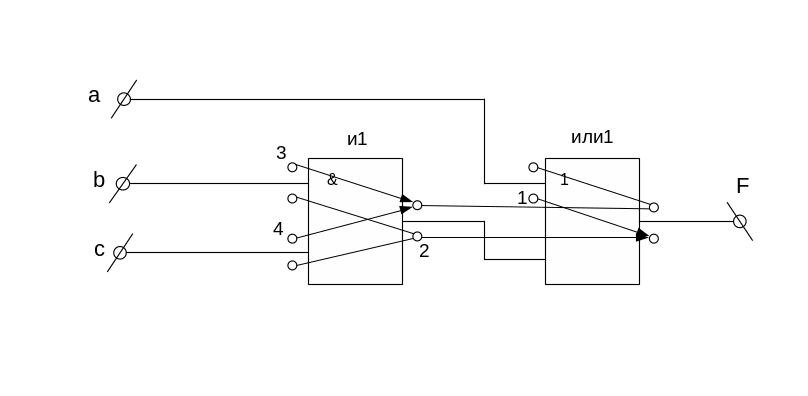
Рисунок 8 – Комбинационная схема с изображением граф эквивалентных неисправностей и указанием отношения
импликации между неисправностями
В результате выполнения данной операции сокращаем список неисправностей с 12 до 4.
Найдем функции неисправностей:
Составим ТФН (таблица 10), в которую включим все пронумерованные неисправности.
Таблица 10 - Таблица функций неисправностей
Вх. набор |
F |
Функция неисправности |
||||
№ |
abc |
f1 |
f2 |
f3 |
f4 |
|
0 |
000 |
0 |
0 |
0 |
0 |
0 |
1 |
001 |
0 |
0 |
0 |
1 |
0 |
2 |
010 |
0 |
0 |
0 |
0 |
1 |
3 |
011 |
1 |
1 |
0 |
1 |
1 |
4 |
100 |
1 |
0 |
1 |
1 |
1 |
5 |
101 |
1 |
0 |
1 |
1 |
1 |
6 |
110 |
1 |
0 |
1 |
1 |
1 |
7 |
111 |
1 |
1 |
1 |
1 |
1 |
Вычислим проверяющие функции в соответствии с выражением (1.1):
φ1 = 4v5v6
φ2 = 3
φ3 = 1
φ4 = 2
В соответствии с выражением (1.2) вычислим проверяющий тест:
Тп = φ1 φ2 φ3 φ4
Тп = (4 v 5 v 6)123= 1234 v 1235 v 1236
Выражение содержит 3 минимальных теста:
Тп1 = 1234,
Тп2 = 1235,
Тп3 = 1236.
3.2 Построение диагностического теста
При построении диагностического теста, не учитывают отношения импликации между неисправностями. На схему наносят только графы эквивалентных неисправностей, которые нумеруются (рис.9). В результате число неисправностей, включаемых в ТФН, увеличивается. По диагностическому тесту строят словарь неисправностей.
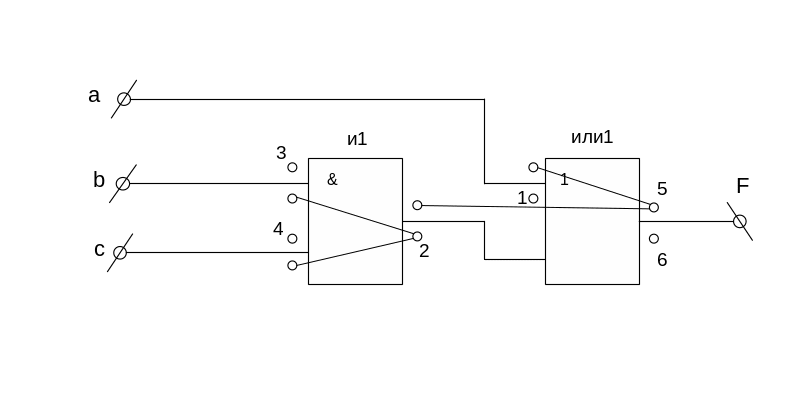
Рисунок 9 – Эквивалентные неисправности
комбинационной схемы
Составим ТФН. Таблица будет аналогична таблице 10, но в неё необходимо включить две неисправности выхода системы, которым соответствуют функции неисправностей f5 = 1 и f6 = 0.
Таблица 11 - Таблица функций неисправностей
Вх. набор |
F |
Функция неисправности |
|||||||
№ |
abc |
f1 |
f2 |
f3 |
f4 |
F5 |
F6 |
|
|
0 |
000 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
001 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
2 |
010 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
3 |
011 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
4 |
100 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
5 |
101 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
6 |
110 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
7 |
111 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
Проверяющие функции для f9 и f10 :
φ5 = 0 v 1 v 2
φ6 = 3 v 4 v 5 v 6 v 7
Определим различающие функции в соответствии с выражением (1.3):
φ1,2= 3 v 4 v 5 v 6
φ1,3= 1 v 4 v 5 v 6
φ1,4= 2 v 4 v 5 v 6
φ1,5= 0 v 1 v 2 v 4 v 5 v 6
φ1,6= 3 v 7
φ2,3 = 1 v 3
φ2,4 = 2 v 3
φ2,5 = 0 v 1 v 2 v 3
φ2,6 = 4 v 5 v 6 v 7
φ3,4 = 1 v 2
φ3,5 = 0 v 2
φ3,6 = 1 v 3 v 4 v 5 v 6 v 7
φ4,5 = 0 v 1
φ4,6 = 2 v 3 v 4 v 5 v 6 v 7
φ5,6 = 0 v 1 v 2 v 3 v 4 v 5 v 6 v 7
Если составить диагностический тест, согласно выражению (1.4), то, подставив значения функций и упростив выражение, получим:
Тд= (3 v 4 v 5 v 6)(1 v 4 v 5 v 6)(2 v 4 v 5 v 6)(4 v 5 v 6 v 7)(3 v 7)(1 v 3)(2 v 3) (1 v 2)(0 v 2)(0 v 1)
Tд=0234 v 0134 v 0235 v 0135 v 0236 v 0136 v 01234 v 1234 v 1235 v 1236 v 01247 v 01347 v 01257 v 01357 v 01267 v 01367 v 012347 v 1247 v 1257 v 1267 v 12347
Полученное выражение содержит 12 минимальных тестов:
Тд1 = 0234
Тд2 = 0134
Тд3 = 0235
Тд4 = 0135
Тд5 = 0236
Тд6 = 0136
Тд7 = 1234
Тд8 = 1235
Тд9 = 1236
Тд10 = 1247
Тд11 = 1257
Тд12 = 1267
Диагностический тест Тд’, согласно выражению (1.5) равен:
Тд’= Тп φ1,2 φ1,3,……,φn-1,n .
Подставив значения функций и упростив выражение, получим:
Тд’= (0234 v 0134 v 0235 v 0135 v 0236 v 0136 v 01234 v 1234 v 1235 v 1236 v 01247 v 01347 v 01257 v 01357 v 01267 v 01367 v 012347 v 1247 v 1257 v 1267 v 12347)(1234 v 1235 v 1236) = 1234 v 1235 v 1236
Тд’1 = 1234
Тд’2 = 1235
Тд’3 = 1236
Составим словарь неисправностей для теста Тд’1 = 1234 (таблица 12):
Таблица 12 - Словарь неисправностей для Тд’1
Вх. набор |
F |
Функция неисправности |
||||||
№ |
abc |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
|
1 |
001 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
2 |
010 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
3 |
011 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
4 |
100 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
Составим словарь неисправностей для теста Тд’2 = 1235 (таблица 13):
Таблица 13 - Словарь неисправностей для Тд’2
Вх. набор |
F |
Функция неисправности |
||||||
№ |
abc |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
|
1 |
001 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
2 |
010 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
3 |
011 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
5 |
101 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
Составим словарь неисправностей для теста Тд’3 = 1236 (таблица 14):
Таблица 14 - Словарь неисправностей для Тд’3
Вх. набор |
F |
Функция неисправности |
||||||
№ |
abc |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
|
1 |
001 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
2 |
010 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
3 |
011 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
6 |
110 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |