2 Построение тестов для комбинационной релейно-контактной схемы

2.1 Построение проверяющего теста

Рассмотрим построение тестов для комбинационной релейно-контактной схемы, заданной в виде ФАЛ.

F = {0,1,2,4,6} a,b,c.

F = {000,001,010,100,110}

Минимизируем данную ФАЛ с помощью карты Карно:

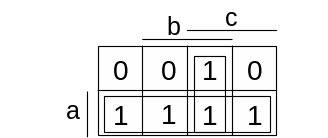
Рисунок 2 – Карта Карно функции F

В результате получаем минимизированную функцию:

Комбинационная релейно-контактная схема, соответствующая полученной ФАЛ приведена на рис. 3:

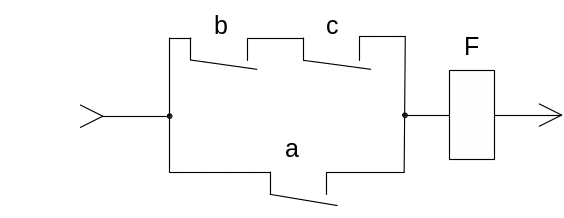
Рисунок 3 – Комбинационная релейно-контактная схема

Элементарная проверка для схемы заключается в подаче на ее входы определенного набора значений входных переменных и определении факта наличия проводимости схемы по состоянию реле F.

Определим функции неисправностей:

Составим ТФН (таблица 5):

Таблица 5 - Таблица функций неисправностей

Вх. набор		F	f1	f2	f3	f4	f5		f6
			При внесении неисправности
№	abc		a1	a0	b1	b0	c1	c0
0	000	0	1	0	0	0	0		0
1	001	0	1	0	1	0	0		0
2	010	0	1	0	0	0	1		0
3	011	1	1	1	1	0	1		0
4	100	1	1	0	1	1	1		1
5	101	1	1	0	1	1	1		1
6	110	1	1	0	1	1	1		1
7	111	1	1	1	1	1	1		1

Определим проверяющие функции:

Φ₁= 0 v 1 v 2

φ₂= 4 v 5 v 6

φ₃= 1

φ₄= 3

φ₅= 2

Проверяющий тест, в соответствии с выражением (1.2) равен:

Т_п = φ₁φ₂φ₃φ₄φ₅

Т_п = (0 v 1 v 2)(4 v 5 v 6)123, раскрыв скобки, получим:

Т_п = 1234 v 1235 v 1236.

Данный проверяющий тест содержит 3 минимальных теста:

Т_п1 = 1234;

Т_п2 = 1235;

Т_п3 = 1236.

2.2. Построение диагностического теста.

Для построения диагностического теста определим различающие функции, согласно выражению (1.3):

φ_1,2 = 0 v 1 v 2 v 4 v 5 v 6

φ_1,3 = 0 v 2

φ_1,4 = 0 v 1 v 2 v 3

φ_1,5 = 0 v 1

φ_2,3 = 1 v 4 v 5 v 6

φ_2,4 = 3 v 4 v 5 v 6

φ_2,5 = 2 v 4 v 5 v 6

φ_3,4 = 1 v 3

φ_3,5 = 1 v 2

φ_4,5 = 2 v 3

Диагностический тест строится согласно выражению (1.4). Для данного случая имеет вид:

Т_д = (0 v 1 v 2 v 4 v 5 v 6)( 0 v 2)( 0 v 1 v 2 v 3)( 0 v 1)( 1 v 4 v 5 v 6)( 3 v 4 v 5 v 6)( 2 v 4 v 5 v 6)( 1 v 3)( 1 v 2)( 2 v 3) = 124 v 0134 v 0234 v 125 v 0135 v 0235 v 126 v 0136 v 0236 v 123 v 0123

Выражение содержит 4 минимальных теста:

Т_д1 = 123

Т_д2 = 124

Т_д3 = 125

Т_д4 = 126

Воспользовавшись выражением (1.5), определим Т_д^’ :

Т_д^’ = (1234 v 1235 v 1236)(123v124v125v126)

Упростив выражение, получим:

Т_д^’= 1234v12345v12346v1235v12356v1236

Это выражение содержит 3 минимальных теста:

Т_д1^’= 1234

Т_д2^’= 1235

Т_д3^’= 1236

Из Т_д и Т_д^’ выбираем Т_д и составляем словари неисправностей для тестов

Т_д1 - Т_д4.

_{Таблица 6 - Словарь неисправностей для Тд1}

Вх. набор		F	f1	f2	f3	f4	f5		f6
			При внесении неисправности
№	abc		a1	a0	b1	b0	c1	c0
1	001	0	1	0	1	0	0		0
2	010	0	1	0	0	0	1		0
3	011	1	1	1	1	0	1		0

_{Таблица 7 - Словарь неисправностей для Тд2}

Вх. набор		F	f1	f2	f3	f4	f5		f6
			При внесении неисправности
№	abc		a1	a0	b1	b0	c1	c0
1	001	0	1	0	1	0	0		0
2	010	0	1	0	0	0	1		0
4	100	1	1	0	1	1	1		1

_{Таблица 8 - Словарь неисправностей для Тд3}

Вх. набор		F	f1	f2	f3	f4	f5		f6
			При внесении неисправности
№	abc		a1	a0	b1	b0	c1	c0
1	001	0	1	0	1	0	0		0
2	010	0	1	0	0	0	1		0
5	101	1	1	0	1	1	1		1

_{Таблица 9 - Словарь неисправностей для Тд}4

Вх. набор		F	f1	f2	f3	f4	f5		f6
			При внесении неисправности
№	abc		a1	a0	b1	b0	c1	c0
1	001	0	1	0	1	0	0		0
2	010	0	1	0	0	0	1		0
6	110	1	1	0	1	1	1		1

В таблице мы выделили классы эквивалентных неисправностей. Поиск неисправности осуществляют таким образом. На входы схемы последовательно подаются входные наборы, входящие в диагностический тест. Для каждого случая фиксируются значения выхода схемы (например, по состоянию реле F). Полученные результаты сравнивают с данными, приведенными в табл.. Если значения совпадают, то схема исправна. В противном случае полученные значения состояния реле F указывают на класс эквивалентных неисправностей, внутри которого находится неисправность, имеющаяся в схеме. Точное указание неисправности внутри класса эквивалентных неисправностей возможно только при измерениях во внутренних точках схемы.