3.6. Статистическое (эффективное) кодирование.

С одной стороны, большая избыточность сообщений затрудняет информационный обмен, требуя излишних затрат энергии и времени на передачу сообщений. С другой стороны, сооб­щения, обладающие малой информационной избыточностью, оказываются весьма чувствитель­ными к действию помех, а это, в свою очередь, затрудняет обеспечение достоверности их пере­дачи по реальным каналам телекоммуникационных систем.

Именно поэтому все информационные преобразования сообщений и сигналов разделяются на два основных класса: одни имеют целью уменьшить первичную (естественную) избыточ­ность сообщений, чтобы повысить эффективность их передачи, другие направлены на то, чтобы внести дополнительную (искусственную) избыточность для повышения достоверности (поме­хоустойчивости) передаваемых сообщений.

Если в результате кодирования избыточность сообщений уменьшается – такое кодирова­ние называется эффективным (иначе – кодированием для источника), если избыточность воз­растает, кодирование называется помехоустойчивым (иначе – кодирование для канала). Если в результате кодирования избыточность сообщений сохраняется без изменений, то кодирование называется примитивным.

При наличии избыточности кодовой последовательности , символы a_i которой должны быть закодированы таким образом, чтобы избыточность кодовой последовательности была как можно меньше. Коды, обеспечивающие такое преобразование, при котором называются статистиче­скими или эффективными.

Избыточность дискретного источника характеризует степень использования информационной емкости алфавита источника: если , емкость алфавита используется пол­ностью, если , то, в принципе

существует иной, более сжатый способ представления сооб­щений источника. Т. е., можно трактовать как относительную долю букв, необязательных для понимания смысла сообщений.

Производительность источника сообщений определяется количеством передаваемой информации за единицу времени. С понятием количества информации связано понятие функции неожиданности , где - вероятность появления сообщения . Таким образом, чем больше неожиданность отдельного сообщения (меньше вероятность его появления), тем больше оно информативно. Количество информации – есть логарифмическая функция от функции неожиданности . Количество информации, передаваемое символом, вероятность появления которого , то есть , называют битом.

Среднее значение информации, передаваемое одним символом, называют энтропией (рассеянием) информации. Энтропия определяется как математическое ожидание от всего ансамбля сообщений:

, где N – алфавит сообщения.

Максимальное значение энтропии достигается при равенстве вероятностей всех символов сообщения, причём эти вероятности должны определяться как , так для дискретного источника двоичных сообщений максимальное значение энтропии:

^бит/_символ.

Найдём энтропию источника в нашем случае. По заданию вероятность передачи символа "1" - , тогда

, Бит.

По полученному значению энтропии определим производительность источника до применения статистического кодирования:

Бит/с кБит/с (кБод). (2.6.1)

Найдём информационную избыточность сообщения:

. (2.6.2)

Полученное значение , следовательно, требуется применение статистического уплотнения, так как это даёт значительное изменений избыточности.

Конструктивные методы построения эффективных кодов были даны впервые американскими учеными Шенноном и Фано. Их методики существенно не различаются, и поэтому соответствующий код получил название Шеннона – Фано.

Код строят следующим образом: знаки алфавита сообщений выписывают в таблицу в порядке убывания вероятности. Затем их разделяют на две группы так, чтобы суммы вероятностей каждой из групп были по возможности одинаковы. Всем знакам верхней половины, в качестве первого символа приписывают 0, а всем нижним -1. Каждую из полученных групп, в свою очередь, разбивают на две подгруппы с одинаковыми суммарными вероятностями и т.д. Процесс повторяется до тех пор, пока в каждой подгруппе не останется по одному знаку. Важным свойством кода Шеннона - Фано является то, что несмотря на его неравномерность, здесь не требуется разделительных знаков. Это обусловлено тем, что короткие комбинации не являются началом наиболее длинных комбинаций.

Основной принцип оптимального кодирования сводится к тому, что наиболее вероятным сообщениям должны присваиваться короткие комбинации, а сообщениям с малой вероятностью - более длинные комбинации. Рассмотренная методика Шеннона - Фано не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы можно сделать большей по вероятности, как одну, так и другую подгруппы.

От указанного недостатка свободна методика Хаффмена. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.

Осуществим статистическое уплотнение методом Хаффмена для трёхсимвольных комбинаций двоичного кода. При равномерном блочном коде каждый символ Z_i представляется символами кодовой комбинации. Таких комбинаций будет . Найдём вероятности этих комбинаций:

p(000)=0.15*0.15*0.15=0.003375

p(001)=p(010)=p(100)=0.15*0.15*0.85=0.019125

p(011)=p(101)=p(110)=0.15*0.85*0.85=0.108375

p(111)=0.85*0.85*0.85=0.614125

Для выбора кодовых ком­бинаций при статистическом кодировании символы сообщений располагаются в порядке убы­вания их вероятностей (таблица 2.6.1). Далее два наименее вероятных элемента объединяются в один, и тем же способом (в порядке убывания вероятностей) выписывается вспомогательный ан­самбль, состоящий из исходных и одного объединенного элемента (вероятность послед­него равна сумме вероятностей объединяемых).

Затем вспомогательный ансамбль подвергается аналогичному преобразованию и т.д. до получения ансамбля из одного элемента, имеющего вероятность P(a₁) +  P(a₂) + … + P(a₈) = 1.

По данным полученной таблице строим кодовое дерево следующим образом. Из точки с вероятностью "1" направляем две ветви. Ветви с большей вероятностью приписываем 1 и откладываем влево, а ветви с меньшей вероятностью приписываем 0 и откладываем вправо. Такое последовательное ветвление продолжим до тех пор, пока не дойдем до вероятности каждой отдельной буквы. Теперь новые кодовые комбинации можно найти по графу (рисунок 2.5.1), отображающему описанные операции. Так, для приведенного примера:

, , , , , ,

(перемещение по графу (кодовому дереву) влево соответствует символу 1, перемещение вправо – символу 0).

Для повышения эффективности передачи дискретных сообщений наряду с рассмотренными методами применяют также разнесенный прием сигналов, прием в целом, системы с информационной и решающей обратной связью, системы с шумоподобными сигналами и другие. Успешно разрабатываются методы повышения эффективности непрерывных, в частности, речевых и телевизионных сигналов на основе принципов сокращения избыточности.

Найдём производительность источника после применения статистического кодирования:

Определим среднюю длину кодового слова по формуле:

, где 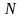– объём алфавита источника, - длина -го элемента, - вероятность -го элемента.

Тогда для полученного кода средняя длина комбинаций будет равна:

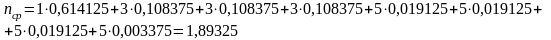
Так как полученные комбинации фактически содержат информацию о трёх элементарных сигналах, то, исходя из этого, средняя длина новых комбинаций в расчете на одну букву первоначального двоичного кода составляет третью часть от полученного значения, поэтому:

Рассчитаем значение энтропии источника после применения статистического кодирования:

Тогда производительность источника будет равна:

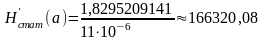, Бит/с (Бод) = 166,32 кБит/с (кБод) (2.6.3)

Полученное значение говорит о том, что благодаря применению статистического кодирования производительность источника увеличивается почти в три раза.

Таблица 3.6.1

Знаки	Вероятности	Вспомогательные дополнительные столбцы
		1	2	3	4	5	6	7
z1	0.614	0.614	0.614	0.614	0.614	0.614	0 .614	1
z2	0.108	0.108	0.108	0.108	0 .168	0 .216	0 .384
z3	0.108	0.108	0.108	0 .108	0.108	0.168
z4	0.108	0.108	0.108	0.108	0.108
z5	0 .019	0 .022	0 .038	0 .06
z6	0 .019	0.019	0.022
z7	0.019	0.019
z8	0.003