3.4. Сравнение выбранной схемы с оптимальным приемником Котельникова.
Оптимальный приемник – это когерентный приемник, в котором применяется интегратор (в приемнике Котельникова оптимальный фильтр), а принятие решения приемником производится в конце каждой элементарной посылки.
Оптимальный
приемник работает следующим образом:
определяется среднеквадратичное
отклонение поступившего на его вход
сигнала Z(t)
от обоих ожидаемых сигналов
и
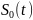и выносится решение в пользу того
сигнала, где это среднеквадратичное
отклонение меньше.
Если
при вычислении условных вероятностей
расстояние между сечениями
устремить к нулю, т.е. сделать
меньше интеграла корреляции помехи,
работа приемника не улучшается, так как
соседние сечения будут сильно
коррелированы, но и не ухудшится. Поэтому
в правиле решения можно заменить
суммирование интегрированием.
В соответствие с полученным правилом решения структурная схема приемника будет иметь вид:
Рисунок 3.4.1 Структурная схема оптимального приемника.
Схема
содержит два генератора опорных сигналов
и
,
которые генерируют точно такие же
сигналы, которые могут поступить на
вход приемника, а так же два вычитающих
устройства, два квадратора, два интегратора
и схему сравнения, которая выдает сигналы
и
.
Помехоустойчивость приемника достигается благодаря тому, что при приеме учитываются все параметры сигнала, не несущие информации: амплитуда, частота, фаза несущего колебания, а так же длительность сигнала Т, так как интегрирование осуществляется в течение этого времени.
– формула
в общем виде, где
– интеграл
вероятности.
– коэффициент
взаимной корреляции между двоичными
сигналами;
Е – энергия сигнала;
– спектральная плотность мощности помехи.
Энергия
сигнала Е
определяется известными параметрами
сигнала:
– мощностью сигнала и Т
– длительностью сигнала (длительностью
элементарной посылки) и в общем виде
равно:
Для разных видов модуляции потенциальная помехоустойчивость различна.
Дискретная амплитудная модуляция.
При
Алгоритм различия сигналов принимает вид:
Плотность
вероятности w(q|
)
и w(q|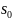
)
описываются гауссовским законом с
параметрами
и
соответственно.
При
средняя вероятность ошибки:
Учитывая,
что порог
,
находим
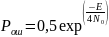и
;
Дискретная частотная модуляция.
При
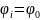коэффициент взаимной корреляции между
этими сигналами:
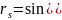
Минимальное
значение коэффициента взаимной корреляции
между частотно-модулированными сигналами
равно
.
Оно достигается, когда
Вероятность
ошибки при этом:
.
Дискретная фазовая модуляция.
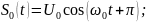
При
Для
этих сигналов
Меньшей
помехоустойчивостью обладают ортогональные
сигналы, например, фазоманипулированные
с манипуляцией фазы
:
Для
них вероятность ошибки:
Сравнивая
между собой формулы вероятности ошибки,
видим, что для достижения заданной
вероятности ошибки при ДЧМ требуется
величина
в
раза больше, чем при ДФМ, а при ДАМ – в
2 раза больше, чем при ДФМ. Отсюда видно,
что переход от ДАМ к ДЧМ дает двукратный
выигрыш по мощности, а к ДФМ – четырехкратный
выигрыш. Причину этого можно установить,
рассматривая векторные диаграммы
сигналов для разных видов модуляции.
Рисунок 3.4.2 Векторные диаграммы ДАМ, ДЧМ, ДФМ.
Из
рис. 3.4.2 видно, что при ДАМ расстояние
между векторами сигналов
и
равно длине вектора
,
при ДЧМ (взаимно ортогональные сигналы)
это расстояние равно
при ДФМ (противоположные сигналы) это
расстояние равно
Энергия же пропорциональна квадрату
разности сигналов.
Следует заметить, что приведенные здесь данные об энергетике сигналов ДАМ, ДЧМ относились к максимальным (пиковым) мощностям этих сигналов. В этом смысле, например, при переходе от ДЧМ к ДАМ мы имеем двукратный выигрыш в пиковой мощности.
Однако, сигналы ДАМ имеют пассивную паузу (мощность сигнала в паузе равна нулю), поэтому по потребляемой передатчиком мощности, кроме отмеченного ранее проигрыша, имеется еще и двукратный выигрыш. С учетом этого обстоятельства, при переходе от ДЧМ к ДФМ двукратный проигрыш по пиковой мощности компенсируется двукратным выигрышем за счет пассивной паузы сигналов ДАМ, в результате чего по потребляемой мощности эти сигналы оказываются равноценными. Однако следует помнить, что при ДАМ в приемнике Котельникова трудно установить необходимый порог в сравнивающем устройстве, а в приемнике ДЧМ регулировка порога не требуется. Поэтому частотная модуляция применяется чаще, чем амплитудная.
Вычислим
отношение энергии сигнала к спектральной
мощности помехи и определим вероятность
ошибки при использовании оптимального
приемника Котельникова.
Оптимальный приемник известных сигналов с пассивной паузой.
Пусть
сигналы
(дискретная амплитудная модуляция).
Подставим
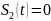в неравенство
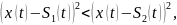получим
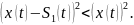Это преобразуется в
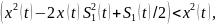сократив
получим
или окончательно,
то
– это оптимальное правило решения приемника для известных сигналов с пассивной паузой;
– функция
взаимной корреляции сигнала на входе
приемника x(t)
и ожидаемого сигнала
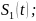
– мощность
сигнала
на входе приемника.
В
соответствии с правилом (*) структурная
схема приемника примет вид (рис. ). Здесь
производится перемножение входного
сигнала x(t)
на опорное 
напряжение
местного генератора сигналов
(в данном случае
).
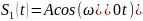Приведенная схема называется корреляционным
приемником, так как вычисляется функция
взаимной корреляции входного сигнала
x(t)
и местного сигнала
,
а в схеме сравнения функция корреляции
сравнивается с некоторым порогом
,
значение которого равно
(когда
то значение порога становится равным
Правило
решения (*) имеет простой физический
смысл. Если функция взаимной корреляции
сигнала x(t)
и сигнала
достаточно велика, значит x(t)
кроме помехи содержит также сигнал
и приемник выдает сигнал
.
Если же эта функция взаимной корреляции
достаточно мала, значит x(t)
не содержит сигнала
,
т.е. x(t)
содержит только одну помеху. В этом
случае приемник выдает сигнал
Приемник Котельникова обеспечивает наибольшую потенциальную помехоустойчивость. Это достигается благодаря тому, что при приеме учитываются все параметры сигнала, не несущие информации: амплитуда, частота, фаза несущего колебания, а также длительность сигнала T, так как интегрирование (фильтрация) осуществляется в течении этого времени.
Потенциальною помехоустойчивость можно получить с помощью любого когерентного приемника при условии использования его в схеме оптимального фильтра, обеспечивающего оптимальную фильтрацию.
Оптимальный
приемник является корреляционным,
сигнал на его выходе представляет собой
функцию корреляции принимаемого сигнала
x(t)
и ожидаемого
благодаря чему обеспечивается максимально
– возможное отношение сигнал/шум
Поскольку
операция определения функции корреляции
является линейной, ее можно реализовать
в некотором линейном фильтре, 
характеристики
которого (комплексная передаточная
характеристика K(jω)
и импульсная характеристика g(t))
являются такими, что отношение сигнал/шум
на его выходе получается максимальным,
причем
Передаточная характеристика в комплексной форме имеет вид:
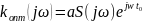
S*(jω) – комплексно-сопряженный спектр по отношению к S(jw)
Отношение сигнал/помеха определяется формулой:
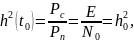где
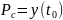– мощность
сигнала на выходе фильтра в момент
;
– мощность
помехи на выходе фильтра;
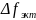– эффективная
полоса пропускания оптимального фильтра;
E – энергия сигнала S(t) на входе фильтра.
Отношение
численно равно отношению энергии сигнала
к спектральной плотности помехи (как в
приемнике Котельникова) и не зависит
от формы сигнала. А так как энергия
сигнала равна произведению мощности
сигнала на его длительность, то для
повышения помехоустойчивости систем
связи с использованием согласованных
фильтров можно увеличить длительность
элементарных сигналов.
Импульсная
характеристика оптимального фильтра
определяется выражением
Таким
образом, функция g(t)
отличается от сигнала S(t)
только постоянным множителем
,
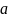смещением на величину
и знаком аргумента t
(то
есть функция g(t)
является зеркальным отображением
сигнала S(t),
сдвинутым на величину
).
Величину
обычно берут равной длительности сигнала
T.
Если взять
,
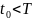то получается неосуществимая система
(отклик начинается раньше поступления
входного воздействия).
На выходе согласованного фильтра получаем под действием сигнала функцию корреляции сигнала, а под действием помехи функцию взаимной корреляции сигнала и помехи. Если на входе фильтра только помеха, на выходе получаем только функцию взаимной корреляции помехи и сигнала, которым фильтр согласован.
Рассмотрим оптимальный фильтр, согласованный с прямоугольным импульсом длительности Т.
Спектральная плотность прямоугольного импульса равна:
Для
согласованного фильтра
.
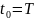Пользуясь
последним выражением, построим схему
фильтра для данного случая. Так из теории
электрических цепей известно, что
деление на
означает интегрирование сигнала,
множитель
означает задержку сигнала на время Т.
В результате, схема фильтра будет
содержать интегратор, линию задержки
и вы читатель (рисунок 3. 4.3).
Рисунок 3.4.3 структурная схема фильтра.
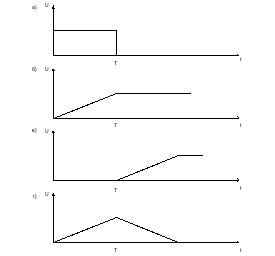
Рисунок 3.4.4 Диаграмма состояний согласованного фильтра.
Таким образом, на выходе фильтра получился треугольный импульс с основанием 2T (это функция корреляции входного импульса прямоугольной формы). То, что выходной импульс имеет в два раза большую длительность, чем входной является недостатком оптимального фильтра, так как «хвост» выходного сигнала на отрезке времени от Т до 2Т будет накладываться на выходной сигнал следующего импульса, что является недостатком оптимального фильтра, называемым межсимвольной интерференцией.
Поэтому на практике часто применяют упрощенную схему фильтра, содержащую интегрирующую RC-цепь (RC >>T) и ключ К. В момент Т окончания входного импульса. Фильтры с ключами называются кинематическими фильтрами.
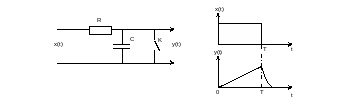
Рисунок
3.4.5 схема кинематического фильтра.