23. Энергетические уровни водородоподобных атомов

Атом водорода, также ионизированный атом гелия( кот-го еще наз-ют водородоподобным атомом), явл-ся простейшими атомными системами. Потенц-ая энергия водородоподобного атома равна:

U(r)=- Ze²/r, поэтому Ур-ие Шредингера для нахождения состояний электрона в таком атоме имеет след вид:

(-ħ²/2m)∆ψ- (Ze²/r)ψ= Eψ

Оператор Лапласа выражают ∆=d²/dr² + 2d/rdr. Тогда Ур-ие Шредин-ра имеет вид:

-ħ²/2m (d²ψ/dr² + 2dψ/rdr ) – (Ze²/r)ψ = Eψ. Из этого Ур-ия можно получить возможные собс-ые значения оператора энергии: E= (-Z²R1)/ n². Из выражения следует что энергии электрона в водородоподобном атоме как и у частицы в потенц-ой яме также явл-ся дискретными.

№24. Линейный гармонический осциллятор – система, совершающая одномерное движение под действием квазиупругой силы, является моделью, которая часто используется при описании классических и квантовых систем. Пружинный, физический и математический маятники – примеры классических гармонических осцилляторов. Потенциальная энергия гармонического осциллятора равна: U=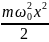 , где

- собственная частота колебаний осциллятора. m – масса частицы.

Гармонический осциллятор в квантовой механике – квантовый осциллятор – описывается уравнением Шредингера вида + , где

E - полная энергия осциллятора. Рис4

Собственные значения энергии для этого уравнения: 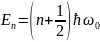(n=0,1,2,…)

Таким образом, энергия квантового осциллятора квантуется (может иметь лишь дискретные значения). Уровни энергии расположены на одинаковых расстояниях, равных . Минимальная энергия называется энергией нулевых колебаний. Существование энергии нулевых колебаний – типично квантовый эффект – прямое следствие соотношение неопределенностей. Частица в яме любой формы не может находиться на ее дне, поскольку в нуль обращается импульс частицы и его неопределенность, а неопределенность координаты становится бесконечной, что противоречит, в свою очередь, условию пребывания частицы в “потенциальной яме “.

Правилами отбора в квантовой механике называются условия, накладываемые на изменения квантовых чисел.

Для гармонического осциллятора возможны лишь переходы между соседними подуровнями, т.е. переходы, удовлетворяющие правилу отбора: . Следовательно, энергия гармонического осциллятора может изменяться только порциями и гармонический осциллятор испускает и поглощает энергию квантами.

Квантово-механическое решение задачи о квантовом осцилляторе показывает, что имеется отличная от нуля вероятность, обнаружить частицу за пределами области 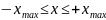. Cуществование отличных от нуля значений вероятности обнаружения частицы за пределами потенциальной ямы объясняется возможностью прохождения микрочастиц сквозь потенциальный барьер.

На рис 5 приведена квантовая плотность вероятности обнаружения осциллятора при , имеющая конечные значения для .

№25 Связь между квантовыми числами. Изучение атомных орбиталей, рассчитанных с помощью уравнения Шредингера, показало, что характер движения электрона в атоме определяется четырьмя числами - п, l, m, s, получившими общее название квантовых чисел: главное, орбитальное, магнитное и спиновое.

Главное квантовое число n. Это число может принимать любые положительные целочисленные значения: n = 1, 2, 3. Определяет орбитальный радиус и соответствующий главный энергетический уровень E_n. Совокупность атомных орбиталей с одинаковым значением главного квантового числа n составляют одну электронную оболочку.

Орбитальным радиусом r_орб называют расстояние от ядра атома до наиболее удаленной точки поверхности, изображающей атомную орбиталь. Для сферической поверхности орбитальный радиус равен радиусу сферы. Для поверхности в виде песочных часов орбитальный радиус равен диаметру одной из составляющих сфер (рис. 3.1).

Главным энергетическим уровнем называют часть энергии атома, определяемой главным квантовым числом п.

Рис. 3.1. Определение орбитального радиуса r_орб для атомных орбиталей разной формы: а - s-орбитали; б - _р-орбитали

Энергия притяжения между электроном и ядром уменьшается обратно пропорционально квадрату главного квантового числа n², а орбитальный радиус r_орб увеличивается пропорционально этой величине. С увеличением числа п электрон в среднем находится все дальше от ядра. При п → ∞ энергия притяжения становится равной нулю, электрон отрывается от ядра. Происходит ионизация атома.

Таким образом, главные энергетические уровни Е_п атома можно определять экспериментально измерением минимальной энергии, необходимой для отрыва электрона от атома. Определяемая таким способом величина называется энергией ионизации атома - I. Это очень важная характеристика атома, от которой зависят его свойства, в частностиэлектроотрицательность. Е_п уменьшается с возрастанием главного квантового числа п и орбитального радиуса r_орб.

Орбитальное квантовое число l. Число l может принимать целочисленные значения: l = 0, 1, 2, п - 1, т.е. максимальное значение l не превышает п - 1, где п - главное квантовое число.

Величина l определяет форму атомной орбитали и орбитальный подуровень энергии E_nl - главного энергетического уровня атома при данном п. При l = 0 форма орбитали сферическая и называется s-орбиталью. При l = 1 орбиталь имеет форму песочных часов (гантели) и называется р-орбиталью. При l = 2 форма орбитали четырехлопастная и называется d-орбиталью.

У р-орбиталей имеется узел, а у d-орбиталей узловые плоскости, где волновые функции равны нулю. Знаки лопастей чередуются. При п = 1 имеется только одна s-орбиталь и отсутствуют другие подуровни энергии и орбитали. При п = 2 имеются 2s (l = 0)- и 2р (l = 1)-орбитали разной ориентации. Им соответствуют энергетические подуровни Е_2s" Е_2р. При п = 3 имеются одна 3s (l = 0)-, 3р (l = 1)- и 3d (l = 2)-орбитали разных ориен-таций. Им соответствуют энергетические подуровни E_3s, Е_3p' E_3d.

Рис. 3.2. Пространственная форма s-, p-, d-атомных орбиталей

Размер атомных орбиталей разной формы возрастает с увеличением п.

Магнитное квантовое число m. Число т принимает целочисленные значения: 0, ±1, ±2, ±l. Определяют ориентацию орбиталей в пространстве, их число на данном орбитальном подуровне E_nl и магнитный энергетический подуровень E_nlm. На каждом орбитальном подуровне Е (l = 1) имеется три п_р-орбитали с ориентацией вдоль осей х, у, z. Например, при п= 2 подуровню E_2l(l = 1) соответствуют орбитали 2р_х(m = ±1), 2р_у(m = -1) и 2р_z(m = 0) (рис. 3.3).

При п = 3 подуровню Е₃₁ (l = 2) отвечают пять орбиталей разных ориентаций.

Рис. 3.3. Ориентация р-атомных орбиталей при разных значениях магнитного квантового числа т

Спиновое квантовое число s. Число s принимает два значения: +0,5 и -0,5. Характеризует собственное вращательное движение электрона. На каждой атомной орбитали двум значениям S = ± 0,5 отвечает вращение по часовой и против часовой стрелки. Соответственно имеются два спиновых подуровня энергии E_nlms.

Четыре квантовых числа n, l, m, s характеризуют различные типы пространственного квантования при движении одного электрона в атоме и определяют соответствующие квантовые энергетические уровни.

Орбиталь φ_nlm и соответствующий энергетический уровень E_nlm, определяемый четырьмя квантовыми числами п, l, m, s,называют квантовым состоянием электрона в атоме.

№26 Спин электрона, протона и элементарных частиц Спин был обнаружен в экспериментах Штерна и Герлаха (рис 1) при прохождении узкого пучка атомов водорода, находящихся в s - состоянии через сильное неоднородное магнитное поле. В этом состоянии l =о, момент импульса 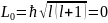и магнитное поле не должно было влиять на движение атомов. Однако пучок атомов расщепляется на два пучка, следовательно, было обнаружено пространственное квантование механического момента, не связанного с орбитальным движением электрона.

Спин электронов и всех других микрочастиц следует рассматривать как внутреннее неотъемлемое квантовое свойство микрочастицы: подобно тому как частицы имеют массу, а заряженные частицы имеют заряд, они имеют еще и спин. Спин , как механический момент, квантуется по закону:

- спиновое квантовое число.

С ним связан собственный магнитный момент 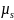. (2).

Проекция может принимать 2s+1 ориентаций. Так как опыты Штерна и Герлаха обнаружили только две ориентации спина, то 2s+1=2, откуда: .

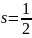Проекция 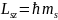, где - магнитное спиновое квантовое число,которое может иметь только два значения:

Спин – это квантовая величина, не имеющая классического аналога.

Таким образом, состояние электрона в атоме определяется набором четырех квантовых чисел: главного n (n=1,2,3,…..)

oрбитального l (l=0,1,2,…n-1)

магнитного m (m=-l,…0, +l)

магнитного спинового ( )

Вот уже более 25 лет физики пытаются ответить на вопрос о спиновой структуре протона.

Известно, что протон состоит из трех кварков. И первоначально ученые предполагали, что спин протона был суммой спинов трех составляющих его кварков. Но в 80-е годы прошлого столетия экспериментальным путем было выяснено: вклад кварков в суммарный спин протонов частичен. Тогда откуда берется остальная часть спина протона? В этом вопросе и суть так называемого кризиса спина протона («спиновой загадки»), над которой ученые бьются до сих пор. До настоящего времени было выдвинуто предположение, что появлению спина способствуют глюоны, которыми соединяются кварки внутри протона. Эту идею поддерживает ряд исследований на Релятивистском коллайдере тяжелых ионов (RHIC) в Брукхейвенской национальной лаборатории в Аптоне (штат Нью-Йорк). В ходе этих исследований анализируются столкновения протонов.

Мир кварков и глюонов

Глюоны дают внутри протона сильное ядерное взаимодействие, они являются той фундаментальной силой, которая связывает кварки. Спин глюона равен единице. И в зависимости от направления, в котором вращаются глюоны, можно было бы составить оставшуюся часть спина протона.

Измерить глюоны довольно непросто. Релятивистский коллайдер — единственная возможность это сделать, так как он единственный ускоритель частиц, который построен для столкновения «спин-поляризованных» протонов. То есть в нем спин всех частиц будет в одном направлении, когда они столкнутся. Так, к примеру, на более мощном швейцарском Большом адронном коллайдере спин частиц не выравнивается.

Взаимодействие двух столкнувшихся протонов контролируется мощной силой, и глюоны принимают в этом непосредственное участие. Если спин глюона — важная составляющая спина протона, то направление спинов сталкивающихся протонов влияет на результат. Ученые ожидали, что столкновение между двумя протонами, спины которых выровнены, произойдет на другой частоте, чем тогда, когда сталкиваются протоны со спинами, направленными в противоположные стороны. И последние данные с RHIC подтвердили: разница есть.

«Если нет определенных позиций, разница будет равна нулю, — говорит физик Хуан Рохо из Университета Оксфорда. — Если асимметрия не нулевая, распределение спина не будет тривиальным».

Команда Рохо рассчитала, что глюоны, вероятно, вносят половину спина в свойства протона.

Даниель де Флориан из Университета Буэнос-Айреса, опубликовавший в июле одну из новых работ на эту тему, вместе со своими коллегами проанализировал те же данные с RHIC. Но они применили другой математический анализ для расчета вклада глюонов. Однако выводы ученых схожи. Вклад спина глюонов в спин протона существенно важен.

«Эти данные впервые показали, что поляризация глюонов ненулевая; глюоны поляризованы. В принципе, они могут быть ответственны за остаток спина протона, но неопределенность крайне высока» – говорит Де Флориан.

№27 Электронная оболочка, подоболочки и уровни

Электронная оболочка атома — область пространства вероятного местонахождения электронов, характеризующихся одинаковым значением главного квантового числа n и, как следствие, располагающихся на близких энергетических уровнях. Число электронов в каждой электронной оболочке не превышает определенного максимального значения.

Порядок заполнения электронных оболочек (орбиталей с одинаковым значением главного квантового числа n) определяется правилом Клечковского, порядок заполнения электронами орбиталей в пределах одного подуровня (орбиталей с одинаковыми значениями главного квантового числа n и орбитального квантового числа l) определяется Правилом Хунда.

Квантовые характеристики электрона. Теория Бора приписывала четырем электронным оболочкам К, L, M и N квантовое число и, равное соответственно 1, 2, 3 и 4. Эти числа соответствуют повышающимся энергетическим уровням оболочек.

Однако внимательное рассмотрение атомных спектров показывает, что линии, обусловленные переходами между такими квантовыми энергетическими уровнями, на самом деле расщеплены на более тонкие линии. Это указывает, что электронные оболочки в действительности расщеплены на подоболочки, каждая со своим собственным квантовым энергетическим уровнем. Электронные подоболочки получили обозначения по типам соответствующих им линий в атомных спектрах, а именно:

s-подоболочка названа по «резкой» (sharp) s-линии р-подоболочка названа по «главной» (principal) р-линии d-подоболочка названа по «диффузной» (diffuse) d-линии f-подоболочка названа по «фундаментальной» (fundamental) f-линии

s-Подоболочка состоит из одной s-орбитали. р-Подоболочка состоит из трех р-орбиталей (см. рис. 1.18), а d-подоболочка-из пяти d-орбиталей.

Линии, обусловленные переходами между этими подоболочками, испытывают дальнейшее расщепление, если атомы элементов помещены во внешнее магнитное поле. Это расщепление называется эффектом Зеемана. Экспериментально установлено, что указанное расщепление возможно только для р-, d- и f-подоболочек. Каждый энергетический уровень, на который они расщепляются в магнитном поле, соответствует одной орбитали в подоболочке. Магнитное поле не оказывает влияния на s-подоболочку, так как она состоит всего из одной s-орбитали сферической формы.

В отсутствие магнитного поля все орбитали одной подоболочки имеют одинаковую энергию. Орбитали, имеющие одинаковую энергию, называются вырожденными.

Строение электронных оболочек атомов

Законы, по которым "живут"частицы микромира (электроны, нуклоны, атомы, молекулы) сильно отличаются от законов макромира (нашего мира – мира физических тел). Многое в поведении этих частиц наш мозг, эволюционировавший в макромире, просто не в состоянии себе представить. Поэтому с некоторыми особенностями таких частиц, особенностями, которые нам кажутся неожиданными и странными, нам придется просто смириться.

Из основного свойства заряженных тел и частиц следует, что неподвижными электроны в атоме быть не могут. Ведь в этом случае они, притянувшись к ядру, просто упали бы на него, и атом перестал бы существовать. Следовательно, электроны в атоме движутся. Но уже Резерфорду было ясно, что просто вращаться вокруг ядра электроны не могут. В то время уже были известны законы электродинамики, в соответствии с которыми вращающийся вокруг ядра электрон обязан постепенно терять свою энергию, что должно приводить в конце концов, к его падению на ядро. Эта исключительно сложная проблема хоть и не всегда последовательно, но была решена в первой трети ХХ века в результате работ многих выдающихся физиков: Нильса Бора, Альберта Эйнштейна, Эрвина Шрёдингера, Вернера Гейзенберга, Макса Борна и многих других ученых. С основными выводами из этих работ мы с вами и познакомимся.

Изучая электроны, атомы, молекулы, а также процессы их взаимодействия, мы будем использовать некоторые модели, позволяющие нам все же получить более или менее наглядное представление об изучаемых объектах. При этом необходимо помнить, что любая модель описывает реальность с той или иной степенью точности и может быть использована только в той области, для которой она создавалась.

Из частиц микромира нас интересует прежде всего электрон. И хотя свойства, проявляемые электроном в различных условиях, вы будете изучать в курсе физики, мы с вами кратко познакомимся стремя основными особенностями поведения электронов в атоме.

П ервая особенность.Энергия свободного электрона, так же как и энергия тела, может изменяться непрерывно, но энергия связанного электрона, в частности электрона в атоме, может принимать только вполне определенные значения.

С хематически это изображено на рис. 6.1, где слева на оси энергии жирной линией показаны возможные значения энергии свободного электрона, а справа на такой же оси отдельными точками – значения энергии электрона в атоме. Таким образом, электрон в атоме может находиться только во вполне определенных состояниях.

При переходе электрона из одного состояния в другое энергия поглощается или выделяется порциями –квантами энергии. Поэтому первая особенность поведения электрона часто называется принципом квантования его энергии. Эта особенность была постулирована датским физиком Нильсом Бором в 1913 году и в дальнейшем получила блестящее экспериментальное подтверждение.

Вторая особенность. Электрон в одних случаях проявляет свойства частицы вещества, а в других – волновые свойства. Такая двойственность поведения электрона и других микрочастиц (дуализм) – одно из общих свойств материи (и вещества, и поля). Оно называется "корпускулярно-волновой дуализм"или "дуализм волна-частица ".

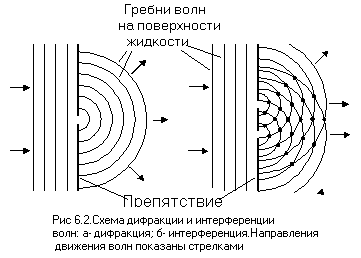
Волновые свойства электрона проявляются, например, при прохождении потока электронов через тончайшую кристаллическую пленку. Поток электронов ведет себя так, как будто через эту пленку прошли волны, то есть, подвергается дифракции(огибание волнами встречающегося на их пути препятствия ,если его размер сопоставим с длиной волны) и интерференции(увеличение гребней и уменьшение впадин волн при наложении их друг на друга) (смысл этих явлений понятен из рисунка 6.2, на котором показаны схемы дифракции и интерференции  волн на поверхности воды при встрече препятствия с одним, или двумя отверстиями). Эту особенность поведения электрона предсказал французский физик Луи де Бройль в 1924 году, а в 1926 году американский физик Клинтон Девиссон впервые наблюдал дифракционную картину при взаимодействии потока электронов с металлами. В настоящее время волновые свойства электронов широко используются при исследовании строения различных веществ.

 

Третья особенность. Чем с большей точностью определяют положение электрона в пространстве, тем с меньшей точностью можно определить его скорость. И наоборот, чем с большей точностью определяют скорость электрона(абсолютную величину и направление), тем с меньшей точностью можно определить его положение в пространстве. Это утверждение, а оно справедливо и для других микрочастиц, называется "принцип неопределенностей". Этот принцип был сформулирован немецким физиком Вернером Гейзенбергом в 1927 году. Принцип неопределенностей "лишает "летящий электрон траектории. Действительно, если мы в какой-то момент точно знаем положение электрона, то мы принципиально ничего не знаем о его скорости и в следующий момент времени можем обнаружить электрон в любой другой точке атома, правда, с разной вероятностью.

Теорию вероятностей изучает математика, а мы лишь воспользуемся несколько упрощенным определением этого понятия.

Вероятность – отношение числа событий с "благоприятным "исходом к общему числу событий.

№28 КВАНТОВОМЕХАНИЧЕСКОЕ ОБЪЯСНЕНИЕ ТАБЛИЦЫ МЕНДЕЛЕЕВА

Периодическая таблица элементов, составленная Менделеевым в 1869 г., играет важную роль при исследовании структуры и свойств вещества. Законами классической физики и химии невозможно объяснить закономерности этой таблицы.

Только после появления квантовой механики эти закономерности были объяснены. Как известно, энергия электронов в многоэлектронных атомах, зависит от квантовых чисел 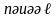. Последовательность расположения электронных оболочек имеет вид:

- это идеальное заполнение оболочек.

Опыты показывают, что начиная с 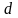оболочек эта последовательность нарушается.

Для объяснения закономерностей таблицы Менделеева используется, так называемый, принцип построения:

1. Заполнение электронных оболочек начинается с орбитали с наименьшей энергией и продолжается по мере возрастания энергии.

2. Согласно принципу Паули, на каждой атомной орбитали (АО), с определенным набором квантовых чисел n.l и 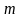находится по 2 электрона с противоположными спинами.

3. Правило Хунда. Для данной электронной конфигурации: наименьшей энергией обладает (уровень) терм, с наибольшей мультиплетностью, т.е. с наибол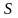ьшим значением (полный спиновый момент или полный спин) и с наибольшим значением 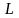(суммарный орбитальный момент) при данной .

Используя эти правила, построим электронную конфигурацию некоторых атомов, начиная с водорода:

Третий электрон при заполнении электронных оболочек не может находиться на 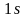орбитали, в соответствии с принципом Паули.

В атоме третий электрон находится либо н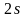а , либо на орбитали.

Экспериментально установлено, что энергия , однако:

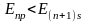
Таким образом, третий электрон находится на орбитали; тогда электронная конфигурация будет иметь вид:

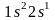
Квантовые числа четвертого электрона:

Известно, что – орбитали состоят из 3-х эквивалентных орбиталей: 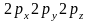. Пятый электрон бора с одинаковой вероятностью может находиться в одной из них. Аналогичная картина имеет место в атоме углерода.

В некоторых случаях сперва заполняются оболочки с большим значением главного квантового числа n.

Для объяснения этого Клечковский предложил следующее правило:

Если для 2-х уровней энергии одинаково, то первым заполняется уровень с меньшим n например:

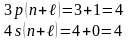
Используя правило Клечковского и принцип построения таблицы Менделеева, можно представить заполнение электронных оболочек следующим образом:

Период	Электронное состояние	Число электронов
1		2
2		8
3		8
4		18
5		18
6		32
7	…	--

Таблица Менделеева состоит из 7 периодов. Первый элемент каждого периода входит в I группу. Всего групп – 8.

Каждый период начинается с заполнения 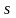– оболочки и заканчивается заполнением – оболочки.
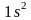
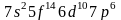