1.Основное противоречие между экспериментальными данными и теорией теплового излучения, которое было к началу 20в.

Основываясь на непрерывном характере испускания электромагнитных волн и на законе равновесного распределения энергии по степеням свободы, были теоретически получены две формулы для излучательной способности АЧТ:

1. Формула Вина:         U_λ,T = a₁ · λ^-3 · exp(-a₂/λT)                   (9),

где a₁, a₂ – постоянные величины.

2. Формула Рэлея-Джинса: U_λ,T = a₃ · λ^-3 · k · T                       (10),

где k – постоянная Больцмана.

Опытная проверка показала, что для данной температуры формула Вина верна для коротких волн, когда λ·T→0 и дает резкие расхождения с опытом в области длинных волн. Формула Рэлея-Джинса оказалась верна для длинных волн и совершенно не применима для коротких (рис.7)

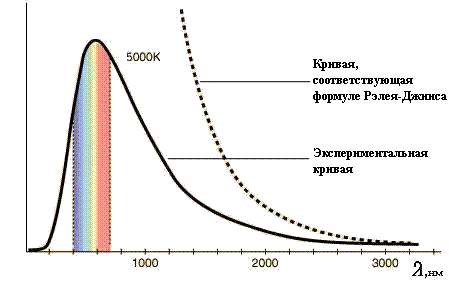
Рис. 7.

Так как формула Рэлея-Джинса, опирающаяся на классическую физику, в резком противоречии с опытом, приводит к заключению, что в спектре теплового излучения большая часть энергии приходится на фиолетовую часть спектра, то это положение было названо Эренфестом «Ультрафиолетовой катастрофой».

Подводя итог сказанному, видим, что классическая физика в теории теплового излучения потерпела решительное поражение. Таким образом, к концу 19 столетия существовали две формулы, полученные теоретически, каждая из которых соответствовала экспериментальным данным в ограниченном участке спектра, но ни одна из них не описывала всю экспериментальную кривую

2.Основные следствия из формулы Планка для теплового излучения.

Величина кванта энергии ε пропорциональна частоте излучения  (обратно пропорциональна длине волны λ :

ε = h·ν = h·c/λ                                                            (11).

Коэффициент пропорциональности h = 6,626176·10^-34 Дж·с называется постоянной Планка. Именно крайне малая величина h является причиной того, что дискретность, требуемая законами атомной физики, совершенно не сказывается при изучении макроскопических явлений.

Окончательное выражение, полученное Планком для излучательной способности АЧТ, имеет вид:

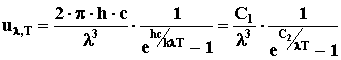     (12),

где C₁ = 2πhc, C₂ = hc/k, где c – скорость света в вакууме; k – постоянная Больцмана.

Кривая, соответствующая формуле (12) совпадает с экспериментальной кривой u_λ,T (рис.7). Зная величину постоянной Планка h и частоту или длину волны света, мы можем вычислить величину кванта энергии для любого участка спектра АЧТ.

Из формулы Планка (12) как частный случай получаются закон Стефана-Больцмана и закон Вина. Действительно для светимости АЧТ получаем:

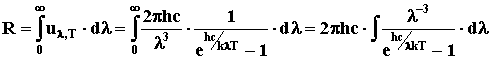
Вводя новую переменную x = hc/(λkT), преобразуем выражение:

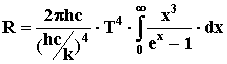
Обозначив произведение всех постоянных множителей через σ, получим формулу R = σ·T⁴, соответствующую закону Стефана-Больцмана. Расчет σ по этой формуле дает результат, совпадающий с эмпирическим значением постоянной Стефана-Больцмана.

Закон смещения Вина и его константу можно получить из формулы Планка нахождением максимума функции u_λ,T, для чего берется производная от u_λ,T по λ и приравнивается 0. Вычисление приводит к формуле:

.

Расчет постоянной b₁ по этой формуле дает результат, совпадающий с эмпирическим значением постоянной Вина.

3.Свойства фотоэлектрического эффекта, которые противоречат волновой природе света.

Качественное объяснение фотоэффекта с волновой точки зрения на первый взгляд не должно было представлять трудностей. Действительно, под действием поля световой волны в металле возникают вынужденные колебания электронов, амплитуда которых(например, при резонансе) может быть достаточной для того, чтобы электроны покинули металл; тогда и наблюдается фотоэффект. Кинетическая энергия вырываемого из металла электрона должна была бы зависеть от интенсивности падающего света, так как с увеличением последней электрону передавалась бы большая энергия. Однако этот вывод противоречит 2 закону фотоэффекта

-Максимальная начальная скорость(мах кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой.

Так как по волновой теории, энергия, передаваемая электронам, пропорциональна интенсивности света, то свет любой частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла; иными словами, красной границы фотоэффекта не должно быть, что противоречит 3 закону фотоэффекта

-Для каждого вещества существует красная граница фотоэффекта,т.е. минимальная частота света ниже которой фотоэффект невозможен.

Также, волновая теория не смогла объяснить безынерционность фотоэффекта, установленную опытами. Т.о. фотоэффект необъясним с точки зрения волновой теории света.

4.Следствия из формулы Эйнштейна для фотоэффекта.

Уравнение Эйнштейна позволяет объяснить 2 и 3 законы фотоэффекта

-Максимальная начальная скорость(мах кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой.

-Для каждого вещества существует красная граница фотоэффекта,т.е. минимальная частота света ниже которой фотоэффект невозможен.

Из формулы следует, что мах кинетическая энергия фотоэлектрона линейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности (числа фотонов), так как ни А, ни V, от интенсивности света не зависят(2 зак). Так с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается(для данного металла А=const), то при некоторой достаточно малой частоте V=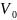 кинетическая энергия фотоэлектронов станет равной нулю и фотоэффект прекратится(3 зак). Тогда

И есть красная граница фотоэффекта для данного металла. Она зависит лишь от работы выхода электрона,т.е. от химич природы вещ-ва и и состояния его поверхности.

5.Формула Комптона, описывающая упругое рассеяние излучения на свободных электронах. ЭффектКомптона  – рассеяние электромагнитного излучения на свободном электроне, сопровождающееся уменьшением частоты излучения .     Комптоновское рассеяние – это рассеяние на свободном электроне отдельного фотона с энергией Е = hν = hc/λ (h – постоянная Планка, ν – частота электромагнитной волны, λ – её длина, с – скорость света) и импульсом р = Е/с. Рассеиваясь на покоящемся электроне, фотон передаёт ему часть своей энергии и импульса и меняет направление своего движения. Электрон в результате рассеяния начинает двигаться. Фотон после рассеяния будет иметь энергию Е' = hν' (и частоту) меньшую, чем его энергия (и частота) до рассеяния. Соответственно после рассеяния длина волны фотона λ' увеличится. Из законов сохранения энергии и импульса следует, что длина волны фотона после рассеяния увеличится на величину

,

где θ – угол рассеяния фотона, а m_e – масса электрона h/m_ec = 0.024 Å называется комптоновской длиной волны электрона.     Изменение длины волны при комптоновском рассеянии не зависит от λ и определяется лишь углом θ рассеяния γ-кванта. Кинетическая энергия электрона определяется соотношением

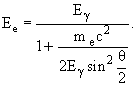
    Эффективное сечение рассеяния γ-кванта на электроне не зависит от характеристик вещества поглотителя. Эффективное сечение этого же процесса, рассчитанное на один атом, пропорционально атомному номеру (или числу электронов в атоме) Z.     Сечение комптоновского рассеяния убывает с ростом энергии γ-кванта: σ_k ~ 1/E_γ.

Расчет эффекта Комптона

П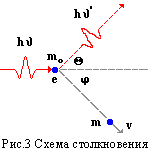 усть фотон с энергией hν падает на покоящийся электрон (см. рис.3).  Запишем уравнения, выражающие законы сохранения энергии и импульса: 1.энергия до столкновения (энергия фотона hν плюс энергия покоя электрона) должна равняться энергии после столкновения (энергия hν' рассеянного фотона плюс полная энергия получившего отдачу электрона)

hν + m_oc² = hν' + mc²,  (1)

где m_o - масса покоящегося электрона, m - масса движущегося электрона, с - скорость света;

2.импульс падающего фотона p должен равняться сумме импульсов электрона p_e и рассеянного фотона p'

p = p' + p_e  (2)

Энергия фотона связана с импульсом соотношением

|p| = hν/c.  (3)

Преобразуем выражение (1): перенесем энергию рассеянного кванта в левую часть, выразим энергии квантов через импульсы в соответствии с (3), разделим обе части равенства на c и возведем в квадрат

(p - p' + m_oc)² = (mc)².  (4)

В законе сохранения импульса (2) перенесем импульс рассеянного кванта в левую часть и возведем в квадрат обе части равенства

p² - 2pp' + p'² = p_e².  (5)

После вычитания последнего равенства из (4) получим

-2pp' + 2pp'cosΘ + 2pm_oc - 2p'm_oc + m_o²c² = m²c² - p_e²  (6)

Квадрат полной энергии электрона

E_e² = (mc²)² = p_e²c² + m_o²c⁴.

Учитывая это, замечаем, что правая часть (6) равна m_o²c². Точно такое же слагаемое есть и в левой части (6). После сокращений получим выражение для модуля импульса рассеянного фотона

p' = p/[1 + (p/mc)(1 - cosΘ)].  (7)

Поскольку импульс фотона p = h/λ, получаем окончательное выражение для изменения длины волны рассеянного фотона

λ' - λ = (h/m_оc)(1 - cos Θ).  (8)

Величина h/m_oc называется комптоновской длиной волны электрона, ее численное значение равно h/m_oc = 2.4263096(15) ·10^-12 м. Это длина волны фотона с энергией, равной m_oc² - энергии покоя электрона.

6.Общая закономерность, объединяющая спектральные серии Лаймана,Бальмера,Пашена, Брэкета,Пфунда и Хамфри. Исследования спектров излучения разреженных газов (т. е. спектров излучения отдель­ных атомов) показали, что каждому газу присущ определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Самым изученным является спектр наиболее простого атома — атома водорода. Швейцарский ученый И. Бальмер (1825—1898) подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:     (209.1) где R'=1,10107 м–1 — постоянная Ридберга.* Taк как  = c/, то формула (209.1) может быть переписана для частот: 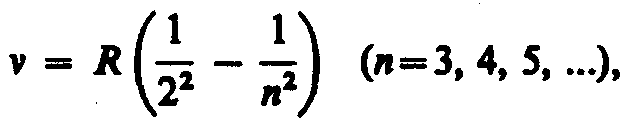   (209.2) где R=R'c=3,291015 с–1 — также постоянная Ридберга. * И. Ридберг (1854—1919) — шведский ученый, специалист в области спектроскопии. Из выражений (209.1) и (209.2) вытекает, что спектральные линии, отличающиеся различными значениями п, образуют группу или серию линий, называемую серией Бальмера. С увеличением n линии серии сближаются; значение n =  определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр. В дальнейшем (в начале XX в.) в спектре атома водорода было обнаружено еще несколько серий. В ультрафиолетовой области спектра находится серия Лаймана: 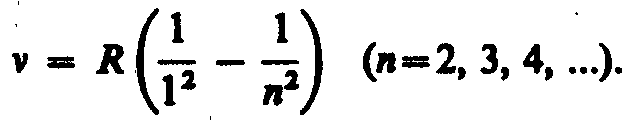В инфракрасной области спектра были также обнаружены: 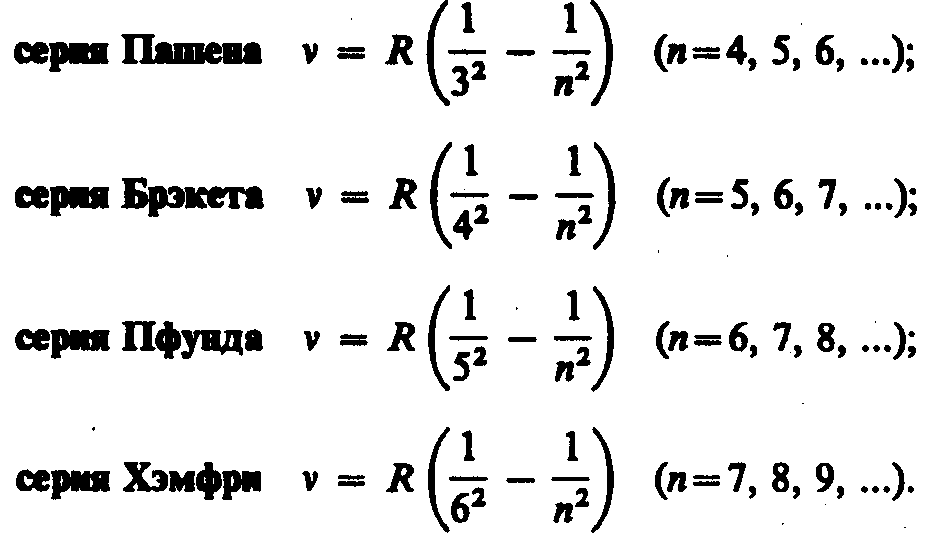Все приведенные выше серии в спектре атома водорода могут быть описаны одной формулой, называемой обобщенном формулой Бальмера: 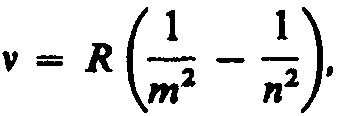     (209.3) где т имеет в каждой данной серии постоянное значение, m = 1, 2, 3, 4, 5, 6 (определяет серию), п принимает целочисленные значения начиная с т+1 (определяет отдельные линии этой серии). Исследование более сложных спектров — спектров паров щелочных металлов (на­пример, Li, Na, К) — показало, что они представляются набором незакономерно расположенных линий. Ридбергу удалось разделить их на три серии, каждая из которых располагается подобно линиям бальмеровской серии. Приведенные выше сериальные формулы подобраны эмпирически и долгое время не имели теоретического обоснования, хотя и были подтверждены экспериментально с очень большой точностью. Приведенный выше вид сериальных формул, удивитель­ная повторяемость в них целых чисел, универсальность постоянной Ридберга свиде­тельствуют о глубоком физическом смысле найденных закономерностей, вскрыть который в рамках классической физики оказалось невозможным.

7.Основное противоречие между классической электродинамикой и планетарной моделью атома, предложенной Э.Резерфордом. Атом по Резерфорду - это положительно заряженное ядро в центре атома и электроны на орбитах вокруг ядра - характер движения электронов определяется действием кулоновских сил со стороны ядра - диаметр ядра в 100000 раз меньше диаметра атома - масса ядра составляет 99,4% от массы всего атома - заряд ядра составляет 99,4% от заряда всего атома - заряд ядра по модулю равен сумме зарядов электронов, поэтому атом в целом нейтрален. Однако, возникли противоречия между законами классической механики и электродинамики и предложенной Резерфордом моделью атома: 1. Согласно классической механике по модели атома Резерфорда атомы должны быть неустойчивы, т.к.: электроны движутся по орбитам с ускорением, поэтому должны излучать электромагнитные волны излучая, должны терять энергию в результате должны упасть на ядро  тогда атом должен прекратить свое существование. Однако, реальные атомы устойчивы и в невозбужденном состоянии могут существовать неограниченно долго, не излучая электромагнитные волны. 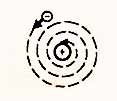2. По законам классической электродинамики, электрон, приближаясь к ядру, должен двигаться все быстрее, излучая все более короткие электромагнитные волны, поэтому спектр излучения атома должен быть сплошным. Однако, у реальных атомов спектр излучения является линейчатым.

8. Соотношения неопределённостей – фундаментальные соотношения квантовой механики, устанавливающие предел точности одновременного определения так называемых дополнительных физических величин, характеризующих систему (например, координаты и импульса). В упрощённой формулировке эти соотношения утверждают, что дополнительные физические величины не могут быть одновременно точно определены. Неопределённостей соотношения являются следствием двойственной, корпускулярно-волновой природы частиц материи, отражением вероятностной (статистической) сути квантовой механики.

Неопределённостей соотношения имеют вид неравенств, например, ΔxΔp > ћ = h/2π, где Δx – неопределённость координаты (частицы или системы), Δp – неопределённость её импульса, а h = 6.6·10-34 Дж.с = 4.1·10-15 эВ.с - постоянная Планка. Отсюда видно, что произведение неопределённостей координаты и импульса не может быть меньше ћ, и никаким усовершенствованием методов наблюдения нельзя преодолеть этот рубеж. Увеличение точности определения координаты неизбежно ведёт к потере точности определения импульса. Предельная точность одновременного определения координаты и импульса даётся соотношением Δx·Δp ≈ ћ.

Другая важная пара дополнительных физических величин – энергия Е и время t. Соотношение неопределённостей для них имеет вид ΔЕ·Δt > ћ. Это соотношение для релятивистских системы или частиц (двигающихся со скоростью близкой к скорости света с) может быть получено из соотношения неопределённостей для координаты и импульса простым преобразованием: Δx/с·Δpс = ΔtΔЕ > ћ. Полученное соотношение для времени и энергии можно трактовать следующим образом. Для того, чтобы определить энергию частицы (системы) с точностью ΔЕ, необходимо проводить измерения в течение промежутка времени Δt > ћ/ΔЕ. Следствием этого соотношения является возможность виртуальных (ненаблюдаемых) процессов, лежащих в основе механизма взаимодействия частиц в квантовой теории поля. Две частицы взаимодействуют, обмениваясь с нарушением баланса энергии на величину ΔЕ виртуальным (ненаблюдаемым) переносчиком взаимодействия, существующим в течение времени Δt < ћ/ΔЕ.

Другая трактовка соотношения ΔЕΔt ≈ ћ связана с понятием времени жизни нестабильного (распадающегося состояния системы или частицы). Так, если квантовая система в дискретном энергетическом состоянии живёт в среднем время τ ≈ Δt, то энергетическая ширина уровня Г даётся соотношением Г ≈ ΔЕ ≈ ћ/Δt ≈ ћ/τ.

В силу крайней малости константы Планка ћ, соотношения неопределённостей не играют практически никакой роли для макроскопических тел.

№9

10. Экспериментальное подтверждение идеи Луи де Бройля об универсальности корпускулярно-волнового дуализма, ограниченность применения классической механики к микрообъектам, диктуемая соотношением неопределенностей, а также противоречия ряда экспериментов с применяемыми в начале XX века теориями привели к новому этапу развития квантовой физики – созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств. Ее создание и развитие охватывает период с 1900 г. (формулировка Планком квантовой гипотезы) до 20-х годов XX века и связано, прежде всего, с работами австрийского физика Э. Шредингера, немецкого физика В. Гейзенберга и английского физика П. Дирака.

Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории. Можно ли волны де Бройля истолковывать как волны вероятности, т.е. считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону? Такое толкование волн де Бройля уже неверно, хотя бы потому, что тогда вероятность обнаружить частицу в некоторых точках пространства может быть отрицательна, что не имеет смысла.

Чтобы устранить эти трудности, немецкий физик М. Борн в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая . Эту величину называют также волновой функцией (или -функцией). Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля: (4.3.1)

где , где – функция комплексно-сопряженная с Ψ.

Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волны де Бройля) определяет вероятность нахождения частицы в момент времени в области с координатами x и dx, y и dy, z и dz.

Итак, в квантовой механике состояние частицы описывается принципиально по-новому – с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых . (4.3.2)

Величина (квадрат модуля Ψ-функции) имеет смысл плотности вероятности, т.е. определяет вероятность нахождения частицы в единице объема в окрестности точки, имеющей координаты x, y, z. Таким образом, физический смысл имеет не сама Ψ-функция, а квадрат ее модуля , которым определяется интенсивность волн де Бройля.

Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме о сложении вероятностей, равна:

.

Т.к. определяется как вероятность, то необходимо волновую функцию Ψ представить так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей: (4.3.3)

где данный интеграл вычисляется по всему бесконечному пространству, т.е. по координатам x, y, z от до . Таким образом, условие нормировки говорит об объективном существовании частицы во времени и пространстве.

Чтобы волновая функция являлась объективной характеристикой состояния микрочастицы, она должна удовлетворять ряду ограничительных условий. Функция Ψ, характеризующая вероятность обнаружения микрочастицы в элементе объема, должна быть:

· конечной (вероятность не может быть больше единицы);

· однозначной (вероятность не может быть неоднозначной величиной);

· непрерывной (вероятность не может меняться скачком).

Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями , , … , то она может находиться в состоянии, описываемом линейной комбинацией этих функций:

,

где (n = 1, 2, 3…) – произвольные, вообще говоря, комплексные числа.

Сложение волновых функций (амплитуд вероятностей, определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей.

Волновая функция Ψ является основной характеристикой состояния микрообъектов. Например, среднее расстояние электрона от ядра вычисляется по формуле

,

где вычисления проводятся, как и в случае (4.3.3).

11. Как, зная волновую функцию предсказать результат измерения соответствующей физической величины у частицы, находящейся в рассматриваемом квантовом состоянии? Для получения информации о физических величинах, связанных с движущейся частицей, в квантовой механике разработан специальный математический аппарат, который использует представления об операторах физических величин и результатах их действия на волновые функции.

В работах М.Борна, П.Дирака и др. был сформулирован второй постулат квантовой механики, утверждающий, что каждой физической величине соответствует определенный оператор этой физической величины. При этом соотношения между операторами в квантовой механике имеют ту же структуру, что и соотношения между соответствующими им физическими величинами в классической механике.

Для расшифровки этого постулата дадим некоторые пояснения. Оператор - это математическое правило, следуя которому мы можем преобразовать одну функцию в другую. Задать оператор - это означает определить рецепт такого преобразования. Такое преобразование может быть простым умножением исходной функции на число или известную функцию, дифференцированием функции, перестановкой аргументов функции и др. В квантовой механике в качестве символа соответствующего оператора используется классическое обозначение физической величины, ставя над буквой "шляпку" в виде значка . Например, - это оператор координаты , - оператор проекции импульса на ось , - оператор потенциальной энергии и т.д. Оператор предполагается действующим на написанную вслед за ним функцию. В качестве таких функций в квантовой механике выступают волновые функции. При этом равенство двух функций в операторной форме будет записываться как равенство операторов: .

Определим операторы основных физических величин в квантовой механике.

1. Оператор координаты. Действие этого оператора на волновую функцию сводится к умножению ее на соответствующую координату, то есть.

. (3.27)

В символической операторной форме записи этих операций имеют вид

. (3.28)

Объединяя эти формулы, можно ввести векторный оператор , соответствующий радиусу-вектору в классической механике. Такой оператор формально рассматривается как некоторый вектор, имеющий в качестве компонент в декартовой системе координат операторы . Поэтому

. (3.29)

2. Оператор импульса. С помощью операций дифференцирования по координатам определим операторы проекций импульса, записав эти определения в символической операторной форме как

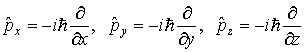. (3.30)

Все три формулы в (3.30) можно объединить в одну, введя векторный оператор импульса , который с учетом (3.30) запишется как

. (3.31)

Здесь

.

Используя соотношение классической механики

,

определим оператор квадрата импульса как

. (3.32)

Используя символ оператора Лапласа, запишем (3.32) в более компактном виде

. (3.33)

3. Оператор момента импульса. По формуле классической механики, определяющей момент импульса частицы как вектор , запишем выражения для его проекций на координатные оси:

.

Эти соотношения превратим в операторные, определяющие операторы проекций момента импульса

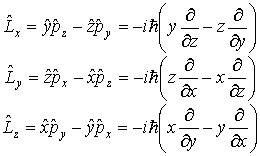. (3.34)

Оператор квадрата момента импульса можно построить по правилу

. (3.35)

Отметим, что задачи квантовой механики, обладающие сферической симметрией, удобнее решать не в декартовой, а в сферической системе координат , и . Переходя от декартовых координат к сферическим по обычным правилам замены переменных , , , формулы (3.34) и (3.35) можно преобразовать к следующему виду

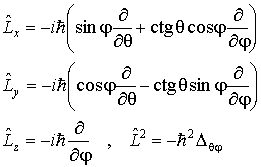. (3.36)

Здесь

- угловая часть оператора Лапласа в сферической системе координат.

4. Операторы энергий. Классическая формула связи кинетической энергии частицы с квадратом ее импульса

позволяет записать аналогичное соотношение между соответствующими операторами. Поэтому

. (3.37)

Если частица движется в стационарном силовом поле, и ее потенциальная энергия определена в любой точке пространства, то оператор потенциальной энергии определяется как оператор умножения на функцию , то есть

. (3.38)

Так как полная энергия частицы в классической механике есть сумма кинетической и потенциальной энергий, то в квантовой механике оператор полной энергии определяется как сумма операторов кинетической и потенциальной энергий. Поэтому

.

Раскрывая выражение для оператора квадрата импульса по формуле (3.33), запишем оператор полной энергии как

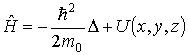. (3.39)

В классической механике полную энергию частицы, выраженную через ее координаты и импульс, называют функцией Гамильтона. Поэтому в квантовой механике оператор полной энергии называют оператором функции Гамильтона или просто гамильтонианом.

Гамильтониан является основным оператором квантовой механики, поскольку, выбирая конкретный вид гамильтониана, с учетом силового поля, действующего на частицу, мы формулируем на математическом языке все особенности квантовой системы. Поэтому и основное уравнение нерелятивистской квантовой механики - уравнение Шредингера (3.8) может быть записано в операторной форме

, (3.40)

содержащей гамильтониан .

Физическое содержание операторного метода в квантовой механике накладывает определенные ограничения на возможный вид квантовомеханических операторов. Пусть - оператор физической величины . Тогда для любых функций и и произвольных постоянных и должно выполняться равенство

. (3.41)

Операторы, обладающие таким свойством, называются линейными операторами. Свойство линейности операторов физических величин тесно связано с принципом суперпозиции квантовых состояний. Только использование в теории линейных операторов не нарушает этого принципа.

Оператором физической величины может быть только линейный самосопряженный (эрмитов) оператор. Только такому оператору соответствует действительная (не комплексная) физическая величина. Самосопряженным называют оператор, который совпадает со своим сопряженным оператором. В этом случае для произвольных функций и тождественно выполняется следующее интегральное равенство

. (3.42)

Таким образом, каждой физической величине в квантовой механике приводится в соответствие определенный линейный самосопряженный оператор. Непосредственной проверкой можно убедиться, что все приведенные выше квантовомеханические операторы обладают такими свойствами.

12. Свойства собственных функций операторов

Собственные функции операторов квантовой механики обладают следующими общими свойствами.

1. Если оператор имеет дискретный спектр собственных значений , то собственные функции этого оператора удовлетворяют уравнению

Уравнение, комплексно сопряжённое (18) для квантового числа m,

Умножаем (18) и (19) слева на и соответственно, интегрируем по всей области пространства и вычитаем из первого второе. В результате получаем

Отсюда следует

при n m - условие ортогональности собственных функций, соответствующих разным собственным значениям оператора.

Физический смысл ортогональности собственных функций заключается в том, что

при измерении физической величины с достоверностью получается значение в состоянии и - в состоянии .

Кроме того, в соответствии с (15) функции дискретного спектра всегда могут быть нормированы на единицу:

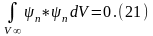
Соотношения (20) и (21) могут быть объединены:

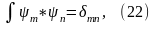
где символ Кронекера определяется следующим образом:

	{	1, если n = m;	(23)
		0, если n m.

Набор функций удовлетворяющий условию (22) , называется системой ортонормированных функций, т.е. ортогональных и нормированных.

2. Второе свойство собственных функций операторов заключается в том, что их совокупность образует полную систему функций. Это значит, что

любая функция , определенная в той же области переменных, что и собственные функции , может быть представлена в виде ряда

где суммирование выполняется по всем значениям квантового числа n.

Чтобы найти коэффициенты разложения , умножим (24) слева на и проинтегрируем по всему пространству:

Меняя индексы m на n, получаем выражение для коэффициентов разложения:

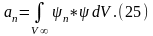
Умножим (24) на комплексно сопряженное выражение

и проинтегрируем по всему пространству:

или

Соотношение (27) - критерий того, что система функций норми­рована на единицу. Таким образом, в соответствии с (4)

вероятность на­хождения физической величины в состоянии со значением равна квад­рату модуля коэффициента в разложении (24), т.е. определяется ин­тенсивностью , с которой собственное состояние представле­но в состоянии .

14. Ортогональные операторы

Линейный оператор называется ортогональным , если

Для того чтобы оператор был ортогональным, необходимо и достаточно, чтобы его матрица в ортонормированном базисе была ортогональной.

Ортогональные операторы и только они сохраняют длину вектора, т. е.

Сопряженные операторы

Оператор называется сопряженным линейному оператору , если

Оператор также является линейным оператором. Если f в некотором ортогональном базисе имеет матрицу A, то в этом базисе оператор имеет матрицу .

Свойства сопряженных операторов: (f - невырожденный).

Самосопряженные операторы

Линейный оператор называется самосопряженным (симметрическим), если

Для самосопряженного оператора

Оператор является самосопряженным тогда и только тогда, когда его матрица в некотором ортонормированном базисе симметрическая.

Свойства самосопряженных операторов: 1) самосопряженный оператор имеет только действительные собственные числа; 2) всякий самосопряженный оператор является оператором простой структуры; 3) для всякого самосопряженного оператора существует ортонормированный базис, состоящий из собственных векторов этого оператора.