60. Выбор объема перераспределения

В цикле пересчета поставки чередуются с изъятием продукта. Если в какую-то

клетку поставляется единиц продукта, то из соседней по отношению к ней

должны быть изъяты эти единиц. Это делается для того чтобы соблюдался

баланс между поставками и потребностями в таблице. Значение определяется

как минимальная величина среди ранее сделанных поставок , откуда это

вычитается

61. Случай построения вырожденного построения при перераспределении поставок в транспортной задаче и избавление от вырожденности.

План называется вырожденным, если количество базисных клеток в

нем меньше, чем m + n − 1.

Если на каком-то этапе решения получился вырожденный план, то его

необходимо пополнить, проставив в недостающем числе клеток нулевую

перевозку и превратив, тем самым, эти клетки в базисные. Общий баланс и

суммарная стоимость перевозок плана при этом не изменятся. Однако прово-

дить пополнение плана, выбирая клетки произвольно, нельзя. Приведем ус-

ловия, которым должен соответствовать пополненный план.

• Циклом в транспортной таблице называется несколько клеток, со-

единенных замкнутой ломаной линией так, чтобы две соседние вершины ло-

маной были расположены либо в одной строке, либо в одном столбце. Лома-

ная линия может иметь точки самопересечения, но не в клетках цикла.

• План называется ациклическим, если его базисные клетки не содер-

жат циклов.

Доказано, что оптимальные планы являются ациклическими, поэтому и

первоначальный план также должен удовлетворять этому требованию.

Однако если план оказался вырожденным, то при его пополнении тре-

бование ацикличности необходимо учитывать.

62.Признак единственности оптимального распределения транспортной задачи и признак множества оптимальных распределений.

Если все свободные клетки имеют оценку ≤ 0, то оптимальное решение задачи найдено. Если все оценки незанятых клеток < 0, то оптимальный план единственный. Если некоторые оценки в оптимальном плане незанятых клеток =0, то план неединственный. Эти клетки можно сделать занятыми, но общая стоимость перевозки не изменится.

63. Алгоритм метода потенциалов.

Алгоритм решения транспортной задачи заключается в следующем:

- проверяется открытая или закрытая модель. Если задача открытая, то вводят фиктивного поставщика или фиктивного потребителя с нулевыми тарифами перевозок;

- составляют начальный опорный план (первоначальное распределение);

- проверяют на вырожденность (заполненных клеток должно быть m+n-1);

- находят потенциалы;

- находят оценки оптимальности незаполненных клеток;

- если есть «неблагоприятные» клетки, то для клетки с наибольшей оценкой строят цикл пересчета, определяют величину перераспределения 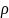(ро) и заполняют новую таблицу;

- если все свободные клетки имеют оценку ≤ 0, то оптимальное решение задачи найдено. Если все оценки незанятых клеток < 0, то оптимальный план единственный. Если некоторые оценки в оптимальном плане незанятых клеток =0, то план неединственный. Эти клетки можно сделать занятыми, но общая стоимость перевозки не изменится.