30. Идея симплекс метода, ее геометрическая иллюстрация.

Его идея основывается на следующих предположениях

-Указание способа построения начального опорного плана

-задается критерий с помощью которого начальный опорный план проверяется на оптимальность

-или проверяемый опорный план не является оптимальным, то указывается способ построения нового опорного плана более близкого к оптимальному.

31. Алгоритм симплекс метода

Сформулируем алгоритм симплексного метода:

1) модель задачи приводим к каноническому виду с неотрицательными

правыми частями;

2) находим начальный опорный план (в каждом уравнении должна

быть переменная с коэффициентом единица, которая входит только в одно уравнение);

3) составляем симплексную таблицу;

4) проверяем знаки z j − c j ;

5) если все z j − c j ≤ 0 – оптимальное решение найдено, есть минимум Z;

6) если имеются z j − c j > 0 – составляем новую симплексную таблицу

и опять проверяем знаки чисел в индексной строке. Итерации продолжаем до тех пор, пока получим в индексной строке все неотрицательные числа или установим отсутствие оптимального решения задачи ( z j − c j > 0, а все числа ai′ j ≤ 0 для вектора, вводящегося в базис);

7) новую симплексную таблицу пересчитываем по правилу полных

жордановых исключений.

Замечание .Если задача задана на max, то не обязательно переходить

к нахождению min. Можно решать задачу на max, но тогда в индексной строке необходимо получить неотрицательные оценки. В базис вводят вектор с наименьшей отрицательной оценкой.

32. Выбор базиса и построение начального опорного плана при решении задачи симплекс методом.

Чтобы применить симплекс-метод с заданным базисом КЗЛП должна содержать единичную подматрицу порядка , т. е. каждое уравнение должно содержать переменную, которая входит только в одно уравнение с коэффициентом равным единице. В этом случае очевиден первоначальный опорный план (неотрицательное базисное решение системы ограничений). Для проверки полученного опорного плана на оптимальность необходимо воспользоваться критерием оптимальности, суть которого заключается в том, что для каждого вектора в системе ограничений задачи рассчитывается величина

Где:

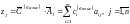
Величины называются оценками оптимальности. Величина показывает, насколько уменьшится Z, если свободную переменную увеличить на единицу. Если для известного опорного плана 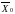при некотором фиксированном 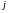разность 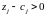, то можно построить такое множество опорных планов задачи, что для любого из них 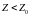, где 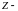значение целевой функции, соответствующее этому опорному плану.

Для проверки допустимого решения на оптимальность просматривают все 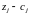. При этом могут возникнуть такие случаи:

1) если все 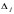<=0, то план оптимальный, т.е. имеем min Z;

2) если имеются > 0 и среди чисел , стоящих в столбце, который соответствует вектору 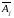, нет положительных, то целевая функция неограничена на множестве её планов

3) если имеются > 0 и среди чисел 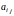имеются положительные, то можно перейти к новому опорному плану, который дает значение целевой функции, не больше предыдущего;

4) если для оптимального плана = 0 хотя бы для одной небазисной переменной и среди чисел имеются положительные, то оптимальный план не единственный. !!! Для базисного вектора всегда = 0.

Если после оценивания опорного плана на оптимальность он окажется не оптимальным, необходимо перейти к новому опорному плану путём перехода к новому базису по правилу полных жордановых исключений, которое будет описано ниже в примере.