3. Общие представления о рассеивании электронов и дырок

Один из факторов рассеивания связан с тепловыми колебаниями атомов решетки (акустическими и оптическими фононами, рис.5) [4, 10 - 12]. Эти колебания изменяют расстояние между атомами на протяжении многих периодов решетки (деформируют кристалл), а поэтому изменяют и, породившее разрешенные электронные энергетические зоны (рис. 2), расщепление атомных уровней, т. е., вызывают изменение потенциальной энергии электронов. Этот эффект принято называть рассеянием на деформационном потенциале. Расщепление уровней атомов при их сближении вызвано принципом Паули. Он состоит в том, что в заданном квантовом состоянии не может находиться более одного электрона [13 - 15]. В полярных полупроводниках, например, в GaAs, тепловые смещения заряженных атомов решетки приводят к электрической поляризации кристалла, а поэтому непосредственно влияют на движение носителей [4, 10, 11].

Отметим, что с уменьшением энергии ширины разрешенных зон уменьшаются, а ширины запрещенных зон увеличиваются, причем, чем глубже атомный уровень, тем с меньших расстояний между атомами начинается расщепление его энергии (рис. 2). Это обусловлено тем, что с увеличением глубины атомного уровня влияние внутриатомных сил возрастает по сравнению с силами межатомного взаимодействия. Ширины запрещенных зон также увеличиваются с уменьшением температуры за счет уменьшения амплитуды колебаний атомов. Последнее означает увеличение, в среднем, расстояния между атомами, а поэтому, уменьшение их взаимодействия. Расщепление атомных уровней позволяет разместить имеющиеся во всей совокупности атомов электроны и переводить их в другие квантовые состояния.

С понижением температуры всё большую роль начинает играть рассеяние на дефектах решетки, в том числе, на заряженных или нейтральных примесных атомах. Наиболее просто рассеяние на примесных атомах можно проанализировать классически [16, 17], как задачу двух тел с кулоновским взаимодействием (отталкиванием или притяжением) - в первом случае, или же с механическим столкновением - во втором. И классическое [16, 17], и квантовое [10, 11] рассмотрения показывают, что столкновения носителей с примесными атомами (без внутреннего возбуждения последних) являются квазиупругими, т. е., энергия носителей почти не меняется (но импульс может сильно изменяться). Квазиупругость рассеяния обусловлена большой массой примесного атома по сравнению с массой носителей .

Поясним это на простом примере механического столкновения двух частиц с лёгкой (light-weight) и тяжёлой (heavy-weight) массами и коллинеарными начальными импульсами и . Ось координат направим

РЗ

расщепление атомные

уровни

ЗЗ

Рис. 2. Возникновение разрешенных и запрещенных электронных энергетических зон в твердом теле в результате расщепления атомных

энергетических уровней. - расстояние между атомами, - абсолютная величина базисного вектора кристалла (равновесного расстояния между соседними атомами), РЗ – разрешенные зоны, ЗЗ – запрещенные зоны.

вдоль ( рис. 3а, b). Тогда законы сохранения энергии (10) и импульса

(11) будут описываться выражениями

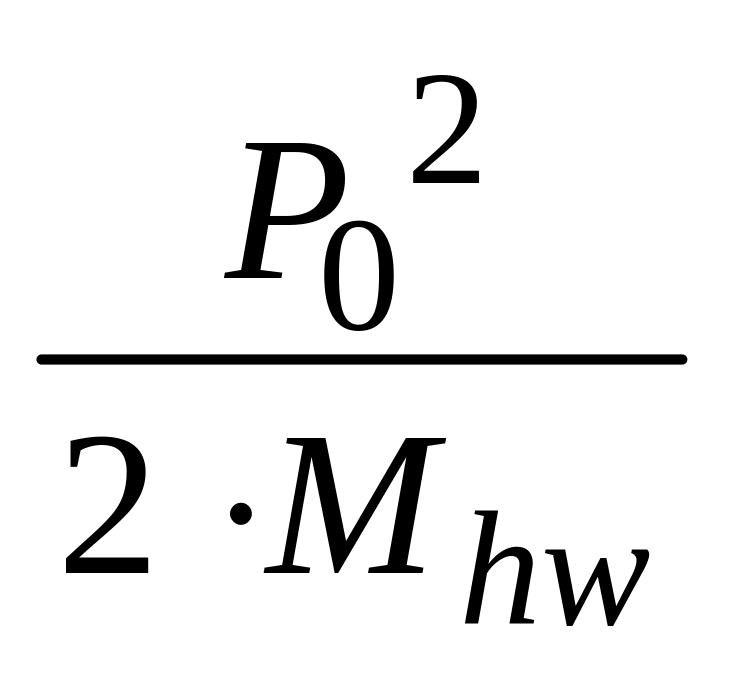(10)

(11)

где , ; в обозначении и далее верхний знак отвечает случаю

, ,

a

, ,

b

c

1

Р ис. 3. Механическое столкновение легкой и тяжелой

частиц: a - легкая частица нагоняет тяжелую; b - встречное движение частиц; с - зависимость степени упругости от отношения начальной

скорости легкой частицы к ее средне равновесной скорости .

одинаковых направлений начальных импульсов частиц, а нижний - противоположных; и - проекции импульсов легкой и тяжёлойчастиц на ось координат после столкновения.

Отметим, когда легкая частица нагоняет тяжёлую (рис. 3а), то , где , , и - начальные скорости легкой и тяжёлой частиц, соответственно. Решение системы уравнений (10) и (11) можно записать в виде

(12)

Используя (12) найдем, что относительное изменение энергии легкой час-тицы определяется выражением

, (13)

из которого видно, что значение зависит от начальных энергий (скоростей) легкой и тяжёлой частиц и . Поэтому, столкновение может оказаться сильно неупругим даже при

(14)

Для процесса лавинного размножения важны, прежде всего, близкие к средне статистическим значения энергии (скорости) и более высокие. Верхние значения равны, по порядку величины, пороговым энергиям (раздел 7) ударной генерации электронно-дырочных пар (скоростей ). Эти значения из-за малого отношения удовлетворяют неравенству

(15)

В нашей модели аналогами и являются и . Поэтому, при выполнении соотношения (15) из (13) найдем, что

, (16)

где относительное изменение средней кинетической энергии легкой частицы при тепловом равновесии (equilibrium)

, (17)

а отношение средних равновесных скоростей и частиц

= (18)

Выражения (17) и (18) следуют из равенства = = при тепловом равновесии невырожденного полупроводника, где - постоянная Больцмана. Так как  , то

 (19)

При начальных скоростях , больших , относительное изменение энергии легкой частицы , как это видно из ((16)), ещё меньше (рис.3с), чем значение .

В таблице 1 в приближении эффективной массы (4) приведены отношения для некоторых полупроводников при температуре К, где - относительное изменение после столкновения энергии легкой частицы (электрона или дырки) с начальными энергиями, равными .

Напомним, что при рассеянии на примесных атомах наряду с малым изменением энергии легкой частицы (электрона или дырки) импульс (его направление) изменяется сильно [10 - 13, 16, 17]. Это следует и из выражения (127). Рассмотренный выше пример иллюстрирует общее правило, что время релаксации (изменения) импульса обычно много меньше,

чем энергии .

Существуют, конечно, и другие механизмы рассеяния носителей. Напри-мер, электроны за счет заряда отталкивают друг друга. Такое рассеяние называют межэлектронным [10, 12, 17]. . Оно вообще не изменяет энергии электронов в целом, лишь способствуют более хаотичному движению носителей.

Материал		Ge	GaSb	Si	InP	GaAs	GaP
Eg, eV		0.66	0.72	1.12	1.33	1.42	2.26
Ei, eV	электроны	0.9	0.8	1.4	1.84	2.05	3.5
	дырки	1.3	0.79	1.6	1.65	1.81	3.7
	электроны	0.167	0.177	0.134	0.117	0.110	0.085
	дырки	0.139	0.177	0,125	0.123	0.118	0.082

Таблица 1. Степень изменения энергии легкой частицы (электрона или дырки), обладающей кинетической энергией , с тяжелой частицей (примесным атомом). Значения ширин запрещенных зон и пороговых энергий ударной ионизации взяты из литературы [1, 4, 17]/

Из-за большой напряженности электрического поля [1, 2, 4, 9] лавинный пробоя практически можно наблюдать лишь в высокоомных (невырожденных) полупроводниках (обратно смещенных - переходах). Образец с большой проводимостью просто сгорает при таком большом поле. Поэтому в дальнейшем мы ограничимся невырожденными полупроводниками. Отметим, что невырожденные полупроводники являются основой элементной базы твёрдотельной фотоэлектроники [6, 7, 18].

В отсутствие внешнего воздействия носители находятся в тепловом равновесии с решеткой. Функции энергетического распределения электронов и дырок в невырожденном полупроводнике являются Максвелл-Больцмановскими [2, 6, 10 - 12, 17], т. е.,

, (20)

Рис. 4. Схема распределения скоростей электронов по направлениям в двумерном случае в отсутствие (а) и при наличии (b) электрического поля.

причем, вследствие соотношения (2) усреднённая по направлениям ско-

рость носителей равна нулю. В изотропном образце распределение скоростей по направлениям вообще имеет форму шара (рис. 4а).

Если электрическое поле настолько слабо, что энергия, набирае- мая носителем на средней длине свободного пробега (mean free path) почти полностью теряется при столкновении, то распределение

носителей по энергии остается почти Максвелл-Больцмановским. Температура электронного газа и решетки (lattice), т. е., фононов, , с большой точностью остаются равными друг другу: = = . Однако, уже (рис. 4b). Это означает, что хаотическое движение носителей модулируется медленным дрейфом электронов против поля, а дырок - по полю. Другими словами, ансамбль носителей дрейфует в направлении, коллинеарном электрическому полю, со скоростью = . Значение много меньше средней тепловой скорости носителей и растет пропорционально . Это - диапазон полей выполнимости для однородного образца закона Ома , где - сопротивление образца, - протекающей через него ток под воздействием электрического напряжения . Дрейфовые скорости электронов и дырок записывают в виде

, (21)

где подвижности электронов и дрок представляют собой дрейфовые скорости соответствующих носителей в электрическом поле с напряженностью, равной единице. Эти подвижности характеризуют степень рассеяния импульса (скорости) носителей при их движении в электрическом поле [2, 6, 10 - 12, 17].