Вариант 30
Известны координаты четырех точек: , , и . Найти:
А. Координаты вектора , где
Б. Направляющие косинусы вектора .
В. Объем пирамиды с вершинами в данных точках.
В квадрате известны координаты вершины и уравнение диагонали
.
Найти уравнения сторон квадрата и
координаты точки пересечения диагоналей.
Написать уравнения плоскости, проходящей через точку перпендикулярно прямой .
Вычислить расстояние от точки до прямой , проходящей через точки и .
Вариант 31
Даны три вектора: , и . Найти:
А. Координаты вектора , где
Б. Площадь треугольника, построенного на векторах и .
В. Объем пирамиды, построенной на векторах , и .
Даны уравнения двух сторон ромба:
,
и уравнения одной из его диагоналей
.
Составить уравнения других сторон
ромба.
Составить параметрические уравнения прямой, проходящей через точку перпендикулярно плоскости
.
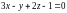Найти угол между прямой и прямой , проходящей через точку параллельно двум плоскостям
и
.
Вариант 32
Даны координаты четырех точек: , , и . Найти:
А. Координаты вектора , где
Б. Угол между вектором и гранью, в которой лежат векторы и .
В. Объем параллелепипеда, построенного на векторах , , .
В прямоугольнике
заданы уравнения двух сторон
,
и его вершина
.
Составить уравнения других сторон
прямоугольника и найти расстояние от
вершины
до диагонали, не проходящей через эту
вершину.
Определить взаимное расположение прямой и плоскости
.
Найти проекцию точки на плоскость, проходящую через прямые и
Вариант 33
Даны три вектора: , , . Найти:
А. Координаты вектора , где
Б. Направляющие косинусы вектора .
В. Высоту параллелепипеда, построенного на данных векторах, проведенную к грани векторов и .
Даны точки , , . Отрезок
разделен точкой
в
отношении
.
Найти расстояние от точки
до прямой
,
записать уравнение высоты треугольника
,
проведенной к стороне
.
Проверить, можно ли провести плоскость, через следующие четыре точки: , , , .
Плоскость проходит через прямую перпендикулярно плоскости
.
Прямая
проходит через точку
перпендикулярно
прямым
и
.
Найти точку пересечения плоскости
и прямой
.
Вариант 34
Даны координаты четырех точек: , , и . Найти:
А. Координаты вектора , где
Б.
Угол между вектором
и плоскостью, в которой лежат векторы
и
.
В. Объем пирамиды с вершинами в данных точках.
На прямой
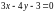найти точку, отстоящую от прямой
на расстоянии трех единиц (два решения).
Написать уравнение прямой, проходящей
через найденную точку, перпендикулярно
второй прямой.
Составить параметрические уравнения прямой, проходящей через начало координат параллельно прямой
Через прямую провести плоскость перпендикулярно плоскости:
.
Найти угол между плоскостью
и плоскостью
.