Вариант 20
Известны координаты четырех точек , , , . Найти:
А. Координаты вектора , где
Б. Единичный вектор, коллинеарный вектору и сонаправленный с ним.
В.
Объем пирамиды, построенной на векторах
,
и
.
Треугольник
задан координатами своих вершин
,
,
.
Найти расстояние от середины стороны
до высоты, опущенной из вершины
.
Написать канонические уравнения прямой, образованной пересечением плоскости
с координатной плоскостью
.
Найти уравнение плоскости , проходящей через точку перпендикулярно двум плоскостям
,
.
Вычислить
угол между плоскостью
и осью
.
Вариант 21
Известны координаты четырех точек , , , . Найти:
А.
Координаты вектора
,
где
Б. Направляющие косинусы вектора .
В. Высоту параллелепипеда, опущенную на грань векторов и
Найти координаты вершин ромба, если известны уравнения его сторон
,
и уравнение одной из его диагоналей
.
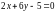Составить параметрические уравнения прямой, образованной пересечением плоскости
с координатной плоскостью
.
Прямая , проходит через точку параллельно прямой
Найти
координаты точки пересечения прямой
и
плоскости
.
Вариант 22
Даны три вектора , , . Найти:
А. Координаты вектора , где
Б. Направляющие косинусы вектора .
В. Высоту параллелепипеда, опущенную на грань векторов и
Найти расстояние от точки до прямой, проведенной перпендикулярно к отрезку
через его середину:
,
.
Составить канонические уравнения прямой, проходящей через точку параллельно прямой .
Написать уравнение плоскости, проходящей через прямую параллельно прямой , которая проходит через точку перпендикулярно плоскости
.
Вариант 23
Известны координаты четырех точек , , , . Найти:
А. Координаты вектора , где
Б. Объем пирамиды, с вершинами в данных точках.
В. Угол между вектором и гранью, в которой лежат векторы и .
В треугольнике :
,
,
.
Найти расстояние от вершины
до прямой, проходящей через вершину
,
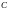параллельно медиане
.
Записать параметрические уравнения прямой, проходящей через точку параллельно оси
.
Найти проекцию точки на прямую, проходящую через точки и .
Вариант 24
Известны три вектора , , . Найти:
А. Координаты вектора , где
Б. Объем параллелепипеда, построенного на данных векторах.
В. Проекцию вектора на направление вектора .
В треугольнике известны координаты вершин , и точка пересечения его высот . Найти длину высоты .
Написать уравнения плоскости в отрезках, проходящей через точку , перпендикулярно прямой .
Найти угол между прямой , проходящей через точку параллельно прямой и плоскостью , проходящей через точку
параллельно
прямым
и
.