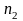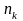Элементы математической статистики Предмет математической статистики

В основе научных знаний лежат наблюдения за изучаемыми объектами и процессами, присущими данным объектам. Однако, ясно, что единичное наблюдение вряд ли позволит сразу установить свойства наблюдаемого объкта. Поэтому для установления свойств и связей изучаемого объекта его приходится наблюдать многократно, а затем результаты наблюдений обрабатывать и лишь после этого делать выводы.

В математической статистике изучаются случайные величины и системы случайных величин при помощи наблюдений. В связи с этим в математической статистике (которая достаточно долго развивалась независимо от теории вероятностей) случайные величины принято называть наблюдаемыми признаками.

Первичная обработка результатов измерений.

Пусть рассматривается некоторый наблюдаемый признак Х. Назовем генеральной совокупностью наблюдаемого признака Х множество значений, которые может принимать этот наблюдаемый признак.

Набор значений 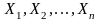, являющихся результатами наблюдений (измерений) наблюдаемого признака Х, назовем выборкой объема п из генеральной совокупности.

Отметим, что на выборку можно смотреть с двух точек зрения:

1. -результаты измерений (конкретные числа),

2. - совокупность п случайных величин, имеющих такие же распределения как и наблюдаемый признак.

Разумеется, первой точки зрения на выборку придерживаются после проведения измерений, а второй – до проведения измерений.

В этом пункте мы будем рассматривать выборку как результаты наблюдений. Как правило, объем выборки весьма велик и это мешает увидеть закономерности, присущие наблюдаемому признаку. В связи с этим возникает задача о выборе сравнительно небольшого числа представителей выборки так, чтобы были сохранены основные закономерности, описываемые исходной выборкой. Процедура решения

этой задачи называется первичной обработкой результатов измерений. Первичная обработка проводится по-разному в зависимости от типа наблюдаемого признака.

1. Ранжирование.

Пусть наблюдаемый признак Х является дискретной СВ. В этом случае, как известно, генеральная совокупность представляет собой не более чем счетное множество. В таком случае, всякая выборка есть конечное подмножество этого множества. Под ранжированием понимают расположение в порядке возрастания значений, упомянутых в выборке, с указанием количества повторов каждого значения.

Поясним сказанное примером.

Пример. Пусть Х – количество сбоев станка в течении смены. В результате проведения наблюдений получены следующие данные:

5,1,3,2,4,1,2,3,4,5,3,2,2,1,2,5,4,4,4,3,1,2,3,4,5. Требуется провести первичную обработку результатов измерений.

В данном случае, очевидно, что наблюдаемый признак является ДСВ, поэтому первичная обработка есть ранжирование:

Х	1	2	3	4	5
	4	6	5	6	4

Значения 1,2,3,4,5, встречающиеся в приведенной таблице, называют вариантами, числа 4,6,5,6,4 – их частотами соответственно, а саму таблицу - вариационным рядом частот.

Отметим, что сумма частот совпадает с объемом выборки: 4+6+5+6+4=25.

Иногда вместо вариационного ряда частот используют вариационный ряд относительных частот, который отличается от вариационного ряда частот тем, что вместо частот используются относительные частоты 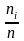. Ясно, что сумма относительных частот обязательно равна 1: .

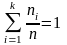В приведенном выше примере вариационный ряд относительных частот имеет вид:

Х	1	2	3	4	5
	0,16	0,24	0.20	0,24	0,16

2. Интервальная обработка выборки.

В этом пункте мы рассматриваем случай, когда генеральная совокупность не является дискретным множеством. Нашей целью является построение вариационных рядов, аналогичных рассмотренным выше. Достигается поставленная цель при помощи, описываемого ниже эмпирического алгоритма, называемого интервальной обработкой выборки.

По выборке объема п строят, так называемый интервальный ряд частот:

Х			………………
			………………

где а

При этом число интервалов расчитывается по эмпирической формуле Стерджеса , шаг h определяется по формуле , а через обозначают число наблюдений, попавших в интервал . В качестве рекомендуют выбирать .

После построения интервального ряда частот вариационный ряд частот получают из него, заменяя каждый из интервалов его одним представителем. Как правило, в качестве представителя интервала берут его середину.

Пример. Построить вариационный ряд частот и относительных частот по результатам измерений:

2,3; 2,5; 2,7; 2,35; 2,71; 2,32; 2,36; 2,44; 2,61; 2,67; 2,83; 2,86; 3,01; 3,12; 3,14; 2,61;2,49; 2,57; 2,52; 2,54; 3,03; 3,05.

Очевидно, в рассматриваемом случае п =25; , поэтому

.

Руководствуясь изложенными выше соображениями, строим интервальный ряд частот:

Х	[2,2; 2,4)	[2,4; 2,6)	[2,6; 2,8)	[2,8; 3,0)	[3,0; 3,2)	[3,2; 3,4]
	4	6	5	2	6	2

Заменяя интервалы их серединами, получаем вариационный ряд частот, а затем вариационный ряд относительных частот:

Х	2,3	2,5	2,7	2,9	3,1	3,3
	4	6	5	2	6	2

Х	2,3	2,5	2,7	2,9	3,1	3,3
	0,16	0,24	0,2	0,08	0,24	0,08

Всюду ниже мы считаем, что первичная обработка результатов измерений произведена и выборка представлена в виде вариационного ряда частот или относительных частот.