§40. Гіпотеза про рівність центрів розподілу двох нормально розподілених генеральних ознак
Припустимо,
що ознаки двох генеральних сукупностей
і
незалежні і мають нормальний закон
розподілу. Необхідно за даними вибірок
і
перевірити наступну гіпотезу:
.
По-перше, розглянемо розв’язання цієї задачі за умови, що відомі дисперсії
.
За статистичний критерій береться випадкова величина
,
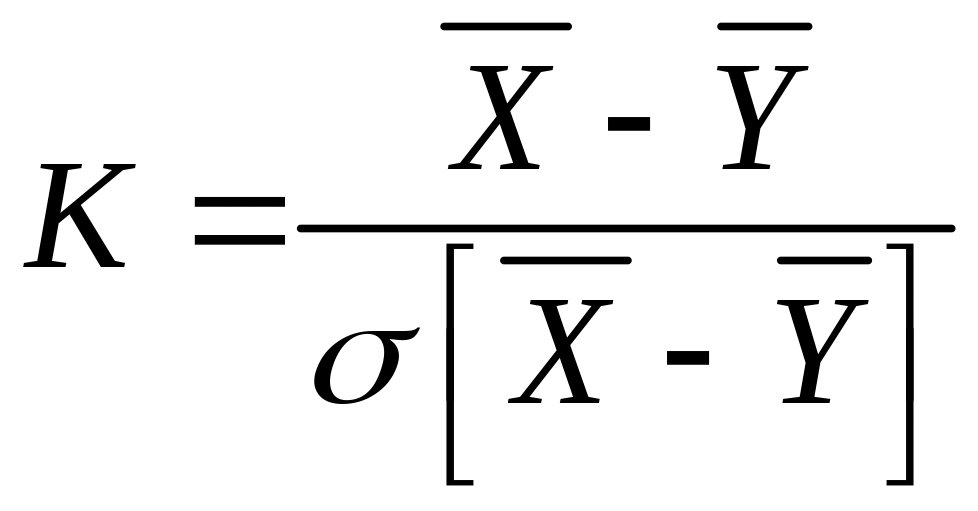(40.1)
яка
розподіляється згідно до нормального
закону при
.
За властивостями дисперсії
.
Тоді
і статистичний критерій (40.1) набирає вигляд
.
(40.2)
Критичні точки визначають згідно рівності
,
(40.3)
де – рівень значущості критерію.
Оскільки
,
то
є коренем рівняння
.
Гіпотеза
приймається за умови, що обчислене після
здійснення вибірок статистичне значення
критерію
.
У випадку,
коли немає інформації стосовно генеральних
дисперсій
і
,
то замість них розглядаються вибіркові
виправлені дисперсії
.
З метою
спрощення будемо вважати, що
.
Оскільки дисперсії ознак і рівні, то незміщеною її оцінкою за результатами обох вибірок є величина
.
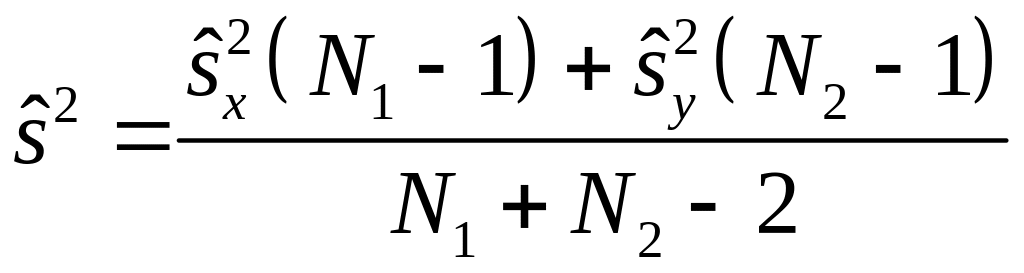(40.4)
З умов незміщенності випливає
.
За критерій обирається наступна величина:
.
(40.5)
Якщо
гіпотеза
є вірною, то
,
а
.
З урахуванням останніх формул (40.5) переписується у вигляді:
.
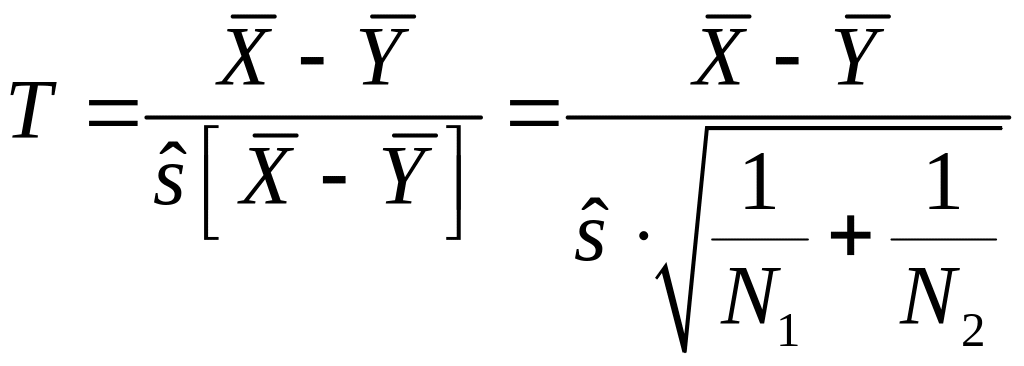Випадкова
величина
,
що визначається формулами (40.5), (40.6) має
–розподіл
Ст’юдента з
степенями свободи. Це використовується
для знаходження критичних точок з умови
при заданому рівні значущості.
§41. Перевірка гіпотез про закон розподілу. Критерій згоди Пірсона. Критерій Колмогорова
В попередніх параграфах розглядались питання перевірки параметричних гіпотез, тобто гіпотез відносно параметрів розподілу. Розглянемо критерії для перевірки непараметричних гіпотез – гіпотез відносно закону розподілу.
Нехай
– ознака генеральної сукупності, що
досліджується і потрібно перевірити
гіпотезу
– функція розподілу
.
Вважаємо, що за результатами вибірки об’єму отримано інтервальний розподіл:
де
.
За
допомогою висунутої за гіпотезою функції
розподілу
знаходяться теоретичні ймовірності
.
Відповідно до критерію згоди Пірсона розглядається випадкова величина
.
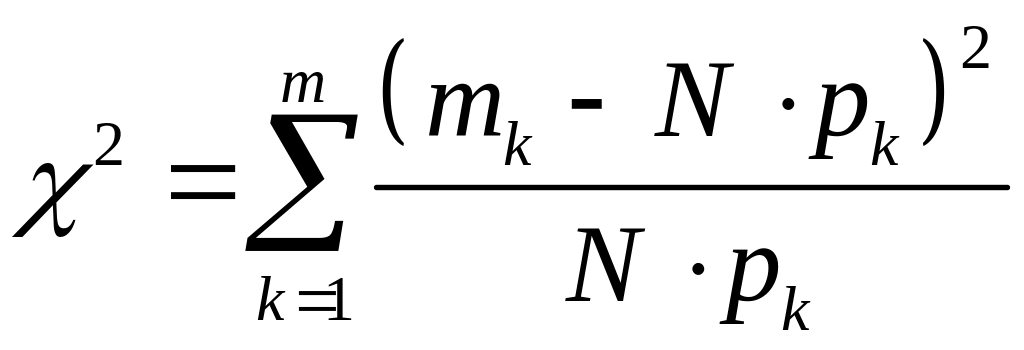(41.1)
Випадкова
величина
(41.1) розподілена за законом
з степенями вільності
,
де
– число параметрів розподілу, що входять
у
.
Для
застосування критерію Пірсона задається
рівень значущості
гіпотези
і визначається критичне значення
з рівності
.
(41.2)
Після чого за результатами вибірки обчислюється вибіркове значення за формулою (41.1).
Тоді якщо:
1.
,
то гіпотеза
приймається;
2.
,
то гіпотеза
відхиляється.
Нехай
– емпірична функція розподілу, знайдена
за результатами вибірки. Відповідно
критерію Колмогорова розглядається
випадкова величина
.
(41.3)
Колмогоровим
знайдено граничну функцію розподілу
випадкової величини
,
яка називається функцією
Колмогорова
і дорівнює
.
(41.4)
Якщо об’єм вибірки досить великий, то можна вважати, що
.
При
практичному застосуванні критерію
Колмогорова будуються графіки емпіричної
і гіпотетичної
функцій розподілу і знаходиться вибіркове
за формулою (41.3). За допомогою (41.4)
обчислюється ймовірність
.
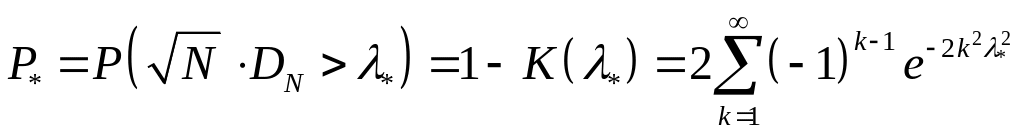Якщо:
гіпотеза
приймається;
гіпотеза
відхиляється.