Глава VI інтервальні статистичні оцінки. Статистичні гіпотези і критерії узгодження

§37. Інтервальні статистичні оцінки. Довірчий інтервал і його надійність. Побудова довірчих інтервалів для параметрів нормального закону розподілу

Вибіркова оцінка параметра розподілу генеральної сукупності сама є випадковою величиною з певним законом розподілу. Тому наближена заміна може привести до істотних похибок особливо при малому об’ємі вибірки. У випадку, коли вибіркова оцінка не надійна, використовують інтервальні оцінки параметрів розподілу.

Якщо при реалізації вибірки встановлюють два числа такі, що , то кажуть, що числа і утворюють інтервальну оцінку параметра розподілу . Але усі оцінки і , знайдені за даними вибірки, самі є випадковими величинами. Тому й подія, яка полягає в тому, що буде мати місце нерівність , теж є випадковою і має певну ймовірність здійснення.

Інтервал називається довірчим інтервалом з надійністю для оцінювання параметра розподілу , якщо виконується рівність

. (37.1)

Як можна бачити з означення, число у правій частині рівності (37.1) називається надійністю довірчого інтервалу .

Нехай відомо, що ознака генеральної сукупності розподілена за нормальним законом з . Реалізована вибірка об’єму значень цієї ознаки . Необхідно за даними вибірки здійснити інтервальні оцінки параметрів розподілу і з надійністю .

Почнемо з побудови довірчого інтервалу за умови, що відома дисперсія . Візьмемо обчислене за даними здійсненої вибірки вибіркове середнє і визначимо число так, що виконується рівність

. (37.2)

Вже було показано, що при нормальному законі розподілу генеральної сукупності теж розподілена за нормальним законом з параметрами розподілу . Тому для обчислення ймовірності у (37.2) можна скористатись формулою (21.4)

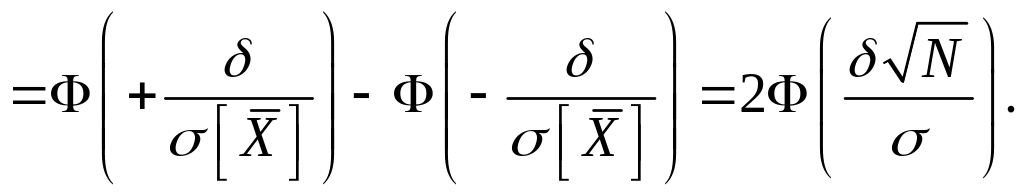
Після підстановки результатів обчислення у (37.2) маємо

.

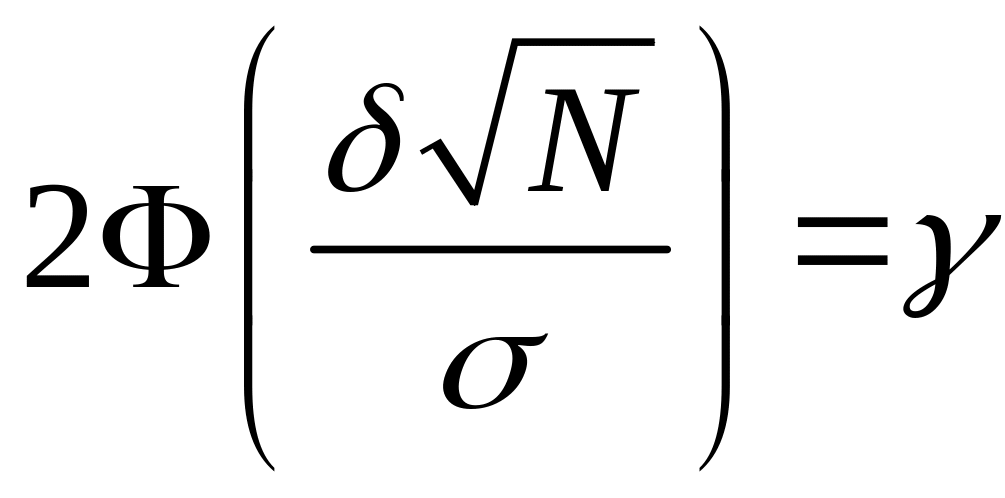Розглянемо рівняння

.

і будемо вважати, що – його розв’язок, який буде єдиним, оскільки зростаюча функція. Оберемо число так, щоб

.

Тоді є вірною рівність

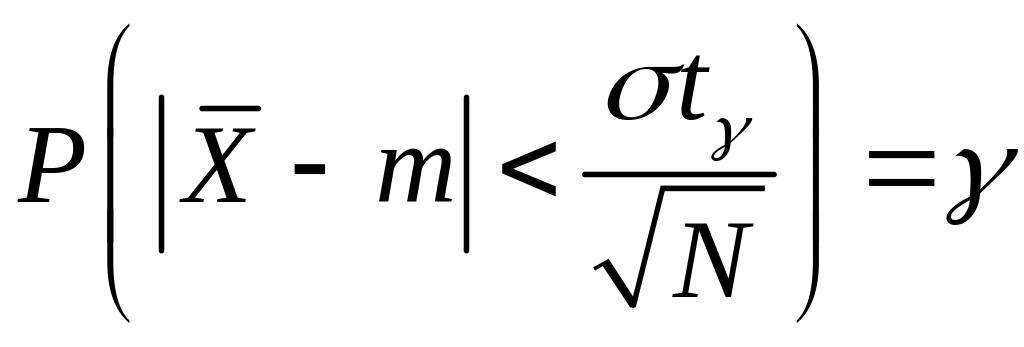
Але остання рівність еквівалентна наступній

. (37.3)

Рівність (37.3) згідно з (37.1) означає, що інтервал

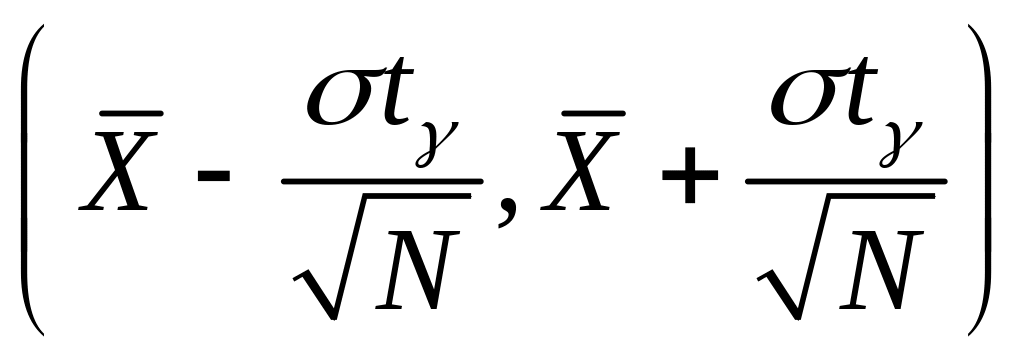
є довірчим інтервалом для математичного сподівання з надійністю .

Отриманий довірчий інтервал має той недолік, що ним можливо користуватися у випадку, коли є досить точна вибіркова оцінка для дисперсії . Розглянемо проблему побудови довірчого інтервалу для математичного сподівання при невідомому значенні дисперсії. Для цього необхідно скористатися тим, що випадкова величина

, (37.4)

як було відмічено у §34, розподілена за законом Ст’юдента з ступенями свободи, де – вибіркове середнє, а – незміщена вибіркова дисперсія

Розглянемо рівність (37.2), в яку підставимо знайдене з (37.4) значення:

.

Отримаємо:

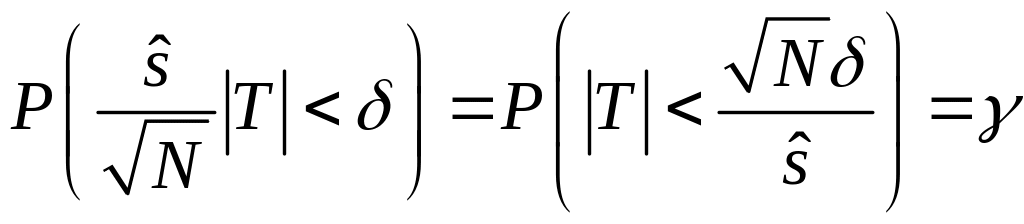. (37.5)

Нехай густина розподілу Ст’юдента з ступенями свободи. Тоді маємо

. (37.6)

Позначимо через розв’язок рівняння

. (37.7)

Значення може бути наближено знайдено за допомогою відповідних таблиць.

Визначимо величину з умови

.

Тоді є вірною наступна рівність, що випливає (37.2)

.

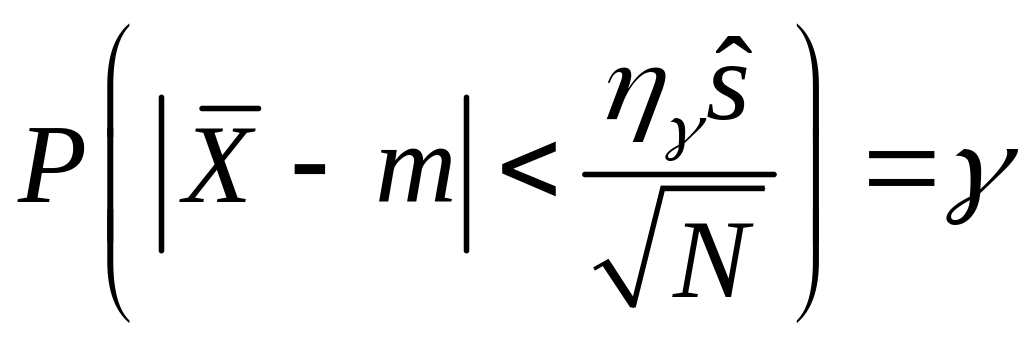Або

. (37.8)

Рівність (37.8) означає, що є довірчим інтервалом для математичного сподівання з надійністю .

Розглянемо питання побудови довірчого інтервалу для дисперсії . Припустимо, що за даними вибірки обчислено незміщену вибіркову дисперсію . Визначимо числа і з умови

. (37.9)

Для цього скористаємось законом розподілу випадкової величини ( –розподілу з ступенями свободи).

.

Тепер, якщо врахувати

,

(37.9) перепишемо у вигляді:

або

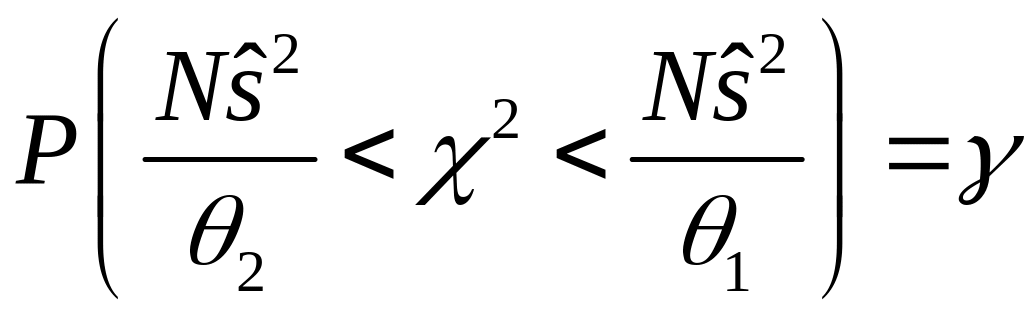. (37.10)

Нехай – функція –розподілу з степенями свободи, тоді з (37.10) знайдемо

.

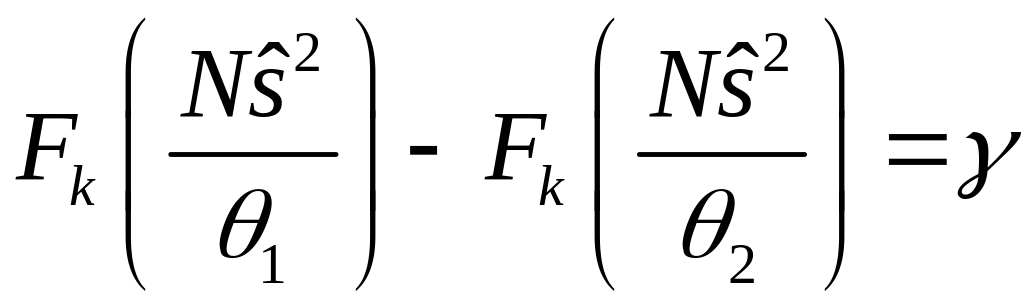Нехай числа і такі, що виконуються рівності

.

Наближені значення , можуть бути знайдені за допомогою відповідної таблиці. Оберемо так, щоб виконувались рівності

,

звідки

.

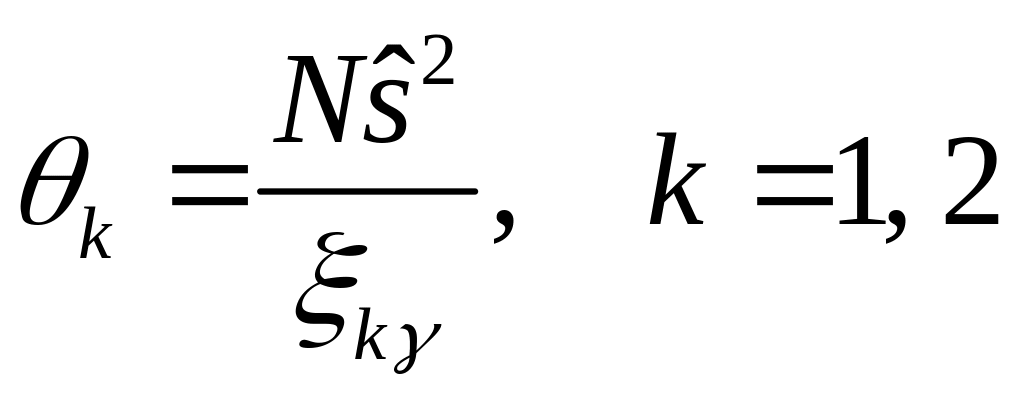Тепер, якщо знайдені підставити у (37.9), то рівність

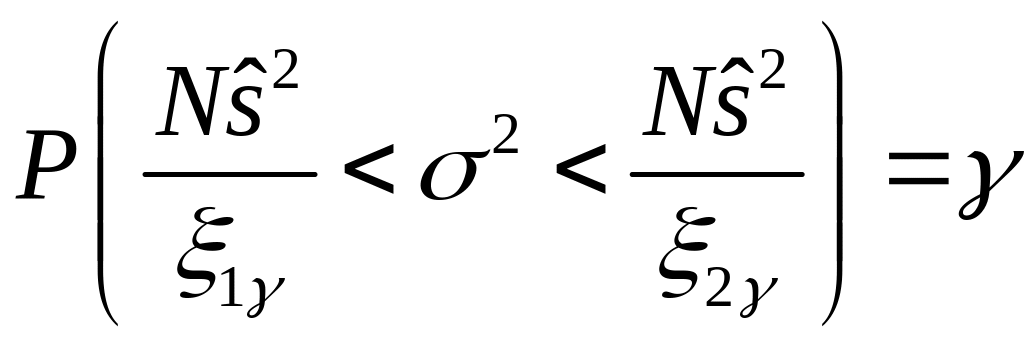
є вірною. Останнє означає, що інтервал є довірчим інтервалом для дисперсії з надійністю .