§ 18. Біноміальний закон розподілу

Біноміальним називається закон розподілу випадкової величини , яка є числом появи події у незалежних випробуваннях, причому в кожному з них ймовірність появи події однакова і дорівнює .

Можливими значеннями цієї випадкової величини є числа . Ймовірність кожного з цих значень знаходиться за формулою Бернуллі і дорівнює:

. (18.1)

Тепер можемо записати ряд розподілу:

	0	1	2	...
				...

Зауважимо, що має виконуватись рівність

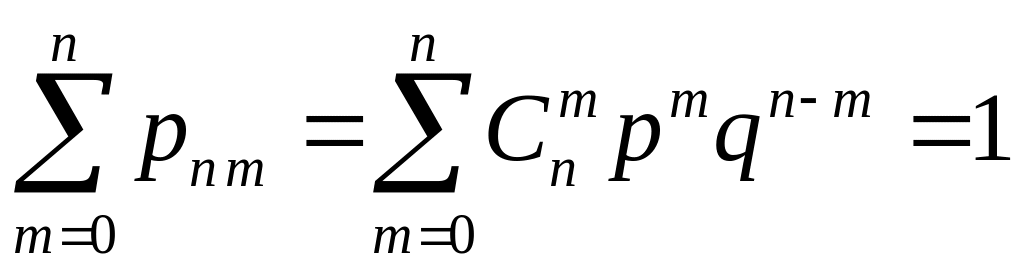. (18.2)

Знайдемо основні числові характеристики біноміального закону розподілу. За формулою (15.2) для математичного сподівання знаходимо

. (18.3)

Значення суми, що знаходиться у формулі (18.3) можна підрахувати. Для цього, по-перше, скористаємось формулою бінома Ньютона (дивись, наприклад, [3], [12]) .

.

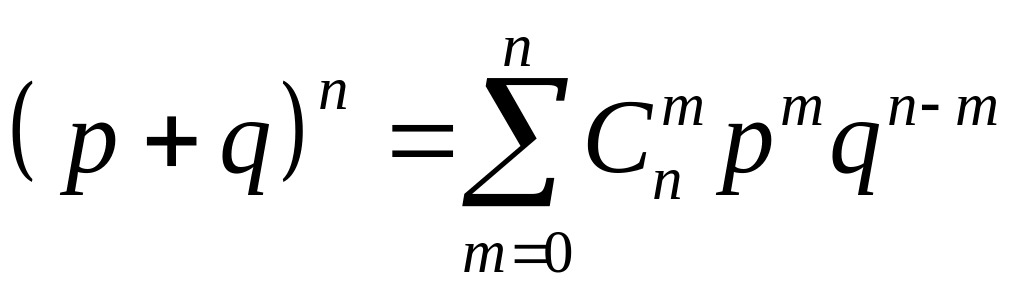Продиференціюємо цю рівність за :

. (18.4)

Після множення обох частин (18.4) на знаходимо

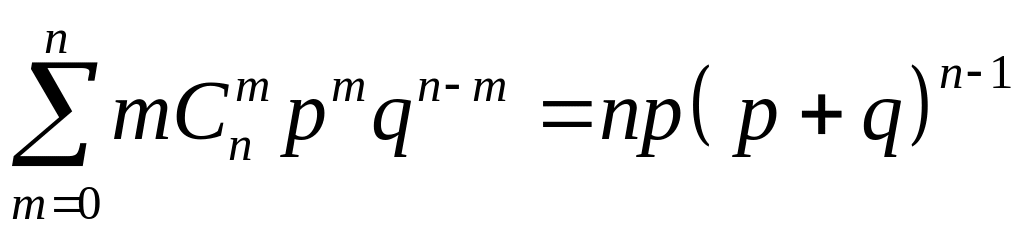
Тепер з (18.3) знаходимо

.

Оскільки , то остаточно маємо

. (18.5)

Для підрахунку дисперсії скористаємось формулою (16.6), для чого попередньо знайдемо

. (18.6)

Щоб підрахувати цю суму знову ж таки продиференціюємо за формулу (18.4)

.

Отриману рівність помножимо на

.

З урахуванням того, що , знаходимо

.

Тоді

.

Для дисперсії, згідно з (16.6), знаходимо

.

Таким чином, для випадкової величини, розподіленою за біноміальним законом

. (18.7)

§ 19. Рівномірний закон розподілу

Неперервна випадкова величина називається рівномірно розподіленою на , якщо її густина розподілу має вигляд

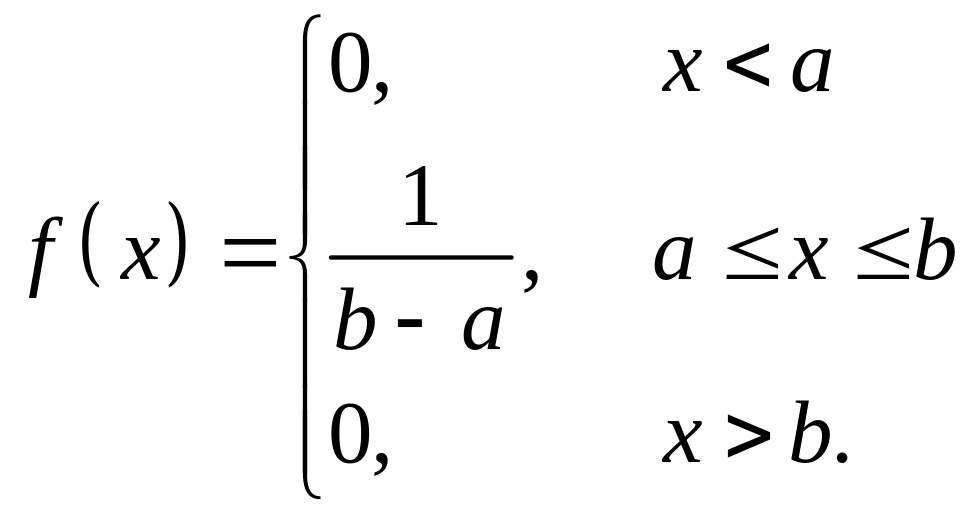(19.1)

Графік густини розподілу (диференціальна крива розподілу) має вигляд

Рис. 8

Знайдемо вираз для функції розподілу. Очевидно, що

.

Коли

.

При .

Таким чином, маємо:

(19.2)

Графік функції розподілу (інтегральна крива розподілу) має вигляд:

Рис. 9

Визначимо ймовірність того, що значення випадкової величини, розподіленої рівномірно, належить проміжку . Користуючись формулою (12.2), знаходимо:

.

Основні характеристики рівномірно розподіленої випадкової величини. Знаходимо математичне сподівання за формулою (15.3):

.

Після очевидного спрощення маємо:

. (19.3)

Щоб знайти дисперсію за формулою (16.6) спочатку обчислимо

.

Після спрощення знаходимо:

.

Тепер за допомогою (16.6), (19.3) можна обчислити дисперсію

. (19.4)

Середнє квадратичне відхилення рівномірно розподіленої випадкової величини дорівнює:

. (19.5)