Глава III числові характеристики одновимірних випадкових величин і приклади основних законів розподілу
§ 15. Математичне сподівання одновимірної випадкової величини і його властивості
При розв’язанні практичних задач немає необхідності, а у випадку неперервної величини неможливо знати усі можливі значення випадкової величини. Зручніше використовувати деякі числові величини, які дають інформацію про її значення. Такі величини називають числовими характеристиками випадкової величини. Головними з них є математичне сподівання, дисперсія, середнє квадратичне відхилення, моменти різних порядків.
Нехай
є одновимірна дискретна величина
,
яка визначається наступним рядом
розподілу:
-
...
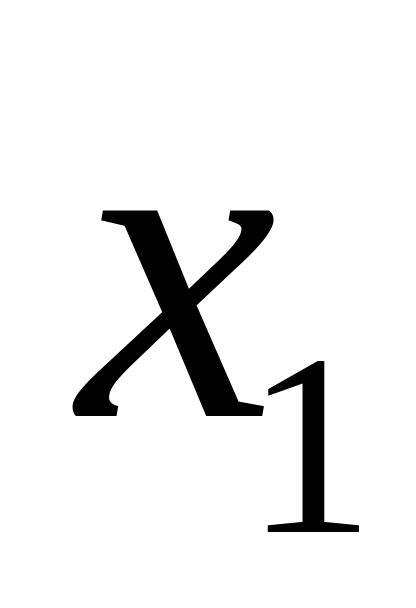
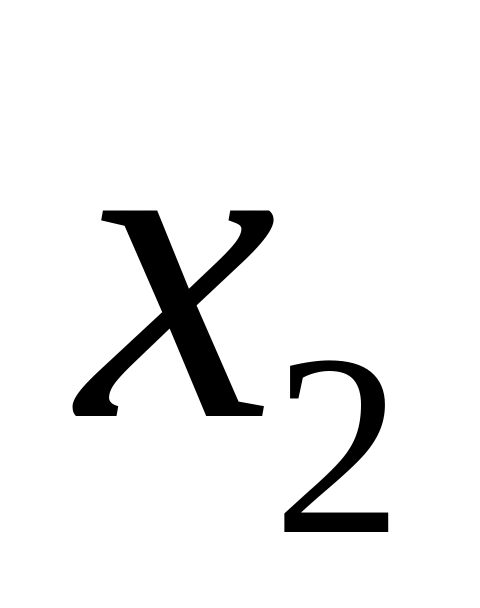
(15.1)
...
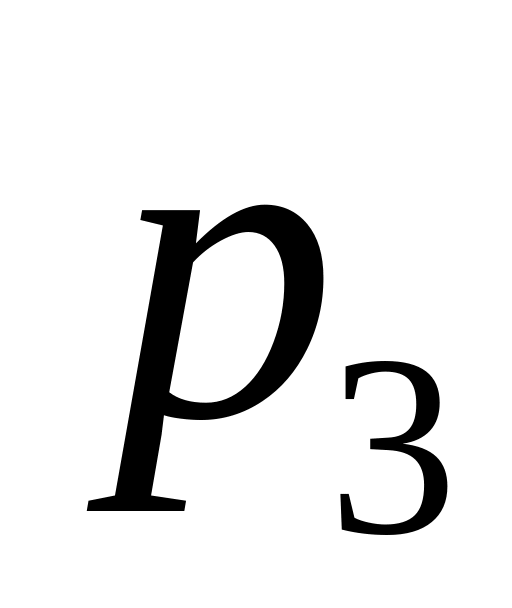
Математичним сподіванням одновимірної випадкової величини називається сума добутків усіх її можливих значень на їх ймовірності:
.
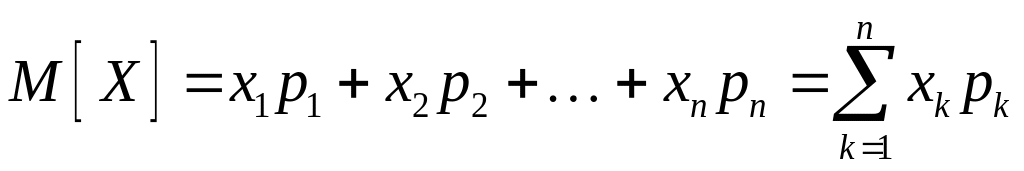(15.2)
Нехай
тепер
– неперервна випадкова величина з
густиною розподілу
.
Математичним
сподіванням неперервної випадкової
величини
називається інтеграл
.
(15.3)
З формули (15.2) можна бачити, що математичне сподівання є зваженим за ймовірностями середнім значенням випадкової величини.
Розглянемо головні властивості математичного сподівання.
1.
Математичне
сподівання сталої (невипадкової) величини
дорівнює самій цій величині
.
(15.4)
2. Математичне сподівання суми двох випадкових величин дорівнює сумі їх математичних сподівань
.
(15.5)
Дійсно,
нехай закон розподілу випадкової
величини
задається законом розподілу (15.1), а
величина
має наступний закон розподілу:
-
...
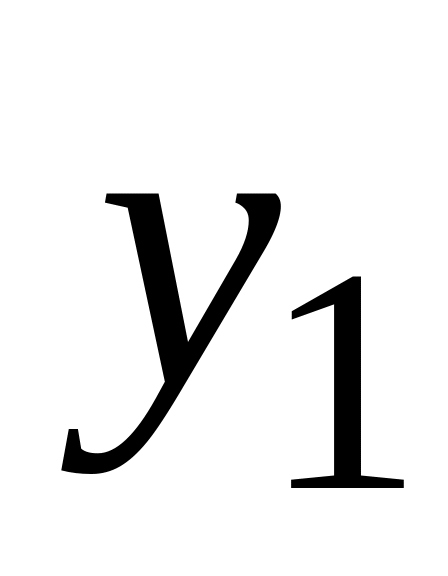
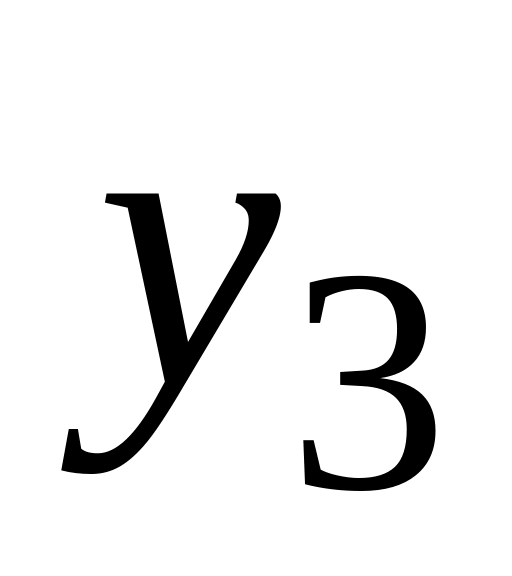
(15.6)
...
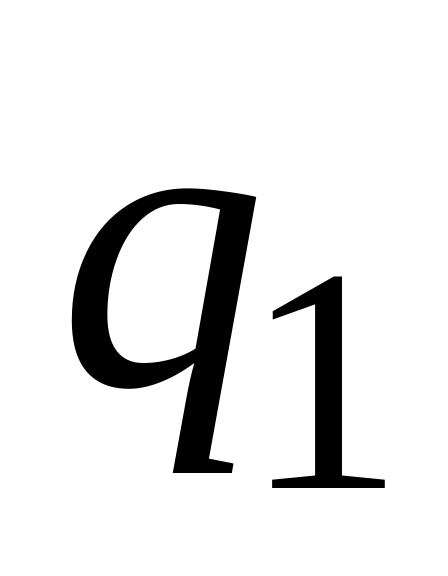
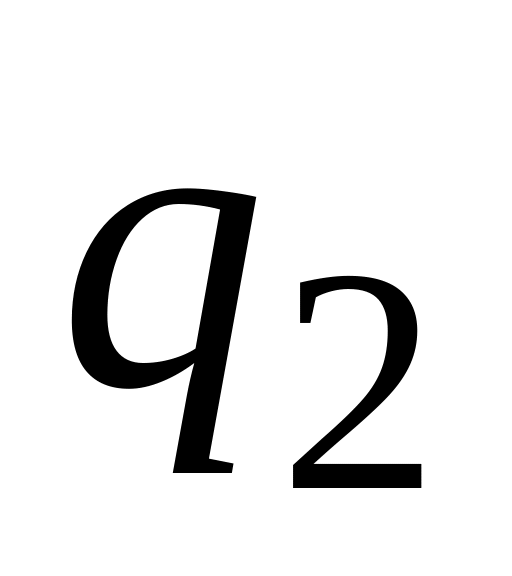
Тоді згідно з означенням:
.
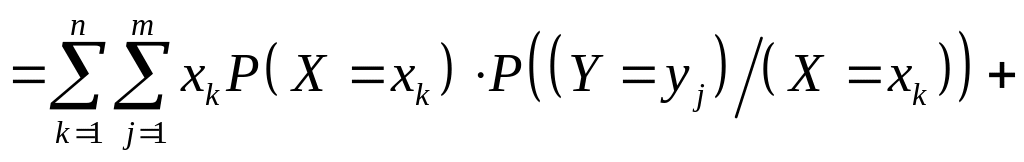
Оскільки
події
за умови
і
за умови
– несумісні і єдиноможливі, то
;
.
Тому
.
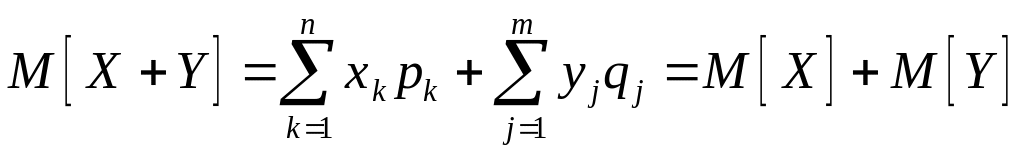Формулу (15.5) можна легко узагальнити на довільну скінчену кількість випадкових величин:
.
(15.7)
3. Для будь-якої сталої
.
(15.8)
Щоб
сформулювати наступну властивість
необхідно ввести поняття незалежних
випадкових величин. Випадкові
величини
називаються взаємно
незалежними,
якщо закон розподілу кожної з них не
залежить від того які значення приймають
інші величини.
4. Математичне сподівання добутку двох незалежних випадкових величин дорівнює добутку їх математичних сподівань
.
(15.9)
Дійсно, для незалежних дискретних величин з законами розподілу (15.1), (15.6) маємо:
.