Глава IV залежність і незалежність випадкових величин. Характеристики двовимірних розподілів

§ 25. Залежні та незалежні випадкові величини. Умовні закони розподілу

Нехай є двовимірна випадкова величина . Випадкові величини і називаються незалежними, якщо закон розподілу однієї з них не залежить від того, яке значення набула інша. У протилежному випадку випадкові величини є залежними. Оскільки у випадку залежності випадкових величин закон розподілу залежить від того, яке значення набула інша величина, то доцільно ввести поняття умовного закону розподілу.

Умовним законом розподілу випадкової величини називається її закон розподілу, визначений за умови, що інша випадкова величина прийняла значення .

Умовний закон розподілу можна задавати як умовною функцією розподілу , так і умовною густиною розподілу . Обмежимося випадком, коли та – неперервні випадкові величини.

Розглянемо елементарний прямокутник, що прилягає до точки зі сторонами і відповідно

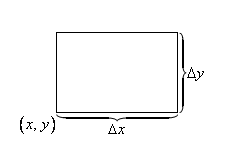
Рис. 11

Тоді під умовними густинами розподілу розуміються границі

,

. (25.1)

Покажемо як пов’язані густини двовимірної випадкової величини з густинами розподілу кожної із складових і умовними густинами. Згідно з теоремою про ймовірність добутку подій маємо:

.

Розділимо обидві частини рівності на добуток і спрямуємо . Тоді згідно з (12.1), (13.1), (25.1) знайдемо

. (25.2)

Аналогічно

. (25.3)

У формулах (25.2) і (25.3) – густина розподілу , – густина розподілу , – двовимірна густина розподілу, – умовні густини розподілу.

Таким чином має місце наступна теорема.

Теорема (множення законів розподілу). Густина розподілу системи двох випадкових величин дорівнює добутку густини розподілу однієї з величин, що складає систему, на умовну густину розподілу іншої випадкової величини.

Формули (25.2) і (25.3) дозволяють обчислити умовні густини розподілу через безумовні:

. (25.4)

Завдяки (13.5) формули (25.4) можуть бути ще переписані наступним чином:

. (25.5)

Теорема. Нехай випадкові величини і незалежні. Тоді густина розподілу системи випадкових величин дорівнює добутку густин розподілу цих величин.

Дійсно, якщо і незалежні, то і . Тоді з (25.2) і (25.3) маємо

. (25.6)

Умова (25.6) є необхідною і достатньою умовою незалежності двох неперервних випадкових величин, закон розподілу яких визначається густиною.

§ 26. Числові характеристики системи двох випадкових величин. Умовні математичні сподівання і дисперсія

Числовими характеристиками двовимірної випадкової величини є начальні і центральні моменти.

Початковим моментом порядку двовимірної випадкової величини називається математичне сподівання добутку

.

Якщо випадкова величина дискретна і має закон розподілу (10.2), то

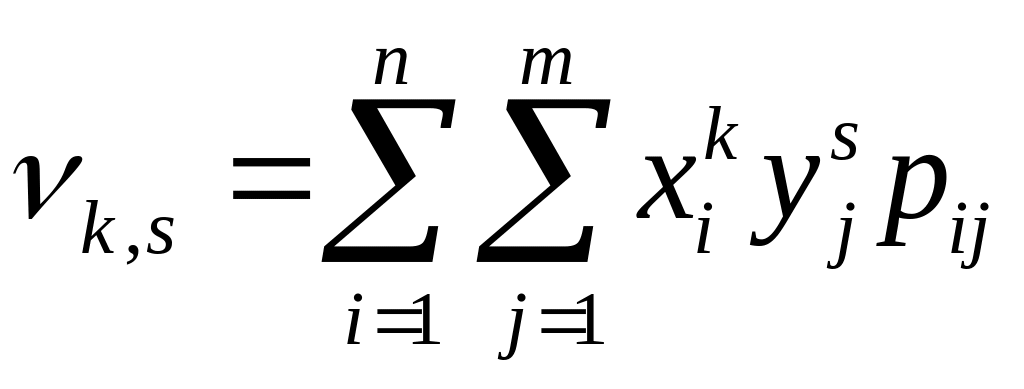. (26.1)

Якщо – неперервна випадкова величина і має густину розподілу , то

. (26.2)

Очевидно, що

.

Центральним моментом порядку називається математичне сподівання -го і -го степеня відповідних центрованих величин і :

.

Якщо величини є відповідно дискретними або неперервними, ці моменти обчислюються за формулами:

,

. (26.4)

Очевидно, що

.

Якщо величини , що складають двовимірну випадкову величину, залежні, то важливими числовими характеристиками є умовне математичне сподівання і умовна дисперсія.

Нехай двовимірна величина є дискретною і має закон розподілу (10.2). Тоді умовним математичним сподіванням випадкової величини за умови називається наступна сума

. (26.5)

У випадку неперервних випадкових величин умовним математичним сподіванням називається інтеграл

. (26.6)

Відповідно визначається і умовна дисперсія

,

. (26.7)