§33. Метод максимальної правдоподібності статистичного оцінювання параметрів розподілу

Припустимо, що ознака генеральної сукупності характеризується параметрами і має густину розподілу . Нехай реалізовано вибірку значень ознаки об’єму : . За даними цієї вибірки будується функція правдоподібності

. (33.1)

Статистичними оцінками параметрів розподілу є значення , при яких функція правдоподібності набуває максимуму.

На практиці від функції (33.1) зручніше перейти до її логарифма (логарифмічної функції правдоподібності)

. (33.2)

Якщо функція (33.2) є диференційовною, то оцінки , згідно з необхідною умовою екстремуму, слід шукати серед розв’язків системи рівнянь:

. (33.3)

Реалізуємо цей метод, коли ознака розподілена за нормальним законом з густиною розподілу

.

У цьому випадку ознака характеризується двома основними параметрами: математичним сподіванням і середнім квадратичним відхиленням . Для їх оцінки за вибірковими даними будується логарифмічна функція правдоподібності:

.

Знаходимо похідні

,

.

Запишемо систему рівнянь (33.3):

.

З першого рівняння знаходимо , а з другого

.

Таким чином, згідно з методом максимальної правдоподібності вибірковою оцінкою математичного сподівання є вибіркове середнє. Раніше доведено, що ця оцінка є незміщеною і спроможною. Можна довести, що у випадку нормального розподілу ця оцінка є ефективною. Але вибірковою оцінкою дисперсії є вибіркова дисперсія , яка не є незміщеною.

§34. Розподіл вибіркового середнього і вибіркової дисперсії при нормальному розподілі генеральної ознаки

Вибіркове середнє і вибіркова дисперсія обчислюються за даними вибірки і можуть змінюватись при різних реалізаціях вибірки. Тому величини і є випадковими величинами, знати розподіл яких є практично важливим питанням. Розглянемо розв’язання цього питання за умови, що генеральна ознака розподілена за нормальним законом з математичним сподіванням і дисперсією . Нехай є результат реалізації вибірки. Тоді кожна величина розподілена за нормальним законом з параметрами і .

Згідно з законом великих чисел середнє значення теж розподілене за нормальним законом і, як було показано раніше (див. теорему про не зміщення і (32.6)),

, , .

Тобто математичне сподівання і дисперсія нормального закону для дорівнюють і . Тоді нормована випадкова величина

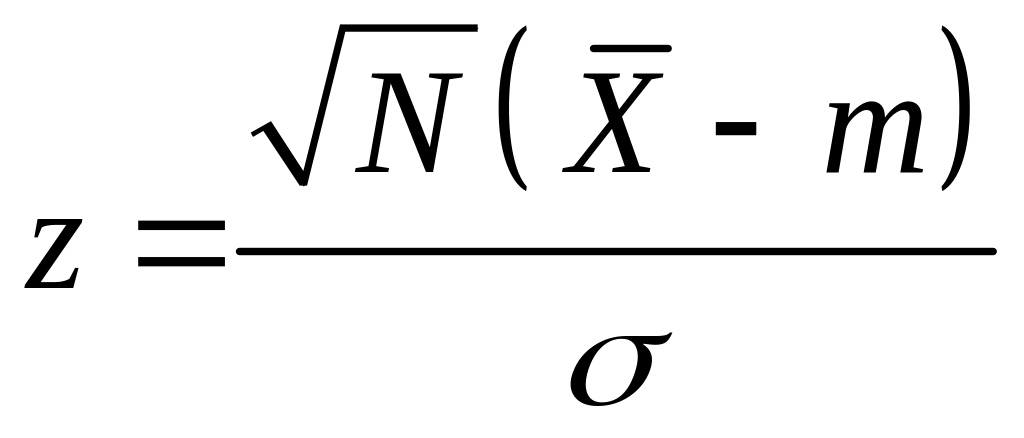
розподілена за нормальним законом з нульовим математичним сподіванням і одиничною дисперсією. Але оскільки дисперсія генеральної ознаки , як правило, невідома, то велике значення має закон розподілу випадкової величини

. (34.1)

Доведено, що закон розподілу цієї величини не залежить від і , а залежить тільки від об’єму вибірки .

Густина розподілу цієї величини називається -розподілом Ст’юдента. Для неї має місце формула

, . (34.2)

Тут функція – гамма-функція [11]. Для практичного застосування складено таблиці функції розподілу Ст’юдента

. (34.3)

Як правило, ці таблиці складені для функції - розподілу Ст’юдента з кількістю ступенів свободи від 1 до 20 (див. додатки). Для більшої кількості ступенів свободи вважається, що випадкова величина розподілена за нормальним законом з , оскільки (34.2) прямує до нього при .

Розглянемо тепер вибіркову дисперсію

.

Останній вираз легко перетворюється до наступного:

.

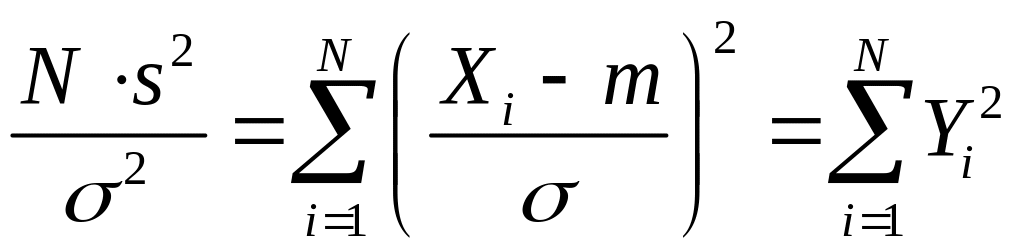Кожна випадкова величина

має і розподілена за нормальним законом. Розглянемо випадкову величину

. (34.4)

Закон розподілу випадкової величини (34.4) не залежить від параметрів розподілу і генеральної ознаки і називається законом розподілу з степенями свободи.

Густина -розподілу з степенями свободи визначається функцією

, . (34.5)

Для практичного застосування складено таблиці ймовірностей

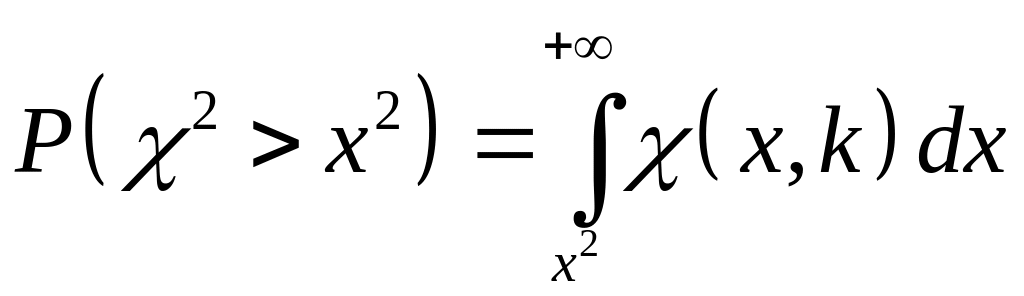(34.6)

для кількості ступеня свободи від 1 до 30 (див. додатки). Якщо кількість ступенів свободи більша за 30, то використовують нормальний закон розподілу, до якого прямує (34.5) при .