Глава V статистичні розподіли і вибіркові оцінки

§31. Основні задачі математичної статистики. Дискретний та інтервальний вибіркові розподіли

В теорії ймовірності при розгляданні випадкових величин не вивчається питання: звідки беруться і як встановлюються закони розподілу випадкових величин. Єдиним шляхом отримання інформації про закони розподілу випадкових величин і їх характеристики (математичне сподівання, дисперсія та інші) є проведення дослідів, випробувань і реєстрація результатів спостережень і вимірювань. В результаті отримуються числові данні, які називаються статистичними. Головними задачами математичної статистики є наступні:

1. Визначення закону розподілу випадкової величини за статистичними даними.

2. Оцінка і визначення невідомих значень параметрів розподілу

3. Перевірка правдоподібності гіпотез щодо законів розподілу.

Основним змістом математичної статистики є систематизація, обробка і використання статистичних даних для виявлення закономірностей ознак деякої сукупності елементів.

Множина усіх однотипних об’єктів, кількісна ознака яких підлягає вивченню, називається генеральною сукупністю. Вважається, що ознака, яка вивчається, є одновимірною або багатовимірною випадковою величиною з невідомим законом розподілу. Оскільки суцільна обробка усіх елементів генеральної сукупності практично неможлива, то, як правило, застосовується вибірковий метод.

Кожна непорожня підмножина випадково вибраних елементів із генеральної сукупності називається вибіркою. Кількість усіх елементів вибірки називають її об’ємом.

Нехай вибірка об’єму . Результатом вибірки є послідовність однаково розподілених випадкових величин, що мають такий самий закон розподілу, як і . Вважається, що коли здійснюється вибірка, кількісна ознака набуває конкретного значення , яке називають варіантою. Кожна варіанта вибірки може бути спостережена разів. Число називають частотою варіанти вибірки .

Нехай – кількість варіант, які різняться числовими значеннями, а – самі ці варіанти розміщені у порядку зростання. Очевидно, що сума частот всіх цих варіант має дорівнювати загальному об’єму вибірки

. (31.1)

Відношення частоти варіанти до загального об’єму вибірки називається відносною частотою варіанти і позначається :

. (31.2)

Очевидно, що відносна частота варіанти є статистичною ймовірністю події :

.

З (31.1) і (31.2) випливає, що для будь-якої вибірки об’єму , виконується рівність:

.

Зростаючу числову послідовність варіант називають варіаційним рядом.

Перелік варіант варіаційного ряду і відповідних їм частот або відносних частот називають дискретним статистичним розподілом випадкової величини .

Дискретний статистичний розподіл може бути записаний у вигляді таблиці:

Дискретний статистичний розподіл дає можливість знайти емпіричну або статистичну функцію розподілу.

Емпіричною (вибірковою) функцією розподілу називається відносна частота події

, (31.3)

де – кількість варіант . Тому можна записати

. (31.4)

Легко перевірити наступні властивості емпіричної функції розподілу:

1. ;

2. ;

3. ;

4. – неспадна функція: .

Дискретний статистичний розподіл можна зобразити графічно у вигляді ламаної лінії (рис. 14), відрізки якої з’єднують точки з координатами або

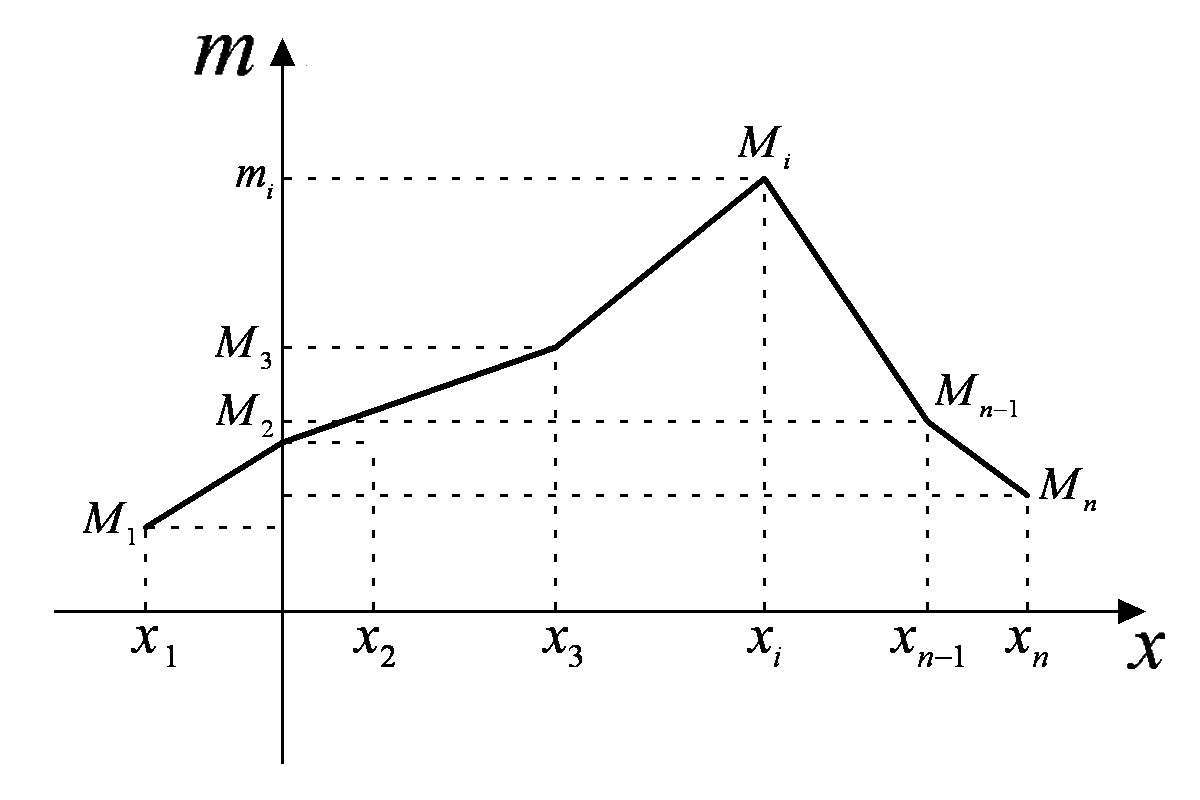
Рис. 14

У випадку, коли – неперервна величина або об’єм вибірки досить великий, результат подають у вигляді інтервального ряду. Для цього область зміни за даними вибірки розбивається на інтервалів . Потім позначаються частоти влучення у кожний інтервал або відносні частоти (статистичні ймовірності) влучення у кожний інтервал:

. (31.5)

Інтервальний ряд оформлюється у вигляді таблиці:

Очевидно, що

. (31.6)

Інтервальний статистичний розподіл зображують графічно у вигляді гістограми частот або гістограми відносних частот.

Гістограма (рис. 15) відносних частот є фігурою, яка складається з прямокутників з основою і висотою .

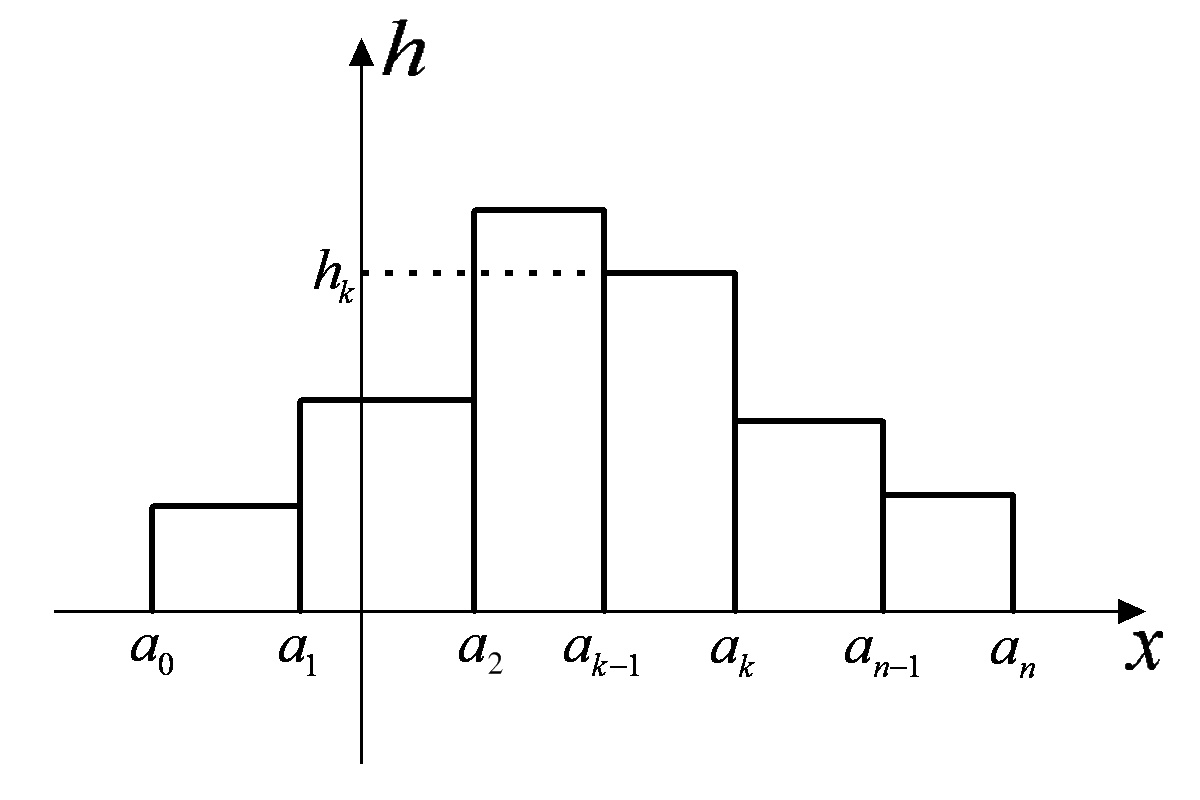
Рис. 15

При побудові гістограми частот висота -го прямокутника дорівнює . Очевидно, що площа -го прямокутника дорівнює , а тому згідно (31.6) виконується рівність:

.

Гістограма відносних частот є наближеним зображенням графіка вибіркової густини розподілу , для якої вважаємо, що при .