Точная формулировка

Теорема Лопиталя:

1. либо ;

2. и дифференцируемы в проколотой окрестности ;

3. в проколотой окрестности ;

4. существует ,

тогда существует .

Пределы также могут быть односторонними.

функция — это правило, по которому каждому элементу одного множества (называемого областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Область определения функции — множество, на котором задаётся функция. В функции "y = f (x)" Это все значения, которые может принимать x.

Подставить отрицательное значание, если функция поменяет знак, то она нечетна, не поменяет-четна. f(-x)=- f(x) нечетная f(-x)=f(x) четная, начальная функция f(x)

Интервалы монотонности функции. Функцию мы называем возрастающей (убывающей) в некотором промежутке , если для любых и из таких, что , выполняется неравенство .

Теорема (достаточное условие монотонности функции). Если производная функции положительна (отрицательна) в некотором интервале , то функция возрастает (убывает) в этом интервале.

Доказательство.

Возьмем два значения аргумента из интервала и , причем , и применим к отрезку теорему Лагранжа:

,

где - некоторая точка из интервала .

Так как по выбору точек, то знак разности совпадает со знаком , т.е. со знаком производной в интервале , откуда и следует утверждение теоремы.

Пример. Найдите интервалы монотонности функции .

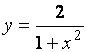Решение.

. Находим производную функции

.

При , т.е. функция возрастает в интервале , а если , то , т.е. функция убывает в интервале .

Ответ: функция возрастает в и убывает в .

15.4. Асимптоты

    Определение 6. Если функция f задана для всех x > a (соответственно для всех x < a) и существует такая прямая

y = kx + l,

(15.20)

что

[f(x) - (kx + l)] = 0

(15.20)

(соответственно при x - ), то эта прямая называется асимптотой функции f при x + (соответственно при x - ).     Конечно, далеко не всякая функция имеет асимптоты. Существование асимптоты функции означает, что при x + (или при x - ) функция ведет себя "почти как линейная функция", т. е. отличается от линейной функции на бесконечно малую.     Укажем методы отыскания асимптот (15.20). Будем рассматривать лишь случай x + ; для x - вывод уравнения асимптоты производится аналогичным способом. Пусть функция f при x + имеет асимптоту (15.20). Тогда поскольку (1/x) = 0, то из условия (15.21) следует, что тем более

[(f(x) - kx - l)/x] = 0,    т. е.  [(f(x)/x - k - l/x] = 0

откуда

[(f(x)/x] = k.

(15.22)

Если значение k найдено, то значение l находится из условия (15.21):

l = [(f(x) - kx].

(15.23)

    Очевидно, справедливо и обратное утверждение: если существуют такие числа k и l, что выполняется условие (15.23), то прямая y = kx + l является асимптотой функции f при x + , так как из (15.23) сразу следует условие (15.21).

    Пример. Найдем асимптоту функции

(15.24)

Согласно формулам (15.22) и (15.23) имеем ,

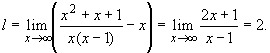
Отсюда следует, что асимптотой функции (15.24) является прямая y = x + 2.     Уравнениями вида (15.20) описываются все прямые, которые не параллельны оси Oy, т. е. не вертикальны. Поэтому асимптоты вида (15.20) называют также и наклонными асимптотами. Сформулируем теперь определение вертикальных асимптот.     Определение 7. Если для функции f выполнено хотя бы одно из условий

f(x) =   или f(x) = б

(15.25)

то прямая x = x₀ называется вертикальной асимптотой функции f.     Для того чтобы имело смысл рассматривать первый (второй) предел (15.25), здесь предполагается, что функция f задана на пересечении некоторой окрестности точки  x₀ с лучом  x < x₀ (с лучом  x > x₀). Чтобы найти вертикальные асимптоты функции f, надо найти такие значения x₀, для которых выполняются одно или оба условия (15.25). Например, для функции (15.24) вертикальной асимптотой является прямая x = 1, ибо

Функции нескольких переменных.

Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

Обычно функция нескольких переменных задается явным аналитическим способом. Например: z=3x+5y²,u=xy+z² и т.д.

В математическом анализе частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.

В явном виде частная производная функции в точке определяется следующим образом:

ледует обратить внимание, что обозначение следует понимать как цельный символ, в отличие от обычной производной функции одной переменной , которую можно представить, как отношение дифференциалов функции и аргумента. Однако, и частную производную можно представить как отношение дифференциалов, но в этом случае необходимо обязательно указывать, по какой переменной осуществляется приращение функции: , где — частный дифференциал функции по переменной . Часто непонимание факта цельности символа является причиной ошибок и недоразумений, как, например, сокращение в выражении . ^[1].