1. Предел функции в точке

Пусть функция у=ƒ (х) определена в некоторой окрестности точки х_о, кроме, быть может, самой точки х_о.

Сформулируем два, эквивалентных между собой, определения предела функции в точке.

Определение 1 (на «языке последовательностей», или по Гейне).

Число А называется пределом функции у=ƒ(х) в топке x₀ (или при х х_о), если для любой последовательности допустимых значений аргумента x_n, n є N (x_nx₀), сходящейся к х_о последовательность соответствующих значений функции ƒ(х_n), n є N, сходится к числу А

В этом случае пишут       или ƒ(х)—>А при х→х_о. Геометрический смысл предела функции: означает, что для всех точек х, достаточно близких к точке х_о, соответствующие значения функции как угодно мало отличаются от числа А.

ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ

Пусть имеем функцию  которая определена в некоторой окрестности  точки . Число называется пределом функции при , если для любого малого наперед заданного положительного числа можно найти такое положительное число  что для всех   удовлетворяющих неравенство

выполняется неравенство

В упрощенной форме определения записывают так

При  функция  является бесконечно большой, если для любого числа можно найти такое число  что для всех , удовлетворяющих неравенство  оправдывается неравенство

В краткой форме это определение примет вид

Функция является бесконечно малой при , если выполняется

ОДНОСТОРОННИЕ ГРАНИЦЫ

Запись можно понимать как приближение к точке слева, когда и дело, когда . аким образом, приближение точек до может быть двусторонним. На основе этого введены определения правой и левой границы.

Число есть пределом функции слева (левой границей), если для любого числа существует такое, что при выполняется неравенство

Число  является пределом функции  справа (правой границей) если для сколь угодно малого значения  найдется  такое что для всех  из промежутка выполняется неравенство

Левая и правая границы называются односторонними границами.

Свойства пределов, связанные с арифметическими операциями над последовательностями

1. Сумма сходящихся последовательностей есть сходящаяся последовательность, предел которой равен сумме пределов исходных последовательностей.

Доказательство .

Пусть , , , - бесконечно малая последовательность, , - бесконечно малая последовательность.

2. Если , , то

3. Если , , то

Доказательство .

, - бесконечно малая последовательность, , - бесконечно малая последовательность.

, где

Лемма . Если ≠ , то начиная с некоторого номера определена последовательность которая является ограниченной.

Доказательство .

Положим

При

при

при

4. Если , ≠ 0, то =

Доказательство .

В силу леммы начиная с некоторого номера N элементы последовательности ограничена. Сэтого номера будем рассматривать последовательность

, - бесконечно малая последовательность.

, - бесконечно малая последовательность.

- бесконечно малая последовательность.

• Первый замечательный предел:

• Второй замечательный предел:

Наряду с непрерывностью функции в точке рассматривают ее непрерывность на разных промежутках.

Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала.

Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b.

Замечание. Функция, непрерывная на отрезке [a,b] может быть разрывной в точках a и b (рис. 1)

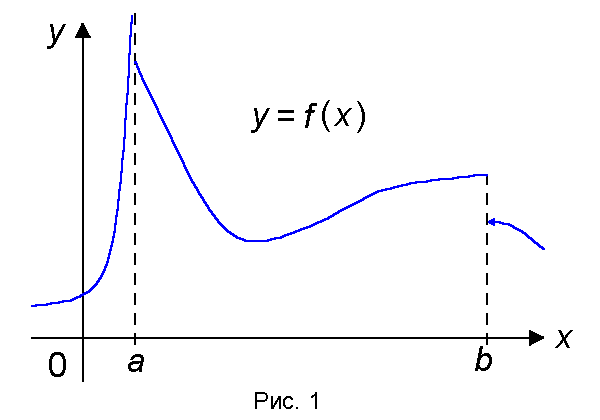
Множество функций, непрерывных на отрезке [a, b] обозначается символом C[a, b].

Свойства функций, непрерывных на отрезке

Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C.

Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β О [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x О [a, b] (рис.2).

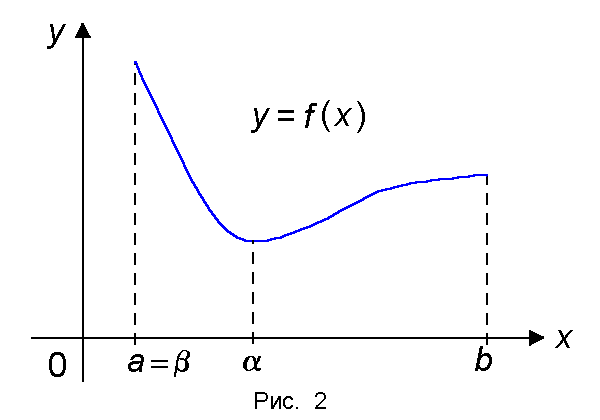
Наибольшее значение M обозначается символом maxx О [a, b] f(x), а наименьшее значение m — символом minx О [a, b] f(x).

Теорема 3 (о существовании нуля). Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0.

Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, обязательно пересечет ось OX (рис.3).

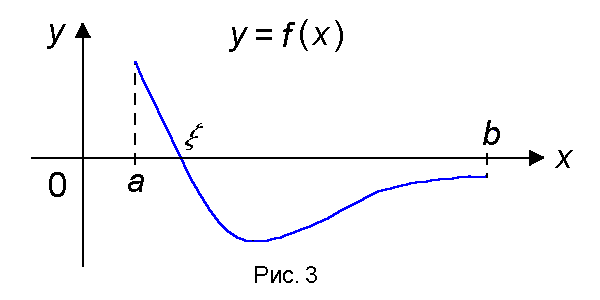
Определение: Производной функции f(x) (f'(x₀)) в точке x₀  называется число, к которому стремится разностное отношение , стремящемся к нулю.

Производные элементарных функций.

Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции  y=f(x) в этой точке