3. Моделирование аэродинамических характеристик несущего винта вертолета

3.1 Основные положения аэроупругой математической модели несущего винта

В настоящей работе для получения необходимых исходных аэродинамических характеристик несущего винта (С_у, m_k, С_х, m_z), использовалась его аэроупругая модель. Данная модель НВ применяется на ОАО КВЗ с 2000 года при расчетном сопровождении летных испытаний и сертификации вертолета «АНСАТ».

Известно, что математическая модель винта вертолета состоит из нескольких важнейших составляющих: аэродинамики, механики и прочности (упругости). Рассмотрим каждую из этих составляющих.

3.1.1. Моделирование упругих деформаций лопасти.

Моделирование упругих деформаций лопасти в пространстве проводится при помощи геометрически нелинейной теории пространственно-деформированных стержней крыльевого профиля.(работы В.А. Павлова и его учеников) В этой теории принято, что упругие перемещения оси стержня после нагрузки могут быть настолько большими, что формы осевой линии в первом и втором состояниях могут значительно различаться друг от друга при условии, что материал лопасти работает в пределах закона Гука.

При изгибе в двух плоскостях применяется гипотеза плоских сечений, а контур сечения не изменяется. Размеры поперечного сечения считаются малыми по сравнению с длиной лопасти и радиусом ее кривизны, то есть лопасть моделируется тонким упругим стержнем. В сечениях лопасти оси жесткости, растяжения и центров масс могут не совпадать.

Согласно теории выражения для кривизны деформированного стержня записываются в виде:

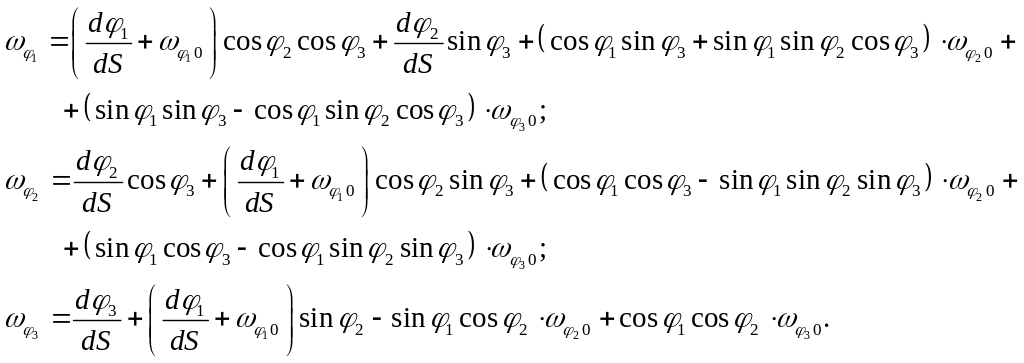(3.1)

где , , – компоненты вектора кривизны; – компоненты вектора кривизны исходного состояния; – угол взмаха каждого элемента лопасти; – угол отставания каждого элемента лопасти; – угол закручивания каждого элемента лопасти.

В качестве физических соотношений, определяющих зависимости между обобщенными деформациями и внешним нагружением, используются известные соотношения Кирхгофа–Клебша. Они основаны на гипотезе Бернулли – Эйлера о том, что для бесконечно малого элемента стержня изгибающие моменты относительно главных центральных осей сечения пропорциональны компонентам вектора кривизны стержня.

(3.2)

где – изгибающие и закручивающий моменты.

Изгибные и крутильные колебания лопасти раскладываются в тригонометрический ряд Фурье. Главная особенность и преимущество данной методики состоит в установлении зависимостей между прогибами, скоростями и ускорениями. Таким образом, задав в первом приближении коэффициенты разложения, принятые в качестве неизвестных параметров, в ряд Фурье, нам известно распределение всех остальных параметров, характеризующих движение лопасти за полный оборот несущего винта, включая скорости и ускорения.

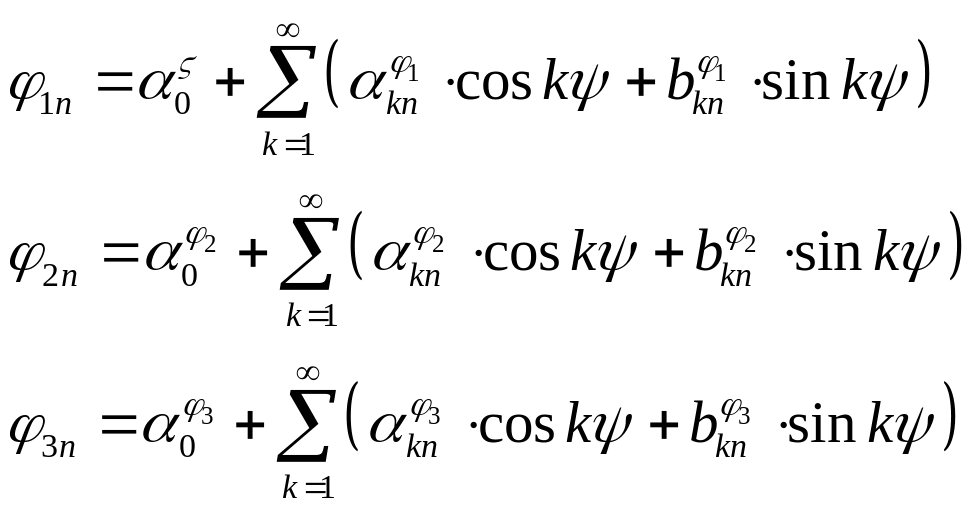(3.3)

где: – коэффициенты разложения;

– азимут лопасти;

 – угловая скорость вращения винта;

t – время;

k – ая гармоника разложения.

Положение упругой линии лопасти с учетом принятой модели определяется при помощи угловых функций ₁(r,); ₂(r,); ₃(r,). При известных величинах коэффициентов разложения можно также вычислить прогибы в любой точке лопасти.

Скорости и ускорения узловых точек в инерциальной системе координат запишутся следующим образом:

(3.4)

(3.5)

Записанные соотношения позволяют определить все параметры пространственного движения лопасти, если известны коэффициенты разложения. Таким образом, основными неизвестными являются коэффициенты разложения, которые необходимо найти для решения системы уравнений.

Далее производим только уточнение коэффициентов разложения в ряд Фурье, используя любой из известных методов численного решения нелинейных уравнений.