14. Движение зарядов в магнитном поле.

Силу действия магн-го поля на движущийся заряд можно найти исходя из закона Ампера. Пусть по проводнику длиной dl за промежуток времени dt проходит n элементарных зарядов величиной q, т.е. через проводник протекает ток, сила которого Согласно закону Ампера, на nq зарядов будет действовать сила Сила, с которой поле действует на каждый заряд, равна Где - скорость движения заряда; α – угол между вектором скорости υ и вектором магн-й индукции B . Сила Лоренца, действующая со стороны магн-го поля на дв-щийся заряд, равна Сила Лоренца, действующая на положительный заряд, перпендикулярна векторам υ и B. Ее направление определяется согласно правилу левой руки:если пальцы направить вдоль вектора скорости заряда, а вектор B входит в ладонь, большой палец показывает направление силы. С изменением знака заряда направление силы изменяется на противоположное. Из (23) можно сделать выводы: – если скорость заряда равна нулю (υ = 0), то 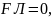т.е. магнитное поле не действует на неподвижную заряженную частицу; – если α = 0, sinα = 0, то FЛ = 0, т.е. если частица движется так, что вектор скорости υ частицы параллелен вектору магнитной индукции B, то магнитное поле на движение заряда не действует. Так как сила Лоренца всегда направлена перпендикулярно вектору скорости частицы, то она не изменяет величину скорости, а изменяет лишь направление движения частицы, т.е. по физической сути является центростремительной силой. Действие этой силы не приводит к изменению энергии заряженной частицы, т.е. эта сила не совершает работы. Если заряд движется в области, где одновременно действуют электрическое и магнитное поля, то результирующая сила, действующая на частицу, равна т.е. сила имеет две составляющие: от воздействия магнитного и электрического полей. Между этими составляющими имеется принципиальная разница. Электрическое поле изменяет величину скорости и кинетическую энергию частицы, а однородное магнитное поле изменяет только направление движения.

16. Эффект Холла.

А мериканский ученый Э. Холл в 1880 году обнаружил, что в проводнике, помещенном в магнитное поле, при опред-х усл-х возникает разность потенциалов между его противоположными пов-тями, параллельными направлению вектора магнитной индукции B и тока I. Опыты показали, что разность потенциалов U определяется равенством , где k – постоянная Холла, зависящая от рода вещества; j – плотность тока в проводнике. Этот эффект объясняется следующим образом. В направлении вектора j свободные электроны проводника движутся со скоростью υ, и на них действует сила Лоренца, равная . В результате все электроны смещаются вверх к плоскости S1, создавая на ней избыточный отрицательный заряд и потенциал (рис. 1.13). На нижней плоскости остается некомпенсированный положительный заряд атомов кристаллической решетки, и потенциал S2 становится положительным. Электрическое поле Е, возникающее в проводнике, действует на электроны с силой . Условие обеспечивает постоянство разности потенциалов U, равной 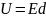. С учетом равновесия сил F_Л и F_E можно записать: . Скорость электронов υ можно выразить через плотность тока j. Так как 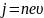, получим . Получаем . 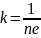Таким образом постоянная Холла зависит от концентрации электронов в проводнике. Следовательно, через постоянную Холла можно определить концентрацию электронов проводимости в проводнике.