1. Параметры электрического поля в некоторой точке пространства от системы точечных зарядов.

Электрическое поле. Силовые взаимодействия между разобщенными телами могут передаваться только при наличии некоторой среды, окружающей эти тела, последовательно от одной части этой среды к другой, и с конечной скоростью. Такой средой является особый вид материи – электрическое поле. Оно является неизменным спутником каждого электрического заряда. Судить о существовании электрического поля в данной точке пространства можно только по наличию силы, с которой поле действует на помещенный в эту точку электрический заряд. Напряженность электрического поля. Вектор, равный отношению силы F, с которой заряд q действует на точечный малый положительный заряд q₀, помещенный в некоторую точку пространства , называют напряженностью эл.поля, создаваемого зарядом q в данной точке. С другой стороны, если напряженность эл поля в данной точке известна, то сила, действующая на помещенный в эту точку заряд q: . Напряженность эл поля точечного заряда q на расстоянии R от него: . Векторы напряженности электрического поля подчиняются принципу суперпозиции. Силовой линией называют такую линию, касательная к которой в каждой точке совпадает с направлением вектора напряженности поля в этой точке. Силовым линиям приписывают определенное направление, отмечая его на чертеже стрелкой в направлении вектора напряженности. При этом силовые линии нигде не пересекаются. В противном случае в точках пересечения вектор напряженности поля имел бы одновременно разные направления. Из определения силовых линий следует, что они начинаются только на положительных зарядах и заканчиваются на отрицательных (или «уходят» на бесконечность от положительного заряда, или «приходят» из бесконечности к отрицательному заряду). Если напряженность электрического поля во всех точках одинакова, то такое поле называют однородным.

Электрический потенциал. Скалярная величина, равная отношению потенциальной энергии заряда q₀ в эл поле заряда q к величине этого заряда: называется потенциалом электрического поля заряда q в данной точке. Подчиняется принципу суперпозиции.

Связь между потенциалом и напряженностью электрического поля. , , производная от функции потенциала = - напряженность: минус показывает, что вектор E направлен туда, где потенциал заряда ниже.

2. Теорема Остроградского-Гаусса для поля распределенных зарядов; ее применение для определения параметров поля бесконечного линейного заряда.

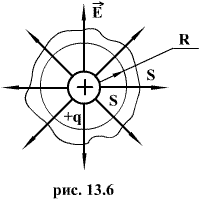
Определим поток напряжённости поля электрических зарядов через некоторую замкнутую поверхность, окружающую эти заряды. Рассмотрим сначала случай сферической поверхности радиуса R, окружающей один заряд, находящийся в ее центре (рис. 13.6). Напряженность поля по всей сфере одинакова и равна .

Силовые линии направлены по радиусам, т.е. перпендикулярны поверхности сферы S_n , следовательно т.к. Тогда поток напряженности будет равен . Используя формулу напряжённости, находим

Окружим теперь сферу произвольной замкнутой поверхностью S’. Каждая силовая линия, пронизывающая сферу, пронижет и эту поверхность. Следовательно формула справедлива не только для сферы, но и для любой замкнутой поверхности. Если произвольной поверхностью окружаем n зарядов, то очевидно, что поток напряженности через эту поверхность равен сумме потоков, создаваемых каждым из зарядов, т.е. , или

Т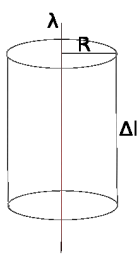 аким образом, полный поток вектора напряженности электростатического поля через замкнутую поверхность произвольной формы численно равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности, поделенной на . Это положение называется теоремой Остроградского - Гаусса. С помощью этой теоремы можно определить напряженность полей, создаваемых заряженными телами различной формы.

Расчёт напряжённости поля бесконечной нити.

Рассмотрим поле, создаваемое бесконечной прямолинейной нитью с линейной плотностью заряда, равной λ. Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии R от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом R и высотой Δl. Тогда поток напряжённости через эту поверхность по теореме Гаусса таков (в единицах СИ): В силу симметрии вектор напряженности поля направлен перпендикулярно нити, прямо от нее (или прямо к ней); модуль этого вектора в любой точке поверхности цилиндра одинаков. Тогда поток напряжённости через эту поверхность можно рассчитать следующим образом: Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю (вследствие направления E по касательной к ним). Приравнивая два полученных выражения для , имеем: