
- •Содержание
- •Раздел 1. Федеральный закон от 9 февраля 2007 г. № 16-фз «о транспортной безопасности» 4
- •Раздел 2. Статистическая теория безопасности движения поездов 21
- •Раздел 3. Применение методологии урран при оценке рисков для систем железнодорожной автоматики и телемеханики 72
- •Раздел 4. Практикум 82
- •Введение
- •Раздел 1. Федеральный закон от 9 февраля 2007 г. № 16-фз «о транспортной безопасности»
- •Раздел 2. Статистическая теория безопасности движения поездов
- •2.1 Перевозочные процессы
- •2.1.1 Характеристики перевозочных процессов
- •2.1.2 Состояния перевозочных процессов
- •2.1.3 Дестабилизирующие факторы перевозочных процессов
- •2.1.4 Безопасность перевозочного процесса и риски потерь
- •2.2 Процесс движения поезда
- •2.2.1Состояния процесса движения поезда
- •2.2.2 Дестабилизирующие факторы процесса движения
- •2.2.3 Поражающие факторы
- •2.2.4 Безопасность движения поезда и риски потерь
- •2.3 Анализ безопасности движения поездов
- •2.3.1 Цель и методы анализа
- •2.3.2 Процедура анализа
- •2.3.3 Концепция частотного анализа Sok, Hj, Мi и Ni
- •2.3.4 Концепция определения потерь и экономического ущерба
- •23.5 Расследование причин возникновения опасных состояний
- •2.4 Основы обеспечения безопасности движения поездов
- •2.4.1 Методы повышения безопасности
- •2.4.2 Обеспечение безопасности деятельности персонала
- •2.4.3 Методы снижения потерь
- •Раздел 3. Применение методологии урран при оценке рисков для систем железнодорожной автоматики и телемеханики
- •Раздел 4. Практикум
- •4.1 Исходные данные для задания 1
- •4.2 Методические указания для выполнения задания 1
- •4.3 Пример выполнения задания 1
- •4.4 Исходные данные для задания 2
- •4.5 Методические указания для выполнения задания 2
- •4.6 Пример выполнения задания 2
- •Литература
4.5 Методические указания для выполнения задания 2
Определение риска по безотказности для ОИ.
Согласно методам
теории массового обслуживания, параметр
 можно рассматривать как среднее время
простоя одного поезда:
можно рассматривать как среднее время
простоя одного поезда:
|
(1) |
где  ;
;
 ;
;
 ;
;
 – удельная
нагрузка по использованию элемента ОИ;
– удельная
нагрузка по использованию элемента ОИ;
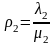 – удельная
нагрузка по устранению отказов элемента
ОИ;
– удельная
нагрузка по устранению отказов элемента
ОИ;
 – среднее время
пропуска поезда по элементу ОИ, ч;
– среднее время
пропуска поезда по элементу ОИ, ч;
 ;
;
 – количество
поездов, пропускаемых по элементу ОИ
за расчётный период
;
– количество
поездов, пропускаемых по элементу ОИ
за расчётный период
;
 – второй начальный
момент длительности пропуска поездов
по элементу ОИ;
– второй начальный
момент длительности пропуска поездов
по элементу ОИ;
 ;
;
 – второй начальный
момент длительности устранения отказа
элемента ОИ;
– второй начальный
момент длительности устранения отказа
элемента ОИ;
 ;
;
 – количество
отказов элемента ОИ за расчётный период
.
– количество
отказов элемента ОИ за расчётный период
.
Среднее число простаивающих поездов определяется как:
|
(2) |
Окончательно,
среднее число
 и время дополнительных остановок поездов
и время дополнительных остановок поездов
 ,
[ч] вследствие отказов элемента ОИ
определяются по формулам:
,
[ч] вследствие отказов элемента ОИ
определяются по формулам:
 ,
,
 ,
(3)
,
(3)
где
 ,
,
 - средняя длина очереди поездов и число
простаивающих поездов при отсутствии
отказов элемента ОИ;
- средняя длина очереди поездов и число
простаивающих поездов при отсутствии
отказов элемента ОИ;
 ,
,
 - средняя длина очереди поездов и число
простаивающих поездов при наличии
отказов элемента ОИ интенсивностью
.
- средняя длина очереди поездов и число
простаивающих поездов при наличии
отказов элемента ОИ интенсивностью
.
Суммарный ущерб
от отказов ОИ вследствие простоя поездов
за расчётный период
 [тыс. руб.] вычисляют по формуле:
[тыс. руб.] вычисляют по формуле:
 , (4)
, (4)
где – средняя стоимость одного часа простоя поезда, тыс. руб.
- количество элементов ОИ.
Суммарный ущерб
от отказов ОИ вследствие дополнительных
остановок поездов за расчётный период
 [тыс. руб.] вычисляют по формуле:
[тыс. руб.] вычисляют по формуле:
 , (5)
, (5)
где – средняя стоимость дополнительной остановки поезда, тыс. руб.
Суммарный ущерб по ОИ составляет:
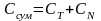 , (6)
, (6)
Значения вероятностей состояний НЗЭО определяется по следующим формулам:
– вероятность использования элемента ОИ:
|
(7) |
где  ;
;
 ;
;
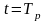 ;
;
– вероятность отказа элемента ОИ:
|
(8) |
Вероятность риска по безотказности для ОИ:
|
(9) |
Таким образом, определены показатель для оценки вероятности риска по безотказности для ОИ и показатель, характеризующий последствия риска по безотказности для ОИ. Полученные показатели используются при анализе риска по безотказности для ОИ на различных этапах жизненного цикла с помощью матриц риска. В табл. 9 приведена матрица рисков по безотказности для ОИ. Согласно данной матрице определяется уровень риска для ОИ.
Таблица 9 – Матрица риска по безотказности для ОИ
Вероятность риска |
Уровни тяжести последствий (величина ущерба) |
||||||||||
< 50 тыс. руб. |
50 – 200 тыс. руб. |
200 – 4000 тыс. руб. |
4000 – 20000 тыс. руб. |
> 20000 тыс. руб. |
|||||||
незначительный |
серьёзный |
критический |
катастрофический |
бедственный |
|||||||
0,9 ≤ PОИ ≤ 1 |
Частое |
Ч1 |
Ч2 |
Ч3 |
Ч4 |
Ч5 |
|||||
0,1 ≤ PОИ < 0,9 |
Вероят-ное |
В1 |
В2 |
В3 |
В4 |
В5 |
|||||
10-3 ≤ PОИ < 0,1 |
Случай-ное |
С1 |
С2 |
С3 |
С4 |
С5 |
|||||
10-5 ≤ PОИ < 10-3 |
Редкое |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
|||||
10-7 ≤ PОИ < 10-5 |
Крайне редкое |
К1 |
К2 |
К3 |
К4 |
К5 |
|||||
PОИ < 10-7 |
Мало-вероятное |
М1 |
М2 |
М3 |
М4 |
М5 |
|||||
Определение риска по безопасности для ОИ.
Определение риска по безопасности для ОИ основывается на теории случайных импульсных потоков. Интенсивность отказов ОИ, которые могу привести к нарушению безопасности движения поездов, определяется по формуле:
|
(10) |
Средняя длительность активного состояния ОИ:
|
(11) |
Средняя длительность пассивного состояния ОИ:
|
(12) |
Средняя длительность соответственно опасного и неопасного состояний ОИ:
|
(13) |
|
(14) |
Математическое ожидание длительности совпадения активных и опасных состояний ОИ равно:
|
(15) |
Среднюю интенсивность перехода ОИ в активное опасное состояние можно определить по формуле:
|
(16) |
Среднюю длительность совокупности следующих состояний ОИ: пассивного опасного, активного неопасного и пассивного неопасного можно определить по формуле:
|
(17) |
При допущении о
том, что случайная величина
 распределена по экспоненциальному
закону, параметр закона распределения
можно определить
как:
распределена по экспоненциальному
закону, параметр закона распределения
можно определить
как:
|
(18) |
За расчётное время вероятность возникновения риска для ОИ по безопасности при движении поездов определяется по формуле:
|
(19) |
В табл. 10 приведена матрица рисков по безопасности для ОИ. Согласно данной матрице определяется уровень риска для ОИ.
Таблица 10 – Матрица риска по безопасности для ОИ
Вероятность риска |
Уровни тяжести последствий (величина ущерба) |
||||||||||
незначительный |
серьёзный |
критический |
катастрофический |
бедственный |
|||||||
0,9 ≤ PОИ ≤ 1 |
Частое |
Ч1 |
Ч2 |
Ч3 |
Ч4 |
Ч5 |
|||||
0,1 ≤ PОИ < 0,9 |
Вероят-ное |
В1 |
В2 |
В3 |
В4 |
В5 |
|||||
10-3 ≤ PОИ < 0,1 |
Случай-ное |
С1 |
С2 |
С3 |
С4 |
С5 |
|||||
10-5 ≤ PОИ < 10-3 |
Редкое |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
|||||
10-7 ≤ PОИ < 10-5 |
Крайне редкое |
К1 |
К2 |
К3 |
К4 |
К5 |
|||||
PОИ < 10-7 |
Мало-вероятное |
М1 |
М2 |
М3 |
М4 |
М5 |
|||||

 ,
, .
. ,
, .
. .
. ,
, ,
, ,
, ,
, .
. ,
, ,
, ,
,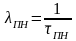 ,
, ,
,