МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ

СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ

Кафедра ФИЗИКИ И ФИЗИЧЕСКОГО МАТЕРИАЛОВЕДЕНИЯ

ПРИКЛАДНАЯ ФИЗИКА

(КОНСПЕКТ ЛЕКЦИЙ)

Ч. 1. Механика, Основы молекулярной физики и термодинамики, Электричество и Магнетизм

(для студентов дневной и заочной формы обучения)

всех специальностей профессиональных направлений

«Инженерная механика»

код дисциплины - 0801

УТВЕРЖДЕНО

на заседании кафедры ФФМ

протокол № 1 от 30.08.2014г.

Зав. кафедрой ФФМ

д.х.н., проф. Александров В.Д.

г. Макеевка, ДонНАСА

2014

УДК: 531.6(071)

Физика. Курс лекций по прикладной физике (часть 1).

Сост.: к.х.н., доц. О.В. Соболь. Под редакцией доктора химических наук, профессора Александрова В.Д. – г. Макеевка: ДонНАСА, 2014. – 95 с.

Рецензент: Тимченко В.И., к.ф.-м.н., доц., зав. каф. «Электротехника и

автоматика» Донбасской национальной академии

строительства и архитектуры.

Ответственный за выпуск: к.х.н., доц. Соболь О.В.

Оглавление

Механика

ЛЕКЦИЯ 1 и 2. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ

1. Система отсчета. Траектория, длина пути, вектор перемещения

2. Скорость

3. Ускорение и его составляющие

4. Угловая скорость и угловое ускорение

ЛЕКЦИЯ 3 и 4. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

1. Первый закон Ньютона. Масса. Сила

2. Основной закон динамики поступательного движения

3. Третий закон Ньютона

ЛЕКЦИЯ 5. ЭНЕРГИЯ, КАК УНИВЕРСАЛЬНАЯ МЕРА РАЗЛИЧНЫХ ФОРМ ДВИЖЕНИЯ И ВЗАИМОДЕЙСТВИЯ ТЕЛ. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ

1. Энергия, механическая работа, мощность

2. Кинетическая и потенциальная энергии

3. Законы сохранения импульса и энергии

ЛЕКЦИЯ 6 и 7. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

1. Момент силы

2. Пара сил

3. Простые механизмы

4. Момент инерции

5. Кинетическая энергия вращения

6. Уравнение динамики вращательного движения твердого тела

7. Момент импульса и закон его сохранения

ЛЕКЦИЯ 8. ЭЛЕМЕНТЫ МЕХАНИКИ ЖИДКОСТЕЙ И ГАЗОВ

1. Гидростатика. Закон Архимеда. Атмосферное давление

2. Давление в жидкости и газе. Закон Паскаля

3. Уравнение неразрывности

4. Уравнение Бернулли и следствия из него

5. Ламинарный и турбулентный режимы течения жидкостей

6. Движение тел в жидкостях и газах

Основы молекулярной физики и термодинамики

ЛЕКЦИЯ 9 и 10. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ

1. Введение. Законы идеального газа. Уравнение Менделеева-Клайперона

2. Основное уравнение молекулярно-кинетической теории идеальных газов

3. Закон Максвелла о распределении молекул идеального газа по скоростям

4. Барометрическая формула. Распределение Больцмана

5. Среднее·число столкновений и средняя длина свободного пробега молекул

ЛЕКЦИЯ 11. ОСНОВЫ ТЕРМОДИНАМИКИ

1. Введение в термодинамику

2. Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы молекул

3. Первое начало термодинамики

4. Работа газа при изменении его объема

5. Теплоемкость

6. Применение первого начала термодинамики к изопроцессам

ЛЕКЦИЯ 12. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ

1. Круговой процесс (цикл). Обратимые и необратимые процессы

2. Приведенное количество теплоты. Энтропия

3.Второе начало термодинамики

4. Тепловые двигатели и холодильные машины. Цикл Карно и его к.п.д. для идеального газа

ЛЕКЦИЯ 13. РЕАЛЬНЫЕ ГАЗЫ И ЖИДКОСТИ

1. Уравнение Ван-дер-Ваальса

2. Изотермы Ван-дер-Ваальса и их анализ

3. Внутренняя энергия реального газа

4. Поверхностное натяжение

5. Явление смачивания

6. Давление под искривленной поверхностью жидкости

7. Капиллярные явления

Электричество и магнетизм

ЛЕКЦИЯ 14. ОСНОВЫ ЭЛЕКТРОСТАТИКИ

1. Закон сохранения заряда и закон Кулона

2. Поток вектора напряженности

3. Теорема Гаусса

4. Поле бесконечной однородно заряженной плоскости

5. Поле двух разноименно заряженных плоскостей

6. Поле бесконечно заряженного цилиндра

7. Работа сил электростатического поля

8. Потенциал

9. Связь между напряженностью электрического поля и потенциалом

10. Эквипотенциальные поверхности

11. Полярные и неполярные молекулы

12. Диполь в однородном и неоднородном электрических полях

13. Поляризация диэлектриков

14. Поле внутри плоской пластины

15. Электроемкость

16. Конденсаторы

17. Энергия системы зарядов

ЛЕКЦИЯ 15 и 16. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК. РАБОТА И МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА.

1. Электрический ток, сила и плотность тока

2. Сторонние силы. Электродвижущая сила и напряжение

3. Закон Ома. Сопротивление проводников

4. Работа и мощность тока. Закон Джоуля – Ленца

5. Закон Ома для неоднородного участка цепи

6. Правила Кирхгофа для разветвленных цепей

ЛЕКЦИЯ 17. МАГНИТНОЕ ПОЛЕ

1. Магнитное поле и его характеристики

2. Закон Био – Савара – Лапласа и его применение к расчету магнитного поля

3. Закон Ампера. Взаимодействие параллельных токов

4. Действие магнитного поля на движущийся заряд

5. Циркуляция вектора В магнитного поля в вакууме

6. Магнитные поля соленоида и тороида

7. Поток вектора магнитной индукции. Теорема Гаусса для поля В

8. Работа по перемещению проводника и контура с током в магнитном поле

9. Явление электромагнитной индукции (опыты Фарадея)

10. Вращение рамки в магнитном поле

11. Индуктивность контура. Самоиндукция

12. Взаимная индукция

13. Трансформаторы

14. Энергия магнитного поля

Механика кинематика материальной точки

1. Система отсчета. Траектория, длина пути, вектор перемещения

Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.

Механическое движение – это изменение с течением времени взаимного расположения тел или их частей.

Механика для описания движения тел в зависимости от условий конкретных задач использует разные физические модели. Простейшей моделью является материальная точка – тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Например, изучая движение планет по орбитам вокруг Солнца, можно принять их за материальные точки.

Под воздействием тел друг на друга они могут деформироваться, т.е. изменять свою форму и размеры. Поэтому в механике вводится еще одна модель – абсолютно твердое тело. Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться.

Л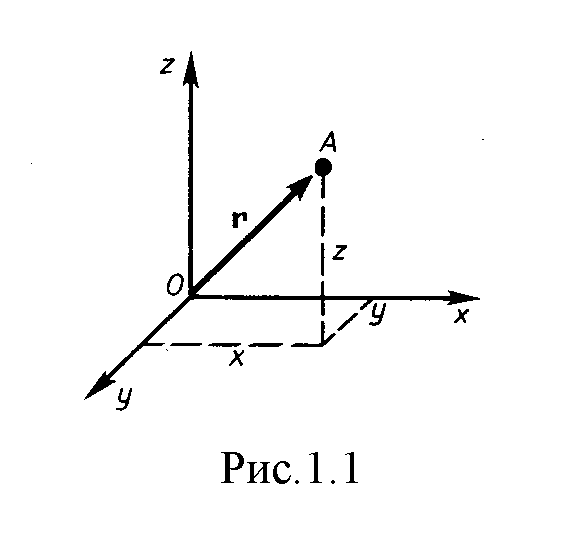 юбое движение твердого тела можно представить как комбинацию поступательного и вращательного движений. Поступательное движение – это движение, при котором все точки тела описывают одинаковые траектории или любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения, за исключением одной, которая называется центром.

Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени t она проходила то или иное положение. В системе СИ время измеряется в секундах [t] = c.

Положение материальной точки определяется по отношению к какому-либо другому, произвольно выбранному телу, называемому телом отсчета. С ним связывается система отсчета – совокупность системы координат и часов, связанных с телом отсчета. В декартовой системе координат положение точки А в данный момент времени характеризуется тремя координатами х, у и z или радиусом-вектором , проведенным из начала системы координат в данную точку (рис. 1.1).

При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется кинематическими уравнениями в скалярной форме

x = x(t), y = y(t), z = z(t), (1.1)

или в векторной форме

(t). (1.2)

Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы i. Если материальная точка свободно движется в пространстве, то i=3.

Исключая t в уравнениях (1.1) и (1.2), получим уравнение траектории движения материальной точки. Траектория движения материальной точки –линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.

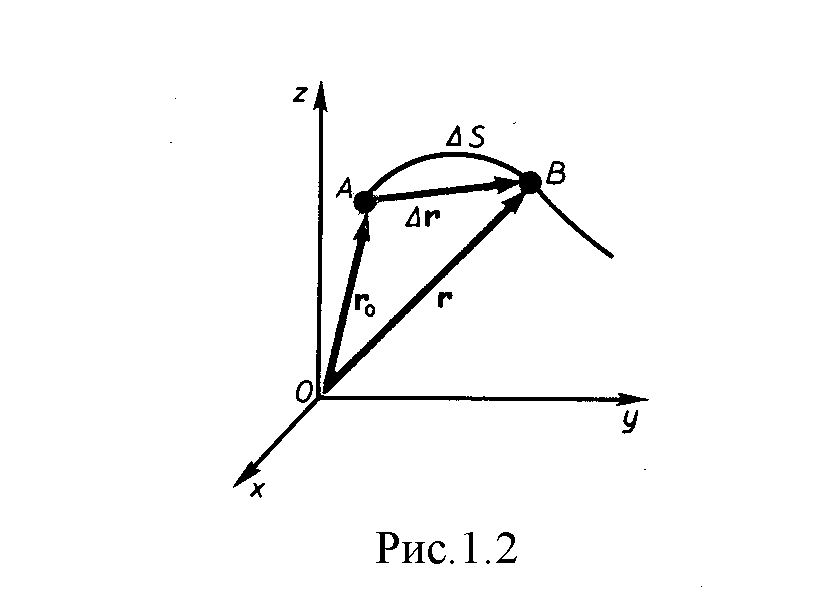
Рассмотрим движение материальной точки вдоль произвольной траектории (рис. 1.2). Отсчет времени начнем с момента, когда точка находилась в положении А. Длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени, называется длиной пути Δs и является скалярной функцией времени: Δs = Δs(t). Размерность пути в СИ – метр (м). Вектор , проведенный из начального положения движущейся точки в конечное ее положение называется перемещением. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль пе­ремещения равен пройденному пути Δs.