Лекція 12 швидкість та прискорення точки

12.1. Швидкість точки при векторному способі задання її руху

Швидкість – це фізична величина, що показує в якому напрямі та на яку відстань перемістилась точка у просторі за одиницю часу.

Прискорення точки – це фізична величина, яка характеризує зміну швидкості точки за часом.

Зупинимося на визначенні швидкості при трьох способах задання руху точки.

Р ух точки задано рівнянням . Нехай у момент часу положення рухомої точки М визначається радіусом-вектором , а в момент часу радіусом-вектором (рис. 11.1). Приріст радіуса-вектора за час є вектор переміщення точки за цей проміжок часу.

Відношення вектора переміщення точки до відповідного проміжку часу , називається вектором середньої швидкості руху точки по хорді _.

. (12.1)

При зменшенні і наближенні його до нуля середня швидкість наближується до швидкості точки у даний момент часу:

,

Тобто

. (12.2)

Отже, вектор швидкості точки в даний момент часу дорівнює першій похідній за часом від радіуса-вектора точки.

Спрямований вектор швидкості по дотичній до траєкторії у бік руху точки. Це витікає з того, що граничним положенням січної , по якій спрямований вектор середньої швидкості точки, є дотична до траєкторії у точці .

12.2. Швидкість точки при координатному способі задання іі руху

Нехай рух точки задано у декартовій системі координат рівняннями: ; ; (рис. 12.2). Згадаємо, що радіус-вектор точки можна виразити через його проекції x, y, z таким чином:

, (12.3)

де , і – сталі величини.

На підставі (12.2), і враховуючи (12.3), маємо:

. (12.4)

З іншого боку, вектор швидкості точки можна також розкласти на складові за координатними осями

. (12.5)

Порівнюючи формули (12.4) і (12.5), одержимо:

; ; . (12.6)

Отже, проекції вектора швидкості точки на осі декартових координат дорівнюють першим похідним за часом від відповідних координат точки.

Модуль і напрямні косинуси вектора швидкості точки визначають за формулами:

; (12.7)

; ; .

Одиницями вимірювання швидкості є см/сек , м/сек, або км/год.

12.3. Швидкість точки при натуральному способі задання її руху

Нехай рух точки задано натуральним способом, тобто відомі траєкторія, початок і додатний напрям дугової координати , а також рівняння руху точки за цією траєкторією (рис. 12.2).

Із довільної точки О проведемо радіус-вектор точки М.

Будемо розглядати цей вектор як складну функцію часу

. (12.8)

На підставі (12.2), враховуючи (12.8), одержимо вектор швидкості точки у такому вигляді:

. (12.9)

Розглянемо перший співмножник виразу (12.9) у такій формі:

.

Як витікає з рис. 12.2, модуль цього вектора, як границя відношення довжини нескінченно малої хорди до довжини стягнутої нею дуги , дорівнює:

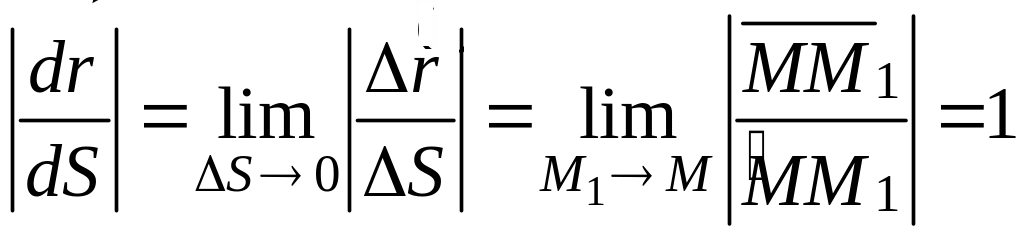. (12.10)

Напрям одиничного за величиною вектора (12.10) завжди збігається з напрямом дотичної в бік збільшення дугової координати, тобто

, (12.11)

де – орт дотичної до траєкторії.

З урахуванням (12.11) вираз (12.9) набуває вигляду:

, (12.12)

де

. (12.13)

Із (12.13) видно, що може бути більше або менше від нуля в залежності від того, збільшується або зменшується дугова координата рухомої точки.

Тому , що дорівнює першій похідній за часом від дугової координати, являє собою проекцію вектора швидкості на дотичну, тобто визначає алгебраїчну величину швидкості.

Отже, вектор швидкості при натуральному способі задання руху точки дорівнює добутку проекції швидкості на дотичну до траєкторії і орта дотичної .