11.6. Перехід від координатного до натурального способу задання руху точки
Нехай рух точки дано в декартових координатах рівняннями (11.2). Щоб перейти до натурального способу, треба знайти рівняння траєкторії точки у координатній формі, вилучивши з (11.2) час , визначити цю траєкторію , а потім знайти рівняння руху точки за траєкторією: .
Як відомо, модуль диференціала дугової координати дорівнює:
,
де
можна вважати, що:
.
Враховуючи,
що при
=0
дугова координата
,
для
визначення рівняння
руху
точки за траєкторією одержимо таку
формулу :
.
(11.6)
11.7. Приклади розв’язання задач
Приклад 1. Рух точки задано рівняннями:
;
.
Визначити рівняння траєкторії точки.
Р
озв’язання.
3 першого рівняння знайдемо час
t
і, підставляючи його значення у друге,
одержимо рівняння траєкторії точки в
координатній формі:
.
Це
рівняння прямої, але траєкторією буде
не вся пряма, а тільки та її частина, по
якій рухається точка. З рівнянь руху
витікає, що на початку руху (
)
точка
мала координати
=0,
=b.
Із збільшенням часу координати точки
збільшуються.
Отже, траєкторією точки буде та частина прямої, яка на рис. 11.4 показана суцільною лінією.
Приклад 2. Рух точки задано у декартових координатах рівняннями:
;
,
де
,
і
– сталі. Перейти до натурального способу
задання руху точки.
Розв’язання.
Із заданих рівнянь вилучимо час
.
Для цього у першому рівнянні величину
переносимо в ліву частину. Далі, підносимо
обидва рівняння у другий ступінь і
додавши їх, отримаємо рівняння траєкторії
точки у координатній формі:
.
Т
раєкторія
точки – коло радіуса
,
центр якого має координати
(рис. 11.5).
При
координати точки
,
,
тобто точка знаходилась в положенні
.
З рівнянь руху виходить, що за зростанням
координата
зменшується, а координата
збільшується. Отже, точка з початкового
положення
рухається у напрямку, що показано
стрілкою на рис. 11.5.
Обчислюємо похідні від заданих рівнянь:
;
.
За формулою (11.6) одержимо рівняння руху точки за траєкторією:
=
.
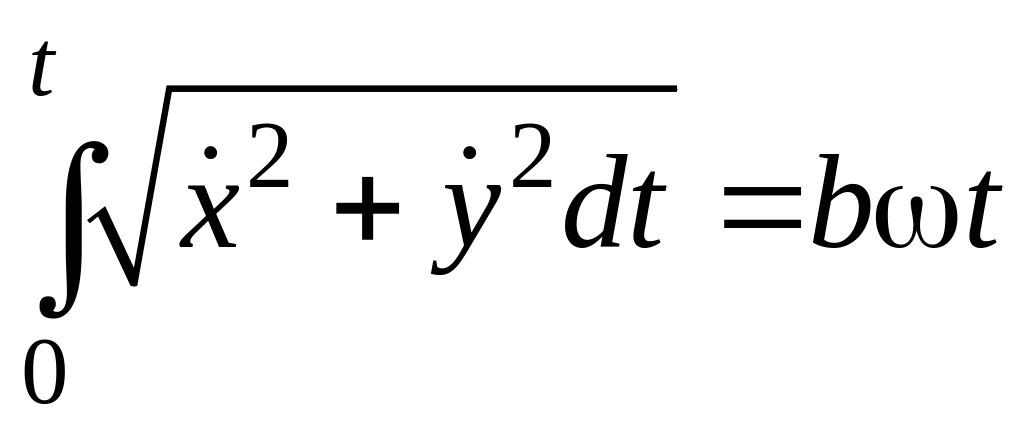Отже, точка описує коло радіуса b з центром С так, що її дугова координата збільшується пропорційно часу за лінійним законом.
Приклад 3. За заданими рівняннями руху точки
;
знайти рівняння її траєкторії, визначити цю траєкторію, а також знайти закон руху точки за траєкторією, відраховуючи відстань від початкового положення точки.
Р
озв’язання.
Рівняння траєкторії точки у координатній
формі – рівняння прямої
.
Траєкторія
точки – це відрізок прямої, позначений
на рис. 11.6
суцільною лінією. Рух точки починається
з положення
.
Через час
точка займе положення
,
а через
повернеться у точку
.
Враховуючи формулу (11.6) знаходимо рівняння руху за траєкторією:
,
;
Отже,
точка рухається вздовж відрізка
в його межах за гармонійним законом,
тобто відстань
М
відповідно збільшується або зменшується.
Приклад 4. Рух точки, що описує фігуру Ліссажу, задається рівняннями:
;
.
Знайти рівняння траєкторії точки, побудувати цю траєкторію та визначити напрям руху точки у різні моменти часу. Знайти також найближчий після початку руху момент часу , коли траєкторія перетинає вісь Ох.
Розв’язання.
Враховуючи
обмеження з рівнянь руху точки
;
,
встановлюємо область розташування
траєкторії точки (рис. 11.7).
З
найдемо
рівняння траєкторії у координатній
формі, вилучивши з рівнянь руху параметр
.
Для цього з першого рівняння виділимо:
і піднесемо до квадрату:
.
Використовуючи формулу з тригонометрії
,
запишемо:
.
Звідки отримуємо:
.
Це
рівняння квадратної параболи з
вертикальною віссю симетрії
.
Траєкторією
точки
є верхівка цієї параболи, що знаходиться
у середині визначеної області
і
показана на рис. 11.7 суцільною лінією.
Момент
часу
– момент перетину точкою
осі
після початку руху відповідає координаті
.
Враховуючи,
що
,
маємо:
;
,
тобто
.