МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОАЛЬНИЙ УНІВЕРСИТЕТ «КИЄВО-МОГИЛЯНСЬКА АКАДЕМІЯ»
Факультет економічних наук
Кафедра фінансів
Домашня робота №3
з курсу «Економетрика»
Виконала: студентка ФЕН-3, спеціальності «Фінанси і кредит», групи 2
Нефедова Ольга
Викладач: доцент кафедри фінансів
Подвисоцька Т. О.
Київ — 2014
Home Assignment #4
Assignment #1 (2 points)
State with brief reason whether the following statements are TRUE, FALSE or UNCERTAIN
In the presence of heteroscedasticity the usual OLS method always overestimates the standard errors of estimators.
FALSE, typically, but not always, will the variance be overestimated.
If multicollinearity is present, the conventional t and F tests are invalid.
TRUE, In the case of multicollinearity, our coefficients are biesed and unefficient (we have large variance). Thus, the confidance intervals tend to be much wider leading to the acceptance of the “zero null hypothesis” more readily. Also t ratio tends to be statistically insignificant.
If a regressor that has nonconstant variance is (incorrectly) omitted from a model, the OLS residuals will be heteroscedastic.
FALSE, heteroscedasticity is about the variance of the variance of the error term ui and not about the variance of the regressor.
If a regression model is mis-specified (e.g. an important variable is omitted), the OLS residuals will show a distinct pattern.
TRUE. See answer to 5 below.
If residuals estimated from an OLS regression exhibit a systematic pattern, it means heteroscedasticity is present in the data.
FALSE, besides heteroscedasticity such a pattern may result from autocorrelation, model specification errors etc.
In the presence of autocorrelation the conventionally computed variances and standard errors of forecast values are inefficient.
TRUE.
Since the forecast errors involves
,
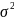which is incorrectly estimated by the usual OLS formula.
The exclusion of an important variable(s) from a regression model may give a significant d-value.
TRUE, a significant Durbin-Watson d could signify specification errors.
In the presence of autocorrelation OLS estimators are unbiased as well as inefficient.
TRUE, when autocorrelation is present, OLS estimators are unbiased and they are not efficient.
The R2 values of two models, one involving regression in the first-difference form and another in the level form, are not directly comparable.
TRUE. We can compare the models which have the same regressand.
In case of omitted variable in the regression, the estimates would be still unbiased, but inefficient.
FALSE, if an important variable is omitted the OLS estimates would be biased and inefficient.