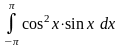- •Определители и системы
- •Матрицы
- •Произведение матриц .
- •Прямая в пространстве
- •Плоскость
- •VI. Линии на плоскости
- •Кривые второго порядка
- •VII. Пределы
- •VIII. Непрерывность и разрывы
- •IX. Вычисление производной
- •Вычислить , если ,
- •Вычислить , если
- •Вычислить , если
- •X. Приложения производной
- •Материальная точка движется по следующему закону, выражающему зависимость пути от времени: . Какова будет мгновенная скорость этой точки в момент времени .
- •XI. Неопределенный интеграл
- •Вычислить :
- •Вычислить :
- •Экзаменационные вопросы Математика 1
Материальная точка движется по следующему закону, выражающему зависимость пути от времени: . Какова будет мгновенная скорость этой точки в момент времени .
Материальная точка движется по следующему закону, выражающему зависимость пути от времени:
 .
Какова будет мгновенная скорость этой
точки в момент времени
.
Какова будет мгновенная скорость этой
точки в момент времени
 .
.
Материальная точка движется по следующему закону, выражающему зависимость пути от времени:
 .
Какова будет мгновенная скорость этой
точки в момент времени
.
Какова будет мгновенная скорость этой
точки в момент времени
 .
.Материальная точка движется по следующему закону, выражающему зависимость пути от времени: . Каково будет ускорение этой точки в момент времени
Материальная точка движется по следующему закону, выражающему зависимость пути от времени:
 .
Каково будет ускорение этой точки в
момент времени
.
.
Каково будет ускорение этой точки в
момент времени
.Материальная точка движется по следующему закону, выражающему зависимость пути от времени:
 .
Каково будет ускорение этой точки в
момент времени
.
.
Каково будет ускорение этой точки в
момент времени
.
XI. Неопределенный интеграл
Вычислить интеграл
 .
.Вычислить интеграл
 .
.Найти интегралы
 .
.Вычислить интеграл
 .
.Найти интеграл
 .
.Вычислить интеграл

Вычислить интеграл
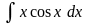 .
.Вычислить интеграл
 .
.Вычислить интеграл
 .
.Вычислить интеграл
 .
.
Вычислить интеграл
 :
:Вычислить интеграл
 :
:Вычислить интеграл
 :
:Вычислить интеграл
 :
:Вычислить интеграл
 :
:Вычислить интеграл
 :
:Вычислить интеграл
 :
:Вычислить интеграл
 :
:Вычислить интеграл
 :
:
Площадь фигуры, ограниченной линиями
 ,
, ,
, :
:
Найти площадь фигуры, ограниченной линиями

Найти площадь фигуры, ограниченной линиями
 :
:Вычислить объем тела, полученного от вращения вокруг оси ординат плоской фигуры, ограниченной линиями
 :
:
Площадь фигуры, ограниченной линиями
 ,
, :
:
Площадь фигуры, ограниченной кривой, заданной в полярных координатах:
Если линия задана уравнением в системе полярных координат: r=r(), и -значения полярного угла соответственно начала А и конца В дуги и ,то длина дуги вычисляется по формуле:
Вычислите несобственный интеграл
 :
:Вычислите несобственный интеграл
 :
:Вычислите несобственный интеграл
 :
:Пусть
 непрерывна на
непрерывна на .
Какое равенство выражает теорему о
среднем значении?
.
Какое равенство выражает теорему о
среднем значении?
Как вычисляется площадь поверхности, полученной вращением кривой
 ?
?
Вычислите несобственный интеграл :
Вычислите несобственный интеграл
 :
:Вычислить :
Вычислить :
Вычислить несобственный интеграл
 :
:
Экзаменационные вопросы Математика 1
Матрицы и операции над ними. Единичная, обратная, транспонированная, невырожденная матрица. Ранг матрицы.
Что такое базис пространства? Какие элементы называются линейно зависимыми?
Что есть алгебраическая проекция вектора? Что называется координатами вектора?
Определение скалярного произведения, коорд.форма.
Определение векторного произведения, коорд.форма.
Определение смешанного произведения, коорд.форма.
Необходимое и достаточное условие ортогональности векторов.
Необходимое и достаточное условие коллинеарности векторов.
Необходимое и достаточное условие компланарности векторов.
Геом. и физ. смысл произведений векторов.
Различные уравнения прямой на плоскости. Угол между прямыми. Условия параллельности и перпендикулярности прямых.
Различные уравнения плоскости(общее, неполные, в отрезках). Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.
Различные уравнения прямой в пространстве. Угол между прямыми. Условия параллельности и перпендикулярности прямых в пространстве.
Окружность, эллипс, гипербола, парабола и их канонические уравнения. Эксцентриситет, директриса, фокусы кривых 2-го порядка.
Числовая последовательность. Монотонная, ограниченная, сходящаяся. Бесконечно большая. Бесконечно малая.
Свойства сходящихся последовательностей. Свойства бесконечно малых последовательностей. Связь между бесконечно большими и бесконечно малыми величинами.
Теорема Вейерштрасса о существовании предела.
Функция и методы ее задания. Классификация функций.
Односторонние пределы. Замечательные пределы.
Непрерывность функции в точке и на отрезке. Точки разрыва и их классификация.
Производная и дифференциал функции. Производная основных элементарных функции. Геометрический и физический смысл производной. Уравнение касательной и нормали.
Дифференцируемость функции. Основные правила дифференцирования. Производная сложной, обратной, неявной функции.
Основные теоремы дифференциального исчисления (Ферма, Ролля, Лагранжа, Коши).
Исследование функции. Экстремум функции. Направление выпуклости графика функции. Точки перегиба и асимптоты. Общая схема исследования функции.
Первообразная и неопределенный интеграл, его основные свойства.
Таблица основных интегралов и основные методы интегрирования.
Определенный интеграл. Свойства.
Геометрические приложения определенного интеграла
Физические приложения определенного интеграла