Определители и системы

При каком значении система не имеет решения ?

Найти , если:

Найти значение из системы

Вычислить

Решите систему уравнений: .

Найти все решения системы .

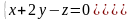Найдите минор элемента определителя .

Решите систему уравнений по формулам Крамера . Найдите х₁ + х₂.

Решите систему уравнений по формулам Крамера . Найдите х₁ + х₂.

Вычислите определитель 3-го порядка .

Минор элемента определителя равен:

Решите уравнение .

Матрицы

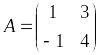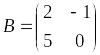
Найти элемент с₁₂ матрицы С = 2(А+В), есл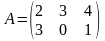и ,

и Найти произведение матриц.

Ранг матрицы равен…

Определить ранг матрицы .

Найти элемент матрицы , где , .

Найдите обратную матрицу к матрице .

Найдите матрицу M*N, если М= , N = .

Найдите матрицу 3M - 2N, если М= , N= .

Найдите обратную матрицу: M= .

Вычислите .

Вычислить , если

Произведение матриц .

Произведение матриц .

=?

Если 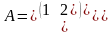, то -?

Алгебраическое дополнение к элементу в матрице .

Найти матрицу : , .

Вычислить матрицу, обратную к матрице .

ВЕКТОР

При каком значении параметра , векторы и будут перпендикулярны?

Пусть , , . Найти угол между векторами.

Найти угол, образованный вектором с осью .

Направляющие косинусы вектора , удовлетворяют условию…

Если вектора , найти вектор .

Вычислить площадь параллелограмма, построенного на векторах .

Найти скалярное произведение векторов 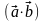, если .

Найти векторное произведение , если _.

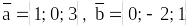Даны векторы 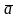(3;-2;6) и (-2;1;0). Найти координаты вектора 2 + З .

Найти смешанное произведение векторов .

Разложите вектор по векторам и .

Какое условие выполняется для векторов , , если они компланарны?

Найдите скалярное произведение векторов , .

Вычислить модуль вектора .

Сила приложена к точке О(1;2;1). Определить момент этой силы относительно точки А(-1:2:3).

Векторы некомпланарны. Будут ли коллинеарными векторы: ?

Прямая в пространстве

Задана прямая и плоскость . Как они расположены?

Составить канонические уравнения прямой, проходящей через точку М (2;0;-3) параллельно прямой .

Даны вершины треугольника АВС: А (3;6;-7), В (-5;2;3), С(4;-7;-2). Составить уравнение медианы ВМ.

Составить канонические уравнения прямой, проходящей через точку М (2;3;-5) перпендикулярной плоскости х + 3у – 2z + 7 = 0.

Показать параллельность прямых и .

Найти угол между прямыми и .

Составить канонические уравнения прямой, проходящей через точку М (2;-1;3) перпендикулярной плоскости 2х - 3у + 4z - 1 = 0.

Даны вершины треугольника АВС: А (3;-4;2), В (0;1;2), С (-5;2;4). Составить уравнение медианы АМ.

Составить канонические уравнения прямой, проходящей через (^.) А(-2;3;0) перпендикулярной плоскости 2х - 3у + 4z - 1 = 0.

Доказать параллельность прямых и .

Составить канонические уравнения прямой, проходящей через точку А (1;-1;2) параллельно оси Оу.

Найти угол между прямыми и .

Составить уравнение прямой, проходящей через точки М₁ (0;2;-3) и М₂ (-1;3;-4).

Написать уравнения прямой, проходящей через А (-3;0;4) перпендикулярной плоскости ХОУ.