Дисперсионный анализ

Цель дисперсионного анализа - оценка степени влияния факторов на выходные параметры (признаки). Задачи дисперсионного анализа:

• изучение совместной изменчивости признаков в зависимости от определяющих их факторов и установление причинно-следственных связей между ними;

• выбор наиболее важных факторов и оценка их влияния;

• установление причины явлений.

В основе дисперсионного анализа лежит закон сохранения изменчивости – ничего не меняется без причины. Согласно этому закону в дисперсионном анализе общая дисперсия разлагается на слагаемые, каждое из которых характеризует влияние того или иного фактора или их сочетания.

По результатам наблюдений формируется матрица исходных данных с учетом каждого регулирующего фактора, воздействующего на признак. Факторы являются внешними условиями, влияющими на эксперимент. По числу факторов дисперсионный анализ разделяется на однофакторный, двухфакторный и т.д. По количеству факторов и повторностей – на равномерно-пропорциональный и неравномерно-пропорциональный.

Исходными данными для дисперсионного анализа могут выступать результаты наблюдений – параметры (признаки), зависящие от действия различных, одновременно действующих факторов. Условия для проведения дисперсионного анализа:

• результаты наблюдений являются независимыми случайными величинами,

• случайные величины нормально распределены,

• случайные величины имеют близкие дисперсии.

В простейшем случае - при однофакторном дисперсионном анализе исходная матрица признаков состоит из столбцов – факторов и строк – повторностей :

Здесь - значение признака при -й повторности -го фактора.

Если анализируемый фактор влияет на признак, то влияние сказывается на величине групповых средних, которые будут существенно отличаться друг от друга. Целью дисперсионного анализа при этом будет проверка статистической значимости различия между средними. Проверка проводится с помощью разбиения общей дисперсии (суммы квадратов отклонений) на части:

, где

- межгрупповая изменчивость, часть общей изменчивости, связанная с действием контролирующих факторов. Эта изменчивость может объяснить различие между средними значениями в группах.

- внутригрупповая изменчивость, является результатом действия неучтенных, случайных факторов. При проведении эксперимента она не может быть предсказана или объяснена.

Суммы квадратов отклонений равны

C = - ,

,

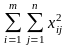где n – число факторов, m – число повторностей, N – объем выборки,

N .

Для определения доли влияния факторов и статистической значимости различия между групповыми средними определяются дисперсии.

Числа степеней свободы равны

.

Дисперсии – факторная (межгрупповая) ,

Остаточная (внутригрупповая ) .

Доли влияния факторов:

учтенного ;

неучтенного ;

.

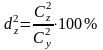Анализ статистической значимости различия между средними значениями проводится на основе полученных дисперсий. Перед проведением анализа выдвигается нулевая гипотеза – межгрупповые средние равны, дисперсии групповые и межгрупповые не различаются , никакого систематического действия факторов на результативный признак не существует и наблюдаемые различия между групповыми средними случайны.

Если критерий Фишера расчетный превышает критерий Фишера табличный: , различие между дисперсиями значимо, нулевая гипотеза отвергается и принимается гипотеза о существовании различия между средними.

В противном случае – когда нет оснований отвергать нулевую гипотезу.

Дисперсионный анализ в лесном хозяйстве может использоваться при изучении влияния удобрений, уходов, генотипа на рост посадочного материала при создании лесных культур.

Определение влияния фактора времени на радиальный прирост, определение доли влияния фактора, оценка его статистической значимости.

Однофакторный регрессионный анализ.

Регрессия – изменение функции в зависимости от изменения одного или нескольких аргументов (лат. regressio –движение назад). Корреляционную зависимость между признаками можно описать разными способами, любая форма связи может быть выражена уравнением общего вида , где - зависимая переменная или функция от независимой переменной (аргумента). Соответствие между функцией и аргументом может быть задано таблицей, графиком, формулой.

Регрессионный анализ необходим для определения формы связи между случайными величинами, тесноты связи. График регрессии позволяет получить наглядное представление о форме и тесноте корреляционных связей между признаками. Задача регрессионного анализа состоит в выражении корреляционной связи уравнением определенной функции, чтобы затем прогнозировать значения одной из случайных переменных по известным значениям другой.

Регрессионный анализ может быть:

- по числу независимых переменных (факторов) однофакторным и многофакторным,

- по форме графика линейным и нелинейным.

Для характеристики формы связи при изучении зависимостей используют уравнение регрессии (кривую регрессии). Уравнение регрессии – функция определенного класса, параметры которой находят методом наименьших квадратов по наблюдаемым значениям.

Однофакторный регрессионный анализ