Санкт-Петербургский Государственный Лесотехнический университет

Им. С.М. Кирова

кафедра лесной таксации, лесоустройства и геоинформационных систем

Отчёт по лабораторным работам

по дисциплине «Системный анализ и моделирование в лесном деле»

Выполнил: студентка ЛХФ 4к. 4 гр.

Мигунова Джулия Константиновна №зач. 501082

Проверил: доцент, к.с.–х.н.

Синкевич Антон Евгеньевич

Санкт-Петербург

2014г.

ОДНОМЕРНЫЙ АНАЛИЗ ДАННЫХ

Статистическая обработка данных.

Случайная величина – величина, которая в результате испытаний принимает то или иное возможное значение, заранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств. Случайная величина характеризует результат испытания количественно. Случайные величины могут быть дискретными и непрерывными. Если случайная величина принимает значения, выражающиеся только целыми числами, она является дискретной, если любые числовые значения – непрерывной.

Случайная величина в независимых повторных испытаниях может принимать различные значения – . Функция , связывающая значения случайной величины с ее вероятностями, называется законом распределения случайной величины, который можно выразить в виде вариационного ряда (таблицы) или кривой вероятности (графика). Вариационным рядом называется двойной ряд чисел, показывающий, каким образом значения случайной величины связаны с их повторяемостью.

Распределение вероятностей полностью характеризует случайную величину. Но на практике часто достаточно знать отдельные количественные показатели, характеризующие это распределение. К числовым характеристикам, позволяющим характеризовать распределение случайной величины, относят среднее арифметическое значение, медиану, моду, среднее геометрическое значение, дисперсию, среднее квадратическое отклонение, стандартную ошибку, минимальное и максимальное значение, ранги, квартили, коэффициенты асимметрии и эксцесса, коэффициент вариации и др.

Среднее арифметическое значение (Average¹) характеризует положение случайной величины на числовой оси, определяет центр распределения. Среднее значение показывает, какое значение принимает случайная величина в среднем с учетом вероятностей ее отдельных значений:

,

где - случайная величина, – объем выборки.

Для дискретных случайных величин среднее значение определяется по формуле:

,

где – вероятность того, что случайная величина примет значение .

Медиана (Median) – значение случайной величины, относительно которой ряд распределения делится на две половины: в обе стороны от медианы располагается одинаковое число членов ряда. Геометрически – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам. Для вычисления медианы выборка упорядочивается в порядке возрастания. Определяется медианный интервал - интервал, в котором будет находиться медиана - складываются частоты ряда от меньших к большим до величины _, превосходящей половину членов ряда . Медиана вычисляется по формуле:

,

где - нижняя граница медианного интервала, - величина классового интервала, - число членов ряда, - число накопленных частот, стоящих до медианного класса, – частота медианного класса.

Мода (Mode) - значение случайной величины, соответствующее максимальной плотности распределения. Это величина, которая встречается наиболее часто. Геометрически – абсцисса точки максимума кривой распределения.

,

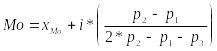где - нижняя граница модального интервала (интервала с наибольшей частотой – ), - частота класса, предшествующего модальному, – частота класса, следующего за модальным, - величина классового интервала.

Среднее геометрическое значение (Geo. Mean) используется для определения среднего значения прироста явления (объекта) за разные периоды времени, например, радиальный прирост древесины, количество подроста на пробных площадках. Прирост за каждый период должен при этом выражаться в процентах или долях единицы.

Дисперсия 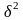(Variance) и среднее квадратическое отклонение (Standart deviation) характеризуют меру рассеяния случайной величины, относительно средней. Дисперсия является основным показателем разнообразия значений признака в группе. Иные показатели разнообразия – максимальное, минимальное и среднее значения признака могут характеризовать разнообразие признака в общем виде, без учета колебаний его значений, относительно среднего. Так в двух выборках с одинаковыми лимитами и средними значениями возможно разное распределение случайных величин. Дисперсия измеряется в тех же величинах, что и изучаемая случайная величина, но возведенных в квадрат. Среднее квадратическое отклонение  по смыслу равнозначно дисперсии, но выражается в тех же единицах, что и сама анализируемая величина, в данном случае в метрах.

Дисперсия определяется по формуле:

.

Среднее квадратическое отклонение для нормального распределения определяется по формуле:

.

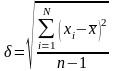Дисперсия и среднее квадратическое отклонение могут принимать значения от нуля до бесконечности. В случае, если варьирование случайной величины внутри выборки незначительно, дисперсия будет близка к нулю (например, диаметр на высоте груди в чистом сосняке 65 лет). Если случайная величина в выборке будет часто и существенно отклоняться от среднего, дисперсия будет расти (диаметр на высоте груди в еловом выделе с двумя поколениями – 65 и 120 лет).

Стандартная ошибка (Std. Error) характеризует отклонение случайной величины от среднего арифметического значения в выборке. Зависит от среднего квадратического отклонения и размера выборки.

.

Минимальное (min) и максимальное значение (max) определяют точные пределы колебаний случайной величины в выборке. Средняя величина недостаточно характеризует случайную величину. При одинаковых значениях средних в разных выборках характеризуемые ими случайные величины могут значительно отличаться. Поэтому для более полной характеристики вариационного ряда вычисляются максимальное и минимальное значения случайной величины, между которыми распределяются все члены данной совокупности.

Размах R (Range) характеризует варьирование признаков, как разницу между максимальным и минимальным значением:

.

Квартили – значения случайных величин, отсекающие на графике ¼ часть ряда. Нижний квартиль (Lower quartile) содержит 25% значений случайных величин. Верхний квартиль (Upper quartile) содержит 75% значений случайных величин. Квартили, мода и медиана характеризуют структуру вариационного ряда.

Квартильный размах (Interquartile Range) равен разности значений верхней и нижней квартили, содержит 50% наблюдений, вокруг медианы.

Коэффициент асимметрии (Skewness) характеризует форму вершины кривой распределения (скошенность). Если этот коэффициент отчетливо отличается от 0, распределение является  асимметричным. Положительная асимметрия свидетельствует об отклонении кривой влево, отрицательная – вправо, относительно центра распределения.

,

где - частота встречаемости значений (например, деревьев одинаковой ступени толщины). Ошибка асимметрии определяется по формуле:

.

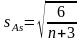Коэффициент эксцесса (Kurtosis) также характеризует форму вершины кривой распределения. Положительный эксцесс наблюдается у кривых с заостренной вершиной, отрицательный – для кривых с притупленной вершиной относительно кривой нормального распределения.

Ошибка эксцесса определяется по формуле:

.

Стандартизированные коэффициенты асимметрии и эксцесса 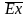(Stnd. Skewness и Stnd. Kurtosis) позволяют оценивать близость распределения случайной величины к нормальному. Определяются делением значений коэффициентов асимметрии и эксцесса на их ошибки:

При больших объемах выборки стандартизированные коэффициенты близки к натуральным. При небольших выборках, отклонения стандартизированных коэффициентов асимметрии и эксцесса за пределы интервала от –2.0 до 2.0 указывают на несоответствие изучаемого распределения нормальному.

Коэффициент вариации (Coeff. of variation) используется для сравнения изменчивости признаков, выраженных разными единицами. Представляет собой процентное отношение среднего квадратического отклонения к среднему арифметическому:

.

Закон нормального распределения

Плотность распределения нормального вида для случайной величины определяется по формуле:

.

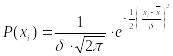где - стандартное отклонение случайной величины от среднего значения . В показатель степени входит нормированное отклонение .

Значения t определяемые на основе среднего и среднеквадратического отклонения приводятся в специальных таблицах. Вероятность отклонения любого xi от центра распределения x, где , определяется функцией нормированного отклонения t. Графически эта функция выражается в виде кривой вероятности, называемой нормальной кривой. Положение этой кривой строго определяется двумя параметрами – средней величиной и стандартным отклонением. При большой величине стандартного отклонения форма нормальной кривой может приближаться к пологой. Во всех случаях нормальная кривая строго симметрична относительно центра распределения и сохраняет правильную колоколообразную форму.

Основные свойства нормального распределения. Для нормального распределения абсолютные значения среднего, моды и медианы равны, асимметрия и эксцесс отсутствуют. На равные интервалы от центра распределения, измеряемые нормированным отклонением, приходится равное число наблюдений. Вероятность любого значения случайной величины отклониться от средней на t, 2t, 3t равна:

P ( | xi – x| < t) = 0.6827

P ( | xi – x| < 2t) = 0.9545

P ( | xi – x| < 3t) = 0.9973

Следовательно, с вероятностью P=0.6827 можно утверждать, что наугад отобранное значение нормально распределенной случайной величины не выйдет за пределы от до . Для нормального распределения 68% стандартизированных значений случайных величин будут находиться в пределах от , 95% в пределах и 99% в пределах .

При обработке опытных данных с помощью STATGRAPHICS Plus для получения оптимальных результатов необходимо, чтобы анализируемые случайные величины имели распределение близкое к нормальному. Критериями нормальности распределения могут являться - близость значений моды, медианы, средней величины между собой, значения стандартизированных коэффициентов асимметрии и эксцесса в пределах 2 (по модулю).

Близость распределения нормальному можно оценивать следующими способами: по стандартизированным коэффициентам асимметрии и эксцесса, сравнением теоретических частот с эмпирическими по критериям соответствия.

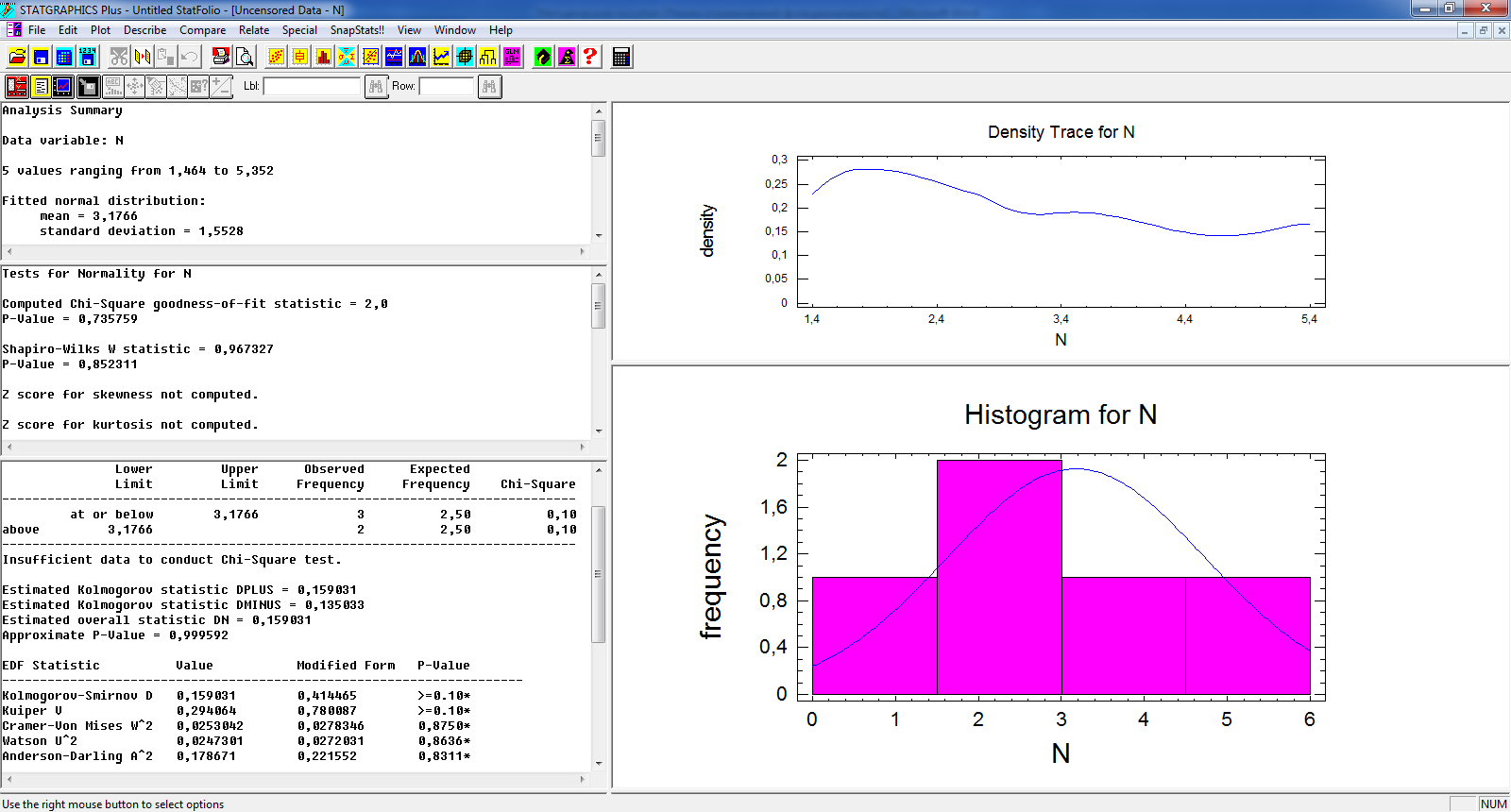
Пример 1. Определение числовых характеристик таксационных показателей пробной площади. Оценка близости их распределения к нормальному.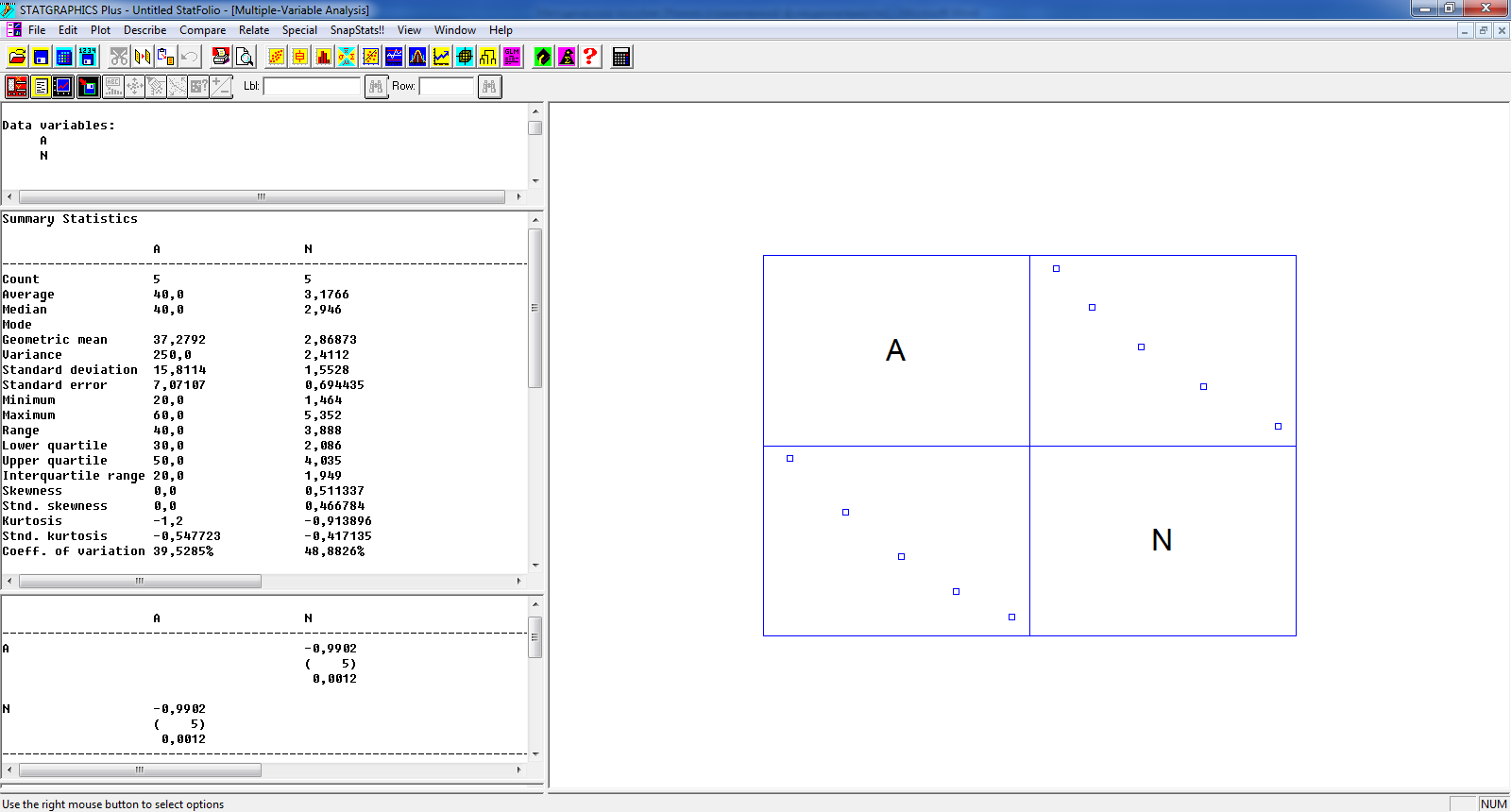

Пример 2.